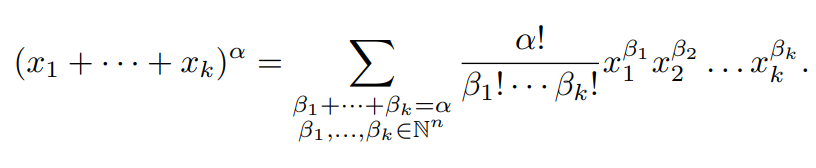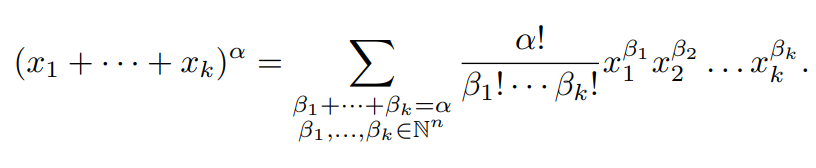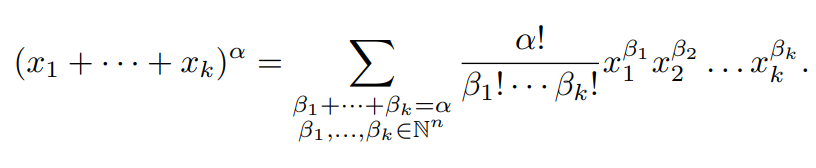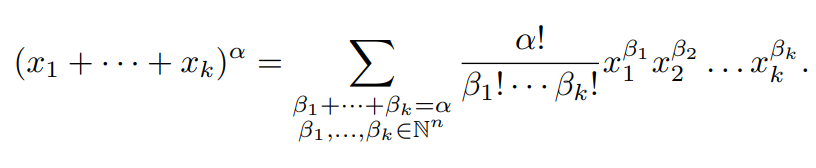STEM版,合并数学,物理,化学,科学,工程,机械。不包括生物、医学相关,和计算机相关内容。
版主: verdelite, TheMatrix
-
molen(猛犸象)楼主
- 论坛元老

- 帖子互动: 419
- 帖子: 14491
- 注册时间: 2023年 3月 2日 16:52
帖子
由 molen(猛犸象)楼主 »
再请您看看这个问题,其中 alpha, beta 都是 multi-index notation,这个使用了multi-index notation的 multinomial expansion 如何证明?
思路?或者参考?
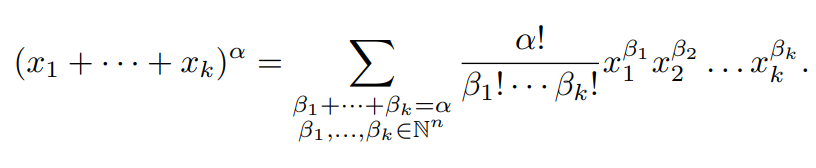
x1

标签/Tags:
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1302
- 帖子: 14133
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
这个就是排列组合问题。先把k=2的情形(既二元多项式展开)弄清楚了,一般k的情况是一样的道理。
具体地说,就是k种颜色的球(每种颜色的球都有足够多个,大于等于alpha即可)混在一起,你从中取出alpha个球,按顺序排列。问:有多少种排列含有beta_1个第一种颜色球,beta_2个第二种颜色球,...,beta_k个第k种颜色球。答案就是上面公式里的那个分数式。这个数正好对应图中展开式的系数。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
YWY 写了: 2023年 7月 13日 21:47
这个就是排列组合问题。先把k=2的情形(既二元多项式展开)弄清楚了,一般k的情况是一样的道理。
具体地说,就是k种颜色的球(每种颜色的球都有足够多个,大于等于alpha即可)混在一起,你从中取出alpha个球,按顺序排列。问:有多少种排列含有beta_1个第一种颜色球,beta_2个第二种颜色球,...,beta_k个第k种颜色球。答案就是上面公式里的那个分数式。这个数正好对应图中展开式的系数。
alpha不是一个数,是一个整数向量。
我查了一下。multi index有点意思。这里的x
1,…x
k都是向量,用multi index power一下就变成了数。整个公式形式上完全就是数的multi nominal公式。很巧妙。
-
(ツ)(污坛忍者)
- 知名作家

- 帖子互动: 54
- 帖子: 1091
- 注册时间: 2023年 6月 2日 12:38
帖子
由 (ツ)(污坛忍者) »
盲猜一个对k用归纳法
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1302
- 帖子: 14133
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
TheMatrix 写了: 2023年 7月 13日 22:58
alpha不是一个数,是一个整数向量。
我查了一下。multi index有点意思。这里的x
1,…x
k都是向量,用multi index power一下就变成了数。整个公式形式上完全就是数的multi nominal公式。很巧妙。
好的,学习了。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1302
- 帖子: 14133
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
molen 写了: 2023年 7月 13日 21:14
再请您看看这个问题,其中 alpha, beta 都是 multi-index notation,这个使用了multi-index notation的 multinomial expansion 如何证明?
思路?或者参考?
如果承认我二楼说的(非向量)展开式,那么一楼的展开式,通过定义用非向量的形式算两边,然后对比,就能看出是相同的。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
molen 写了: 2023年 7月 13日 21:14
再请您看看这个问题,其中 alpha, beta 都是 multi-index notation,这个使用了multi-index notation的 multinomial expansion 如何证明?
思路?或者参考?
我先把左边按定义展开,设向量维度为n:
(x
1+...+x
k)
α
=(x
11+...+x
k1)
α1 *(x
12+...+x
k2)
α2... *(x
1n+...+x
kn)
αn
然后咋办?
-
molen(猛犸象)楼主
- 论坛元老

- 帖子互动: 419
- 帖子: 14491
- 注册时间: 2023年 3月 2日 16:52
帖子
由 molen(猛犸象)楼主 »
TheMatrix 写了: 2023年 7月 14日 10:58
我先把左边按定义展开,设向量维度为n:
(x
1+...+x
k)
α
=(x
11+...+x
k1)
α1 *(x
12+...+x
k2)
α2... *(x
1n+...+x
kn)
αn
然后咋办?
应该就是这样,第一步之后,先求
(x
1+...+x
k)
α
用归纳法,然后在把全部乘到一起去,用multi-index的一些符号缩写来简洁化
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1302
- 帖子: 14133
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
YWY 写了: 2023年 7月 14日 00:24
如果承认我二楼说的(非向量)展开式,那么一楼的展开式,通过定义用非向量的形式算两边,然后对比,就能看出是相同的。
TheMatrix 写了: 2023年 7月 14日 10:58
我先把左边按定义展开,设向量维度为n:
(x
1+...+x
k)
α
=(x
11+...+x
k1)
α1 *(x
12+...+x
k2)
α2... *(x
1n+...+x
kn)
αn
然后咋办?
每一项因式都可以继续用(我二楼提的)公式展开。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
YWY 写了: 2023年 7月 14日 13:14
每一项因式都可以继续用(我二楼提的)公式展开。
tracking index,这个应该可以用computer algebra来做一下。
-
(ツ)(污坛忍者)
- 知名作家

- 帖子互动: 54
- 帖子: 1091
- 注册时间: 2023年 6月 2日 12:38
帖子
由 (ツ)(污坛忍者) »
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
(ツ) 写了: 2023年 7月 15日 00:40

嗯。不错。
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
YWY 写了: 2023年 7月 14日 13:14
每一项因式都可以继续用(我二楼提的)公式展开。
这里有一个对n-dim向量α做k-partition的总数问题。看到它等于对每一个α分量做k-partition,得到n个集合,然后n个集合的product集合。其余的都是index tracking。
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1302
- 帖子: 14133
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
TheMatrix 写了: 2023年 7月 15日 16:18
这里有一个对n-dim向量α做k-partition的总数问题。看到它等于对每一个α分量做k-partition,得到n个集合,然后n个集合的product集合。其余的都是index tracking。
是的,对n-dim向量α做k-partition,等价于对每个分量做k-partition(相对独立,乘积原理)。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1302
- 帖子: 14133
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
(ツ) 写了: 2023年 7月 15日 00:40

严格来说,这个推导并没有证明k=2的情况。所以还需直接(或间接)验证k=2的情况;或者在第一步说k=1和k=2都“显然”成立。但我觉得k=2的难度和k>=2的难度相当,你给的归纳推导也很大程度上基于k=2的情形。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
(ツ)(污坛忍者)
- 知名作家

- 帖子互动: 54
- 帖子: 1091
- 注册时间: 2023年 6月 2日 12:38
帖子
由 (ツ)(污坛忍者) »
YWY 写了: 2023年 7月 16日 01:38
严格来说,这个推导并没有证明k=2的情况。所以还需直接(或间接)验证k=2的情况;或者在第一步说k=1和k=2都“显然”成立。但我觉得k=2的难度和k>=2的难度相当,你给的归纳推导也很大程度上基于k=2的情形。
你说得对,k=2缺证明
-
(ツ)(污坛忍者)
- 知名作家

- 帖子互动: 54
- 帖子: 1091
- 注册时间: 2023年 6月 2日 12:38
帖子
由 (ツ)(污坛忍者) »
(ツ) 写了: 2023年 7月 16日 02:27
你说得对,k=2缺证明
补上k = 2的情形
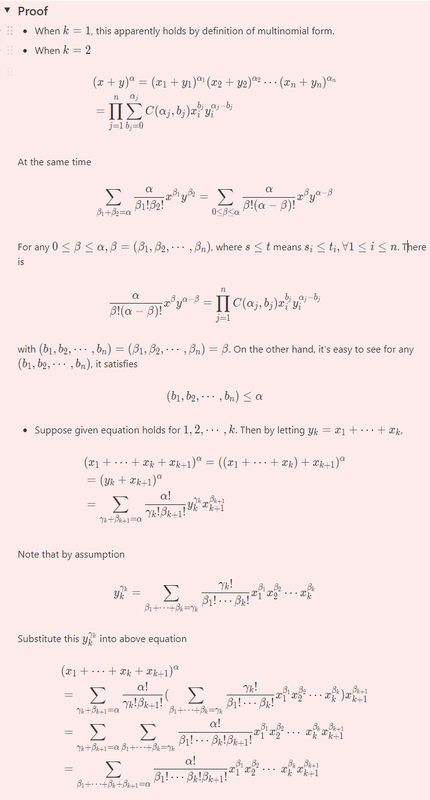
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1302
- 帖子: 14133
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
(ツ) 写了: 2023年 7月 16日 02:44
补上k = 2的情形
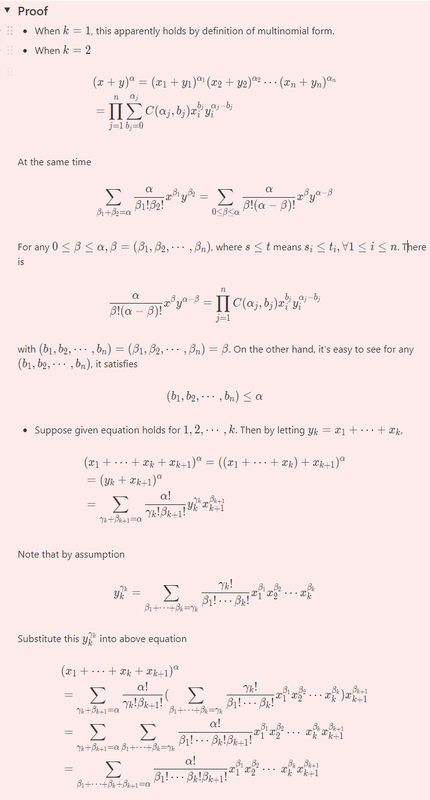
赞!
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
MrAnderson
- 论坛精英

- 帖子互动: 226
- 帖子: 7516
- 注册时间: 2022年 7月 23日 11:57
帖子
由 MrAnderson »
induction
molen 写了: 2023年 7月 13日 21:14
再请您看看这个问题,其中 alpha, beta 都是 multi-index notation,这个使用了multi-index notation的 multinomial expansion 如何证明?
思路?或者参考?
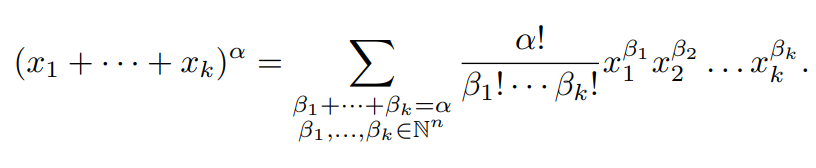
逼将有三种:老逼将,小逼将,装逼将
消灭买办是唯一出路
所谓女性解放,就是人类走向灭亡的开端
哈,狗子急了