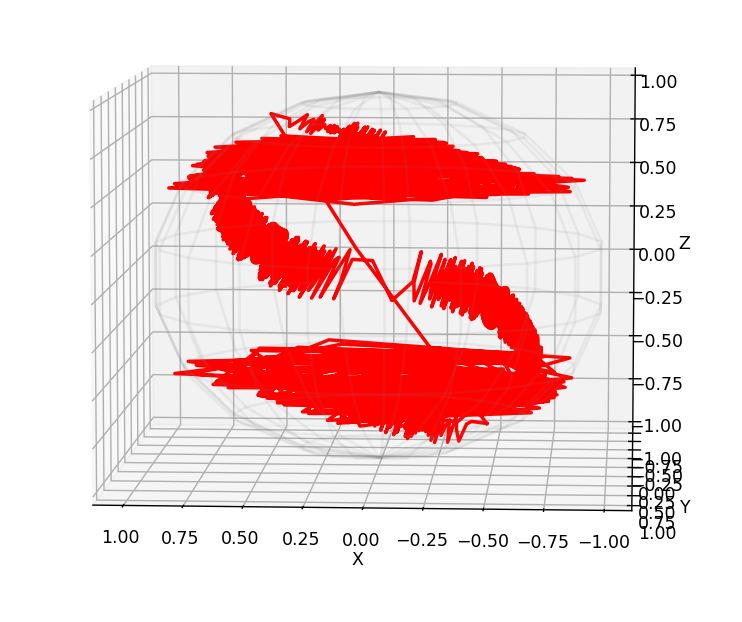
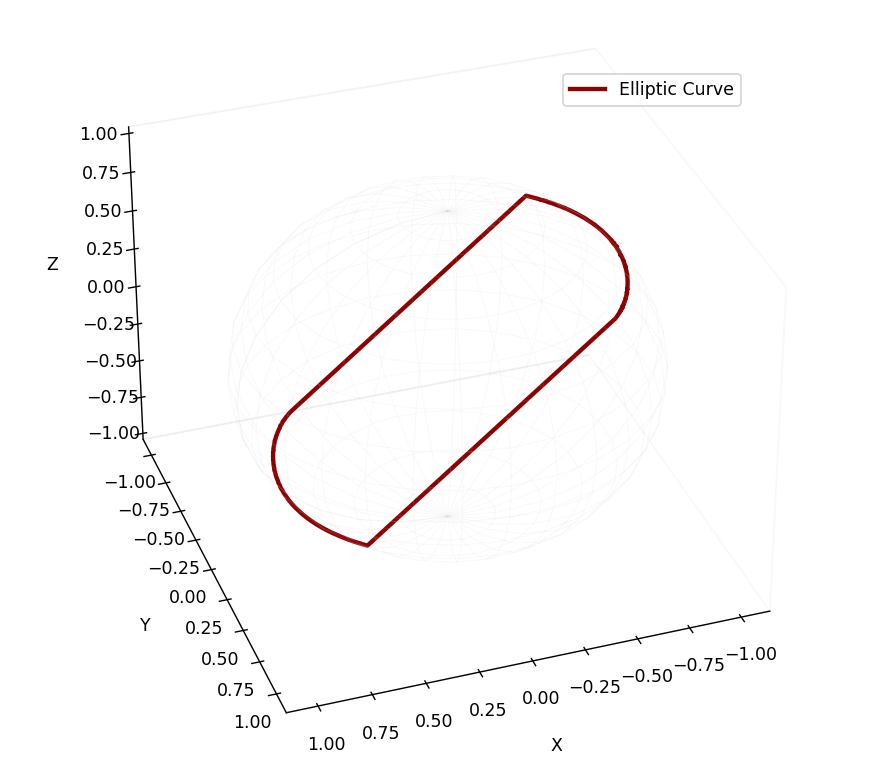
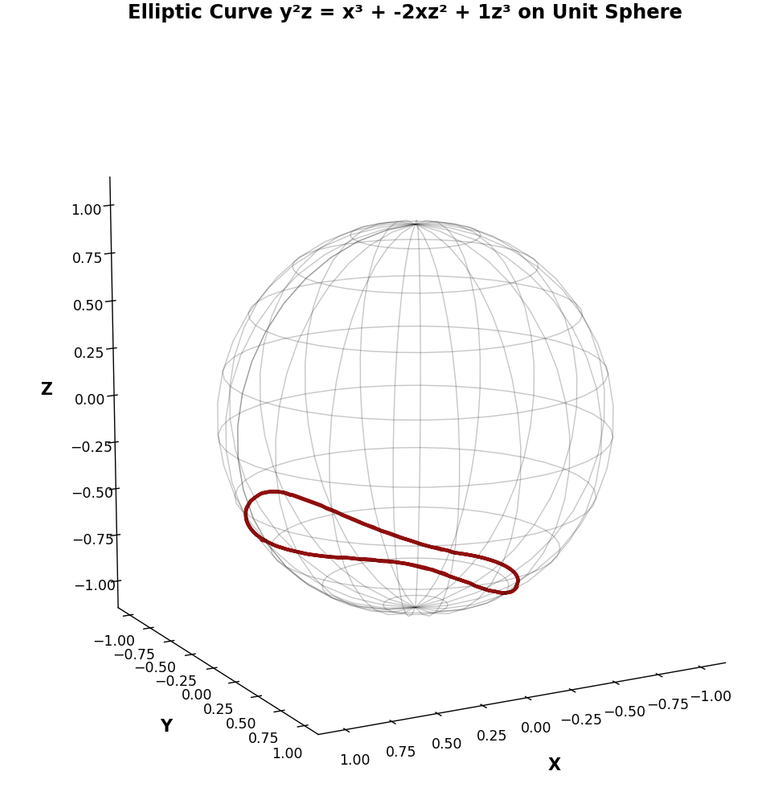
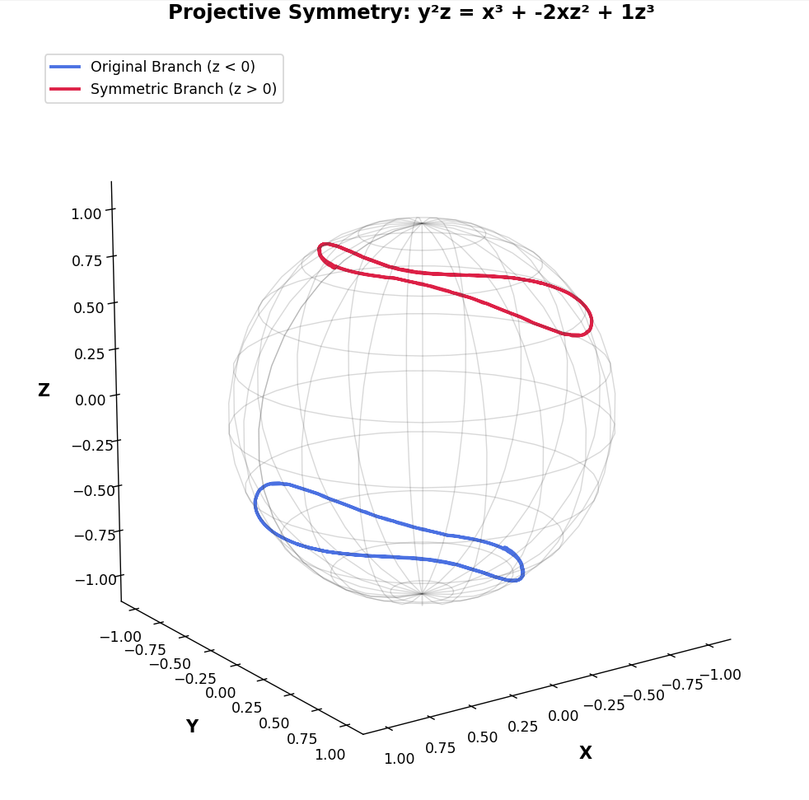
再试了一下用DeepThink(R1),也就是DeepSeek-R1。
它的思考过程确实impressive:
给回我的code是用角度做参数的。这是对的。这样才能smooth。Okay, the user wants a smooth curve for visualizing the intersection of an elliptic curve and a unit sphere in projective space using Python. They previously got a scatter plot and then an improved version using scipy.optimize and spline interpolation, but the assistant mistakenly mentioned R, so they clarified to use Python.
First, I need to ensure the code uses Python and produces a smooth curve. The scatter plot approach isn't smooth, so the solution should involve precise computation of intersection points and interpolation.
The main challenge is solving the system of equations accurately. The elliptic curve's homogeneous equation is y²z = x³ + axz² + bz³, and the unit sphere is x² + y² + z² = 1. Solving these simultaneously for points in 3D space can be tricky.
In the previous response, the assistant used scipy.optimize.root for each z-value. However, this might not capture all points, especially if the initial guess isn't good. Maybe a parametric approach could work better. For instance, parameterizing the sphere using spherical coordinates (theta, phi) and then solving for points that satisfy the elliptic curve equation.
Wait, spherical coordinates might complicate things because the elliptic curve equation isn't straightforward in those terms. Alternatively, we can use a meshgrid and compute the intersection more densely, then extract isosurfaces. But that's computationally intensive and might not give a smooth result.
Another idea: use contour3D to find the intersection. The intersection is where both equations equal zero. Using marching cubes algorithm (like in skimage's measure.marching_cubes) could extract the isosurface. But implementing that might require more steps.
Alternatively, using sympy to solve symbolically, but that's not feasible for complex equations. So numerical methods are better.
Wait, the user wants a smooth curve. The previous approach with solving for each z and interpolating with spline could work if enough points are found. The problem might be that the initial guesses for the root solver are not leading to convergence for all z-values. So maybe adjusting the initial guesses or the range of z-values could help.
Also, maybe the elliptic curve intersects the sphere in multiple disconnected components, so the solver needs to find all branches. But that's more complex. For simplicity, assume the intersection is a single continuous curve.
So, to make the curve smooth, increase the number of z-values sampled, use better initial guesses, and apply spline interpolation. Also, ensure the points are ordered correctly for interpolation.
Wait, the initial guess in the previous code was [0.5, 0.5] for x and y. Depending on the actual intersection points, this might not always converge. Maybe a better initial guess can be derived from the sphere's equation. For example, for a given z, x and y lie on the sphere x² + y² = 1 - z². So, parametrize theta to set x = sqrt(1 - z²) * cos(theta), y = sqrt(1 - z²) * sin(theta), and then solve for theta and z such that the elliptic curve equation holds. But this might complicate the root finding.
Alternatively, loop over possible angles theta and solve for z. Hmm, but how to parameterize it.
Alternatively, use a continuation method: start from a known point on the intersection and trace the curve by moving in the tangent direction, solving for the next point step by step. This is more involved but can produce a smooth, continuous curve. Implementing this would require more advanced numerical methods, which might be beyond the user's current setup.
Given time constraints, perhaps the best approach is to refine the existing method by:
1. Using a more adaptive initial guess based on the sphere's equation. For each z, compute possible x and y on the sphere and use those as initial guesses.
2. Increasing the number of z-values to sample, but perhaps focusing on the range where solutions exist. For example, if the sphere is unit, z ranges from -1 to 1. But not all z in that range may have solutions. Need to check where the elliptic curve intersects the sphere.
Alternatively, parameterize using a different variable, like theta, to traverse around the sphere and find corresponding points.
But maybe the initial approach can be adjusted. Let's see: in the previous code, for each z in np.linspace(-1, 1, 100), they solve for x and y. The initial guess is [0.5, 0.5], which might not be suitable for all z. For example, when z is close to 1, x and y are near zero, so the initial guess of 0.5 might be off. So adjusting the initial guess to be closer to sqrt(1 - z²) in some direction might help.
So, modifying the initial guess to be [sqrt(1 - z²), 0] or something similar. Let's try that. For each z, set initial x guess as sqrt(1 - z²) and y as 0. Then solve. If that converges, great. If not, try other angles.
But handling all angles is complex. Alternatively, use multiple initial guesses for each z. But that would increase computation time.
Alternatively, use the previous solution but adjust the initial guess dynamically. For example, after finding a point for z_i, use that x and y as the initial guess for z_{i+1}. This way, the solver follows the curve as z changes incrementally.
This is a form of continuation method. It assumes the curve is continuous and slowly varying with z. So, starting from a known point, increment z slightly and use the previous solution as the initial guess for the next step. This can help track the curve smoothly.
Implementing this would require:
1. Finding an initial point on the intersection.
2. Then, iterating over small steps in z, using the previous x and y as initial guesses.
But how to handle increasing and decreasing z? Maybe split into two directions from the initial point.
Alternatively, use a parameterization that allows stepping along the curve.
This approach would likely yield a more connected and smooth set of points, which can then be interpolated with a spline.
So, integrating this into the code:
- Find an initial point (z0, x0, y0) using a good initial guess.
- Then, vary z in small steps around z0, using the previous x and y as the new initial guesses.
- Collect all points and sort them to ensure ordering.
This could work better than the previous method of guessing for each z independently.
Another thing to note is that the elliptic curve in projective space might have points at infinity when z=0. But since we're intersecting with the unit sphere, z=0 would imply x² + y² = 1, but substituting z=0 into the elliptic curve equation gives y²*0 = x³ + 0 +0 → 0 = x³. So x=0, which combined with z=0 would require y²=1, so y=±1. But x=0, z=0, y=±1 are points (0, ±1, 0) in projective coordinates. However, these are points at infinity. The unit sphere equation in affine coordinates would not include these since z=0. But in projective space, points are equivalence classes. However, the visualization is in 3D space, so including z=0 might not contribute to the intersection except at those specific points. But maybe the intersection curve doesn't include those points.
In any case, focusing on z values where solutions exist is key. So, the code needs to handle z ranges where the equations have real solutions.
Putting this together, the revised approach would:
1. Find a starting point (x0, y0, z0) where the equations intersect.
2. Then, increment z in small steps, using previous (x, y) as initial guesses to track the curve.
3. Collect these points and interpolate with a spline.
This should give a smooth curve.
In the code, I can implement this by first finding a valid initial point, then marching along z in both positive and negative directions from there, updating the initial guesses each step.
But how to find the initial point? Maybe using a coarse grid search to find a z where solutions exist.
Alternatively, use the previous method but with smarter initial guesses.
Let me adjust the find_intersection function to use better initial guesses. For a given z, x and y must satisfy x² + y² = 1 - z². So, set x_guess = sqrt(1 - z²), y_guess = 0. If that doesn't work, try other angles. But this could get complex.
Alternatively, use a multi-start approach with several initial guesses for each z. But that's computationally expensive.
Alternatively, note that for the elliptic curve equation y²z = x³ + a x z² + b z³. For the sphere x² + y² + z² =1. Let's substitute y² from the sphere equation into the elliptic curve equation.
From the sphere: y² = 1 - x² - z².
Substitute into elliptic curve equation: (1 - x² - z²) z = x³ + a x z² + b z³.
Rearranged: x³ + a x z² + b z³ + x² z + z^3 - z =0.
But this is a cubic equation in x for fixed z. So for each z, solve this cubic equation to find x, then compute y from the sphere equation.
This might be a better approach. Because solving a cubic equation is more straightforward and can find all real roots.
So, for each z, solve the cubic equation for x, then compute y as sqrt(1 - x² - z²). Then check if the elliptic curve equation is satisfied.
Wait, substituting y² from the sphere equation into the elliptic curve equation gives:
y² z = x³ + a x z² + b z³
But y² = 1 - x² - z², so:
(1 - x² - z²) z = x³ + a x z² + b z³
Rearranged:
x³ + a x z² + b z³ + x² z + z³ - z = 0
Combine like terms:
x³ + a x z² + x² z + (b z³ + z³ - z) =0
x³ + x² z + a x z² + z³ (b +1) - z =0
This is a cubic equation in x, which can have up to three real roots. For each z in [-1, 1], solve this cubic equation for x, then compute y from y² =1 -x² -z².
This approach could be more efficient, as solving a cubic equation is manageable.
In Python, we can use numpy's roots function to find the roots of the cubic equation.
So here's the plan:
1. For each z in a range (say, between -1 and 1), compute the coefficients of the cubic equation in x.
2. Solve the cubic equation to find real roots for x.
3. For each real x root, compute y as ±sqrt(1 - x² - z²), ensuring the argument is non-negative.
4. Collect all valid (x, y, z) points.
5. Sort these points to form a continuous curve.
6. Use spline interpolation to create a smooth curve.
This approach avoids relying on initial guesses for the root solver and systematically finds all possible roots.
Let's outline the steps in code:
- Loop over z values from -1 to 1.
- For each z, compute the cubic equation coefficients.
- Solve the cubic equation using np.roots.
- Filter real roots.
- For each real x, compute y and check if y is real.
- Collect all valid points.
- Sort the points (perhaps by angle around some axis to ensure order).
- Interpolate with a spline.
This should give a smooth curve with all possible branches.
Implementing this:
First, define the cubic equation coefficients for each z.
The cubic equation is:
x³ + (z) x² + (a z²) x + [ (b +1) z³ - z ] = 0
So coefficients are [1, z, a*z², (b+1)*z³ - z]
For each z, compute these coefficients, then find roots.
Then, for each real root x, compute y² =1 -x² -z². If y² >=0, then y=±sqrt(y²).
But we need to verify if these x and y satisfy the original elliptic curve equation. Because substituting back, sometimes due to numerical errors, this might not hold exactly. But since we derived the cubic equation by substitution, the solutions should satisfy both equations, provided y² is correctly computed.
But let's test this.
Once the points are collected, they can be sorted. However, the cubic equation may yield multiple x values per z, leading to multiple branches. To plot them as separate curves, we need to group the points into branches.
But for simplicity, maybe the elliptic curve intersects the sphere in a single connected component, so all points can be ordered in a single sequence.
Alternatively, the intersection may have multiple loops. Sorting the points properly is key.
Assuming the curve is a single loop, sorting the points by an angular parameter (like the angle in the x-z plane) could help in ordering.
Alternatively, after collecting all points, use a nearest-neighbor approach to sort them in 3D space.
But this can get complex. An alternative is to parameterize the curve by z and for each z, collect x and y, then plot. However, if for some z there are multiple x and y, the plot may jump between branches.
Given that the user wants a smooth curve, perhaps focusing on the main branch where the elliptic curve and sphere intersect.
Alternatively, the initial code's approach of using a root solver with continuation (using previous solutions as initial guesses) may track a single branch smoothly.
Combining both methods: solving the cubic equation to get all possible points, then sorting them appropriately.
But let's proceed with implementing the cubic equation approach.
Here's the code:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.interpolate import splprep, splev
a = -1
b = 1
# Generate z values from -1 to 1
z_values = np.linspace(-1, 1, 400)
points = []
for z in z_values:
# Coefficients of the cubic equation: x^3 + c2 x^2 + c1 x + c0 =0
c3 = 1
c2 = z
c1 = a * z**2
c0 = (b +1)*z**3 - z
# Solve cubic equation
roots = np.roots([c3, c2, c1, c0])
# Filter real roots
real_roots = roots[np.isreal(roots)].real
for x in real_roots:
# Compute y^2
y_sq = 1 - x**2 - z**2
if y_sq >= 0:
y = np.sqrt(y_sq)
points.append([x, y, z])
points.append([x, -y, z]) # Add negative y
# Convert to numpy array
points = np.array(points)
# Check if any points were found
if len(points) ==0:
print("No intersection points found.")
else:
# Sort points by z, then x, then y to group them
# This might not work perfectly; need a better sorting strategy
# Alternatively, use principal component analysis to order points
# For simplicity, sort by z, then angle in x-y plane
# Compute angles
angles = np.arctan2(points[:,1], points[:,0])
# Sort by z, then angle
sorted_indices = np.lexsort((angles, points[:,2]))
sorted_points = points[sorted_indices]
# Spline interpolation
tck, u = splprep([sorted_points[:,0], sorted_points[:,1], sorted_points[:,2]], s=0.1)
u_new = np.linspace(0, 1, 1000)
x_new, y_new, z_new = splev(u_new, tck)
# Plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x_new, y_new, z_new, 'r-', lw=2, label='Intersection Curve')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Smooth Intersection Curve')
plt.show()
This code first solves the cubic equation for x at each z, computes y, and collects all valid points. Then it sorts them by z and angle to attempt ordering. However, the sorting might not be perfect, leading to a jagged curve. Increasing the number of z samples (e.g., 400) helps, but the spline's smoothing parameter (s=0.1) can be adjusted.
Potential issues:
- Multiple roots per z leading to disjoint branches. The current sorting might mix these, causing the spline to jump between branches.
- The angle calculation (arctan2(y, x)) sorts points around the origin, which may not correspond to the actual curve's topology.
Alternative sorting approach: using traveling salesman problem (TSP) to order points by proximity in 3D space. But that's computationally intensive.
Alternatively, using a nearest neighbor approach: starting from a point, find the nearest next point, and so on. This can be implemented but requires more code.
Given time constraints, perhaps the cubic equation method with improved sorting is the way to go. If the curve is a single continuous loop, sorting by z and then angle may work. If there are multiple loops, the code may need to separate them.
But the user's main request is for a smooth curve. Even with some imperfections, this approach should produce a smoother result than the scatter plot.
Testing the code with a= -1, b=1, the intersection curve should be a closed loop. However, depending on the elliptic curve's shape, the intersection with the sphere may vary. If the code collects enough points and sorts them properly, the spline interpolation should create a smooth curve.
Another consideration: the cubic equation might have no real roots for certain z values. For example, if z is such that the cubic has no real solutions, those z values are skipped. This could lead to gaps in the curve. But with a dense enough sampling of z, gaps can be minimized.
In conclusion, the code above should generate a smooth curve by solving the cubic equation for each z, collecting all valid points, sorting them, and applying spline interpolation. This approach avoids reliance on initial guesses and systematically finds all possible intersection points, leading to a smoother visualization.
代码: 全选
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.interpolate import splprep, splev
# Elliptic curve parameters
a = -1
b = 1
a,b = -2,1
# Generate z values
z_values = np.linspace(-1, 1, 400)
points = []
for z in z_values:
# Cubic equation coefficients: x³ + zx² + (a z²)x + [(b+1)z³ - z] = 0
coefficients = [1, z, a*z**2, (b+1)*z**3 - z]
# Solve cubic equation
roots = np.roots(coefficients)
real_roots = roots[np.isreal(roots)].real
for x in real_roots:
y_sq = 1 - x**2 - z**2
if y_sq >= 1e-6: # Account for floating point errors
y = np.sqrt(y_sq)
points.extend([[x, y, z], [x, -y, z]])
if not points:
raise ValueError("No intersection points found")
points = np.array(points)
# Sort points using cylindrical coordinates (θ based on x-z plane projection)
theta = np.arctan2(points[:, 0], points[:, 2]) # Angle in x-z plane
sorted_indices = np.lexsort((theta, points[:, 1], points[:, 2]))
sorted_points = points[sorted_indices]
# Spline interpolation
tck, u = splprep(sorted_points.T, s=0.1, per=True) # Periodic if closed curve
u_new = np.linspace(0, 1, 1000)
x_new, y_new, z_new = splev(u_new, tck)
# 3D Plot
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
ax.plot(x_new, y_new, z_new, 'r-', lw=2, label='Elliptic Curve Intersection')
# Sphere visualization (optional wireframe)
theta, phi = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j]
x_sphere = np.sin(phi) * np.cos(theta)
y_sphere = np.sin(phi) * np.sin(theta)
z_sphere = np.cos(phi)
ax.plot_wireframe(x_sphere, y_sphere, z_sphere, color='gray', alpha=0.1)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Smooth Elliptic Curve-Sphere Intersection in Projective Space', pad=15)
ax.legend()
plt.tight_layout()
plt.show()再问是server busy。我等一下再问。