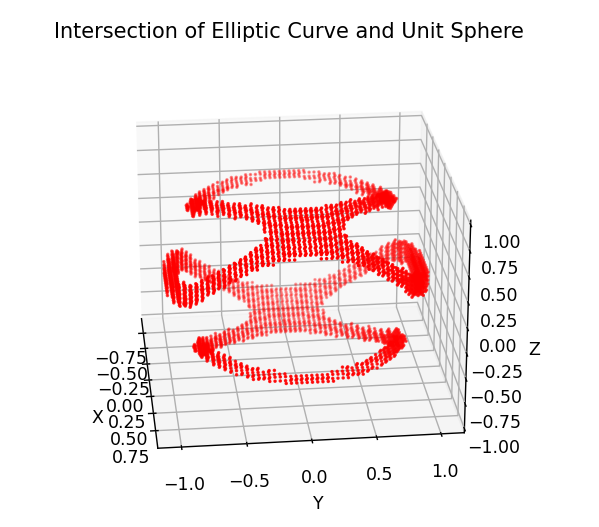
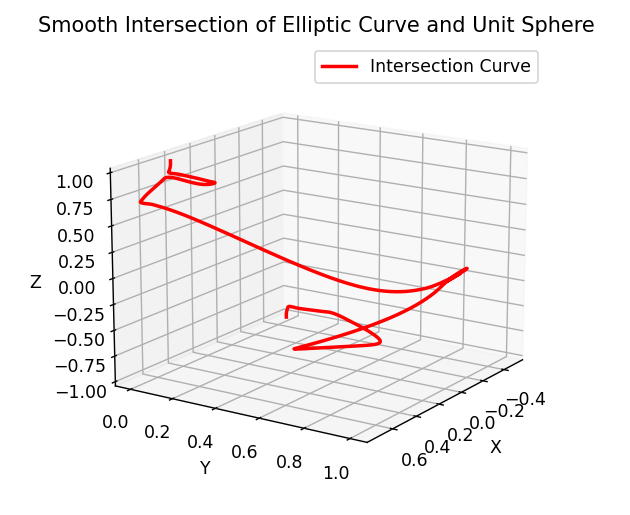
final prompt:
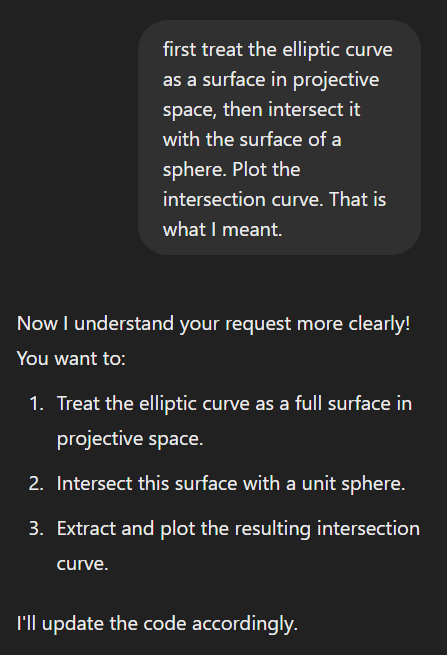
generated code:
代码: 全选
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def elliptic_curve_surface(a, b, res=100):
"""
Generates points on the elliptic curve surface Y^2Z = X^3 + aXZ^2 + bZ^3 in projective space.
"""
X, Z = np.meshgrid(np.linspace(-2, 2, res), np.linspace(-2, 2, res))
Y2 = X**3 + a * X * Z**2 + b * Z**3
real_mask = Y2 >= 0 # Only keep real solutions
Y = np.zeros_like(Y2)
Y[real_mask] = np.sqrt(Y2[real_mask])
return X, Y, Z
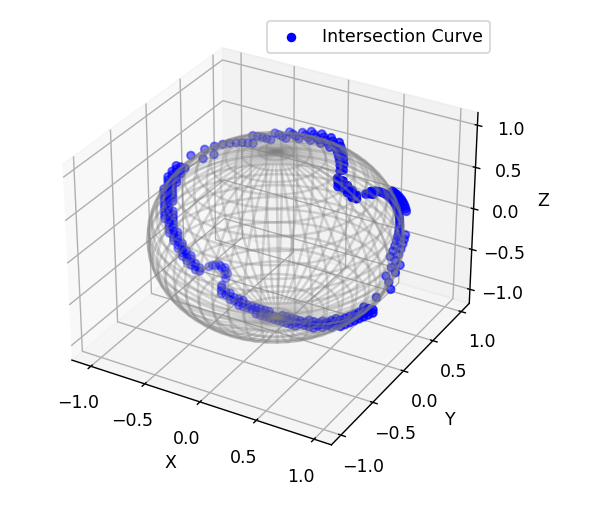
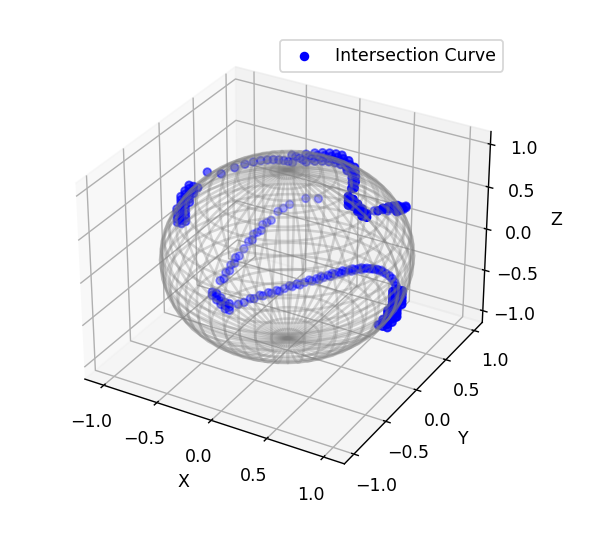
def intersect_with_sphere(X, Y, Z):
"""
Finds the intersection points of the elliptic curve surface with the unit sphere.
"""
norm = np.sqrt(X**2 + Y**2 + Z**2)
mask = np.abs(norm - 1) < 0.05 # Approximate intersection within a small threshold
return X[mask], Y[mask], Z[mask]
def plot_elliptic_curve_intersection(a, b):
"""
Plots the intersection of the elliptic curve surface with the unit sphere.
"""
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Generate elliptic curve surface and intersect with sphere
X, Y, Z = elliptic_curve_surface(a, b)
Xs, Ys, Zs = intersect_with_sphere(X, Y, Z)
# Plot unit sphere
u, v = np.mgrid[0:2*np.pi:50j, 0:np.pi:25j]
sphere_x = np.cos(u) * np.sin(v)
sphere_y = np.sin(u) * np.sin(v)
sphere_z = np.cos(v)
ax.plot_wireframe(sphere_x, sphere_y, sphere_z, color='gray', alpha=0.3)
# Plot intersection curve
ax.scatter(Xs, Ys, Zs, color='b', label='Intersection Curve')
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
ax.legend()
plt.show()
# Example parameters for the elliptic curve
a, b = -2, 1
plot_elliptic_curve_intersection(a, b)