zeta(1/2)的几种算法

[TheMatrix]

natural boundary

嗯。查了一下。以前不知道natural boundary这个名词。

[TheMatrix]

记错了，我还以为是同样的例子。
一本很老的（1950）数学物理教材（Jeffreys)上举过不同的例子。

这个边界上的点，应该都是essential singularity吧？还是说这里不存在这个概念了？可以考虑沿不同曲线趋近于一个边界上的点，比如1，是否得到不同的limit。

嗯。。。不对。你这个例子好像已经说了边界上的点都是有极限的。但是还是认为是singularity，因为从外面不能趋近。也许这种情况下，essential singularity这个概念就不能用了。

感觉对singularity 进行分类都是那种isolated singularity。

或者像整个复平面一样，对无穷远做one point compactification得到黎曼球。这个例子对boundary做one point compactification也得到黎曼球，那么这个boundary就变成一个点，isolated singularity。这样的话，可能确实是essential singularity。

[randomatrices]

前面几个例子，边界上的点应该都是essential singularity，但是好像没有很好的argument去简易地证明，以简单的1为例， 从内趋近，极限lim_{z->1-}(z-1)^n(z+z^2+z^4+z^8+z^16+z^32+ ...)对于任意n都不存在？

这个边界上的点，应该都是essential singularity吧？还是说这里不存在这个概念了？可以考虑沿不同曲线趋近于一个边界上的点，比如1，是否得到不同的limit。

嗯。。。不对。你这个例子好像已经说了边界上的点都是有极限的。但是还是认为是singularity，因为从外面不能趋近。也许这种情况下，essential singularity这个概念就不能用了。

感觉对singularity 进行分类都是那种isolated singularity。

或者像整个复平面一样，对无穷远做one point compactification得到黎曼球。这个例子对boundary做one point compactification也得到黎曼球，那么这个boundary就变成一个点，isolated singularity。这样的话，可能确实是essential singularity。

[TheMatrix]

2，

这个2，我查了一下Russian Wiki，有这个叙述（翻译过来之后）：

[changbaihou]

这个2，我查了一下Russian Wiki，有这个叙述（翻译过来之后）：

这几个是同样的approach，区别就在于在用了几步integration by parts后停下来而己。比如，比(3)再多走一步，就能得到

zeta(1/2)=\sum_{n\leg N}n^{-1/2}-2\sqrt{N}-1/{2\sqrt{N}}+N^{-3/2}/24-(1/2)*(3/2)*(5/2)N^{-7/2}+R

这里R等于

(1/2)*(3/2)*(5/2)*(7/2)*(9/2)*(11/2)*(1/1440)*\int_N^{\infty}({x}-{x}^2)^2*(1+2{x}-2{x}^2)*x^{-13/2}dx.

{x}=x-[x]是x的fractional part。用最粗糙的估计能得到，0<R=\leq (1/2)*(3/2)*(5/2)*(7/2)*(9/2)*(1/1440)*(1/16)N^{-11/2}。如果像前文提到有人能取N=10000，那么这儿有0<R<1.29x10^{-25}。所以(as long as you can calculate \sum_{n\leq 10000}n^{-1/2})很容易精确到小数点后25位。如果你只有一个小计算器，只方便"手"算前10位的1/sqrt{n}的和，要想精确到前10来位(小计算器精度)，其实也只需要比上述估计多算一项就够了。

[TheMatrix]

这几个是同样的approach，区别就在于在用了几步integration by parts后停下来而己。比如，比(3)再多走一步，就能得到

zeta(1/2)=\sum_{n\leg N}n^{-1/2}-2\sqrt{N}-1/{2\sqrt{N}}+N^{-3/2}/24-(1/2)*(3/2)*(5/2)N^{-7/2}+R

这里R等于

(1/2)*(3/2)*(5/2)*(7/2)*(9/2)*(11/2)*(1/1440)*\int_N^{\infty}({x}-{x}^2)^2*(1+2{x}-2{x}^2)*x^{-13/2}dx.

{x}=x-[x]是x的fractional part。用最粗糙的估计能得到，0<R=\leq (1/2)*(3/2)*(5/2)*(7/2)*(9/2)*(1/1440)*(1/16)N^{-11/2}。如果像前文提到有人能取N=10000，那么这儿有0<R<1.29x10^{-25}。所以(as long as you can calculate \sum_{n\leq 10000}n^{-1/2})很容易精确到小数点后25位。如果你只有一个小计算器，只方便"手"算前10位的1/sqrt{n}的和，要想精确到前10来位(小计算器精度)，其实也只需要比上叙估计多算一项就够了。

哦。Russian Wiki那里的展开式你推出来了。我没推出来。你说的integration by parts是积分哪个函数？

[randomatrices]

Euler-Maclaurin Approximation

哦。Russian Wiki那里的展开式你推出来了。我没推出来。你说的integration by parts是积分哪个函数？

[TheMatrix]

Euler-Maclaurin Approximation

我试过这个，好像对不上啊：



好像没有用到分部积分法。

[randomatrices]

有一种推导euler-maclaurin formula就是不断做分部积分，
下面这个人讲的很清楚

我试过这个，好像对不上啊：



好像没有用到分部积分法。

[randomatrices]

明白了， 那个approximation是基于s>1的情况做出的， 然后analytic continuation 到s<1的case.
如果你一开始就从s=1/2是推不出来的， 因为有的积分会 blow up.

我试过这个，好像对不上啊：



好像没有用到分部积分法。

[randomatrices]

欧拉为解决Basel问题，只算了初始9项加9项伯努利系数相关近似项， 得到十七位精度。如果用蛮力去加一项项初始项， 即使加到十万亿项也只能得到十位精度。
9项近似项也几乎是最佳值， 因为更多的近似项并不能带来明显更高的精度， 而且在六十项近似项后更多的近似项会让精度急剧降低。

问题来了， 对一般的函数， 如果做Euler–Maclaurin 近似，怎么决定较佳的近似项数？

[TheMatrix]

欧拉为解决Basel问题，只算了初始9项加9项伯努利系数相关近似项， 得到十七位精度。如果用蛮力去加一项项初始项， 即使加到十万亿项也只能得到十位精度。
9项近似项也几乎是最佳值， 因为更多的近似项并不能带来明显更高的精度， 而且在六十项近似项后更多的近似项会让精度急剧降低。

问题来了， 对一般的函数， 如果做Euler–Maclaurin 近似，怎么决定较佳的近似项数？

看了那个视频。确实不错。

看到了最后对error term的评论，确实令人惊讶，error term还会越来越大。

[changbaihou]

有一种推导euler-maclaurin formula就是不断做分部积分，
下面这个人讲的很清楚

That's exactly what I was talking about. Applying the Euler-MacLaurin Summation (up to a certain order of derivatives) is the same as repeatedly applying the method of integration by parts.

Suppose f(x) is sufficiently smooth. Then by Stieltjes integration,

\sum_{a<n\leq b}f(x)=\int_{a}^{b}f(x)d[x]=\int_{a}^{b}f(x)dx - \int_{a}^{b}f(x)db_1(x) ....(*)

where [x] is the integer part of x, b_1(x)={x}-1/2 (with {x}=x-[x] being the fractional part of x). Let
b_2(x)= {x}^2/2-{x}/2+1/12,
b_3(x)={x}^3/6-{x}^2/4+{x}/12,
b_4(x)={x}^4/24-{x}^3/12+{x}^2/24-1/720,
.....
All b_j(x) are period 1 functions satisfying [b_{j+1}(x)]'=b_j(x), and \int_0^1{b_j(x)}dx=0

Now, (repeatedly) applying integration by parts to the last integral in (*), we get

\sum_{a<n\leq b}f(x)=\int_{a}^{b}f(x)dx - f(x)*b_1(x)|_{a}^{b}+\int_{a}^{b}f'(x)db_2(x)=....
=\int_{a}^{b}f(x)dx+\sum_{j=1}^{l}(-1)^jb_j(x)f^(j-1)(x)|_{a}^{b}+(-1)^{l+1}\int_{a}^{b}b_l(x)f^(l)(x)dx (**)

which is the general Euler-MacLaurin Summation formula.

When Re(s)>1, we have
\zeta(s)=\sum_{n\leq N}n^{-s}+\lim_{b\to \infty} \sum_{N<n\leq b}n^{-s} (***)

Applying the Euler-MacLaurin summation (**) to the last sum in (***), we get an analytic extension of \zeta(s) to Re(s)>1-l with which we can directly calculate \zeta(1/2).

(I should mention that one can easily show that \zeta(-2n)=0 directly from using the Euler-MacLaurin summation formula to \sum_{n=1}^{\infty}n^{-s}, though it requires some extra effort if you want to show that s=-2n is a SIMPLE zero.)

[TheMatrix]

明白了， 那个approximation是基于s>1的情况做出的， 然后analytic continuation 到s<1的case.
如果你一开始就从s=1/2是推不出来的， 因为有的积分会 blow up.

嗯。这个地方要从Re(s)>1推，然后还是用到解析延拓。很好。

你那个视频对Euler-Maclaurin公式的推导讲得很好。下面这个是结果：



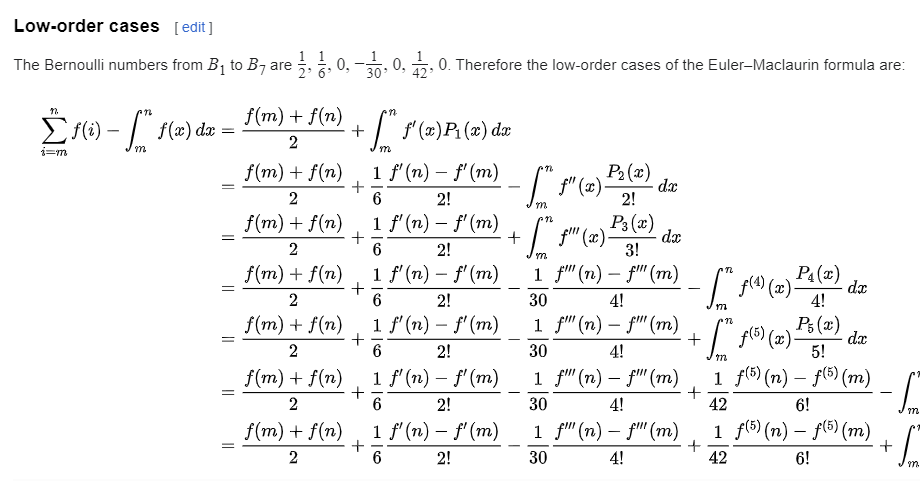
我从这个结果出发，试图推Russian Wiki上的展开式：



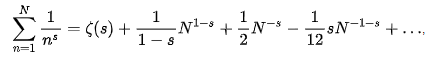
我用的是从m=1 到 n=N，展开式中N的幂次项都对上了，对应Euler-Maclaurin公式中的f(n),f'(n),f'''(n)等。但是m=1的那些项，f(m),f'(m),f'''(m)，加起来应该得到zeta(s)的，我还没有得出来，得到的是：
1/(s-1)+1/2+s*B₂/2!+s(s+1)(s+2)*B₄/4!+...

[TheMatrix]

That's exactly what I was talking about. Applying the Euler-MacLaurin Summation (up to a certain order of derivatives) is the same as repeatedly applying the method of integration by parts.

Suppose f(x) is sufficiently smooth. Then by Stieltjes integration,

\sum_{a<n\leq b}f(x)=\int_{a}^{b}f(x)d[x]=\int_{a}^{b}f(x)dx - \int_{a}^{b}f(x)db_1(x) ....(*)

where [x] is the integer part of x, b_1(x)={x}-1/2 (with {x}=x-[x] being the fractional part of x). Let
b_2(x)= {x}^2/2-{x}/2+1/12,
b_3(x)={x}^3/6-{x}^2/4+{x}/12,
b_4(x)={x}^4/24-{x}^3/12+{x}^2/24-1/720,
.....
All b_j(x) are period 1 functions satisfying [b_{j+1}(x)]'=b_j(x), and \int_0^1{b_j(x)}dx=0

Now, (repeatedly) applying integration by parts to the last integral in (*), we get

\sum_{a<n\leq b}f(x)=\int_{a}^{b}f(x)dx - f(x)*b_1(x)|_{a}^{b}+\int_{a}^{b}f'(x)db_2(x)=....
=\int_{a}^{b}f(x)dx+\sum_{j=1}^{l}(-1)^jb_j(x)f^(j-1)(x)|_{a}^{b}+(-1)^{l+1}\int_{a}^{b}b_l(x)f^(l)(x)dx (**)

which is the general Euler-MacLaurin Summation formula.

When Re(s)>1, we have
\zeta(s)=\sum_{n\leq N}n^{-s}+\lim_{b\to \infty} \sum_{N<n\leq b}n^{-s} (***)

Applying the Euler-MacLaurin summation (**) to the last sum in (***), we get an analytic extension of \zeta(s) to Re(s)>1-l with which we can directly calculate \zeta(1/2).

(I should mention that one can easily show that \zeta(-2n)=0 directly from using the Euler-MacLaurin summation formula to \sum_{n=1}^{\infty}n^{-s}, though it requires some extra effort if you want to show that s=-2n is a SIMPLE zero.)

你这个是推Euler-Maclaurin公式吧？那个视频我看了，very accessible。

[changbaihou]

你这个是推Euler-Maclaurin公式吧？那个视频我看了，very accessible。

是。因为随机矩阵说Euler-MacLaurin和分步积分关系，所以我说That's exactly what I was talking about，然后随手写了推导。很抱歉如果跟视频里重复了。

[TheMatrix]

是。因为随机矩阵说Euler-MacLaurin和分步积分关系，所以我说That's exactly what I was talking about，然后随手写了推导。很抱歉如果跟视频里重复了。

这个推导还是很技术化的，没有视频带着很难跟下去。

[randomatrices]

又清楚了一点，SIMPLE zero那儿我还得再想想。

That's exactly what I was talking about. Applying the Euler-MacLaurin Summation (up to a certain order of derivatives) is the same as repeatedly applying the method of integration by parts.

Suppose f(x) is sufficiently smooth. Then by Stieltjes integration,

\sum_{a<n\leq b}f(x)=\int_{a}^{b}f(x)d[x]=\int_{a}^{b}f(x)dx - \int_{a}^{b}f(x)db_1(x) ....(*)

where [x] is the integer part of x, b_1(x)={x}-1/2 (with {x}=x-[x] being the fractional part of x). Let
b_2(x)= {x}^2/2-{x}/2+1/12,
b_3(x)={x}^3/6-{x}^2/4+{x}/12,
b_4(x)={x}^4/24-{x}^3/12+{x}^2/24-1/720,
.....
All b_j(x) are period 1 functions satisfying [b_{j+1}(x)]'=b_j(x), and \int_0^1{b_j(x)}dx=0

Now, (repeatedly) applying integration by parts to the last integral in (*), we get

\sum_{a<n\leq b}f(x)=\int_{a}^{b}f(x)dx - f(x)*b_1(x)|_{a}^{b}+\int_{a}^{b}f'(x)db_2(x)=....
=\int_{a}^{b}f(x)dx+\sum_{j=1}^{l}(-1)^jb_j(x)f^(j-1)(x)|_{a}^{b}+(-1)^{l+1}\int_{a}^{b}b_l(x)f^(l)(x)dx (**)

which is the general Euler-MacLaurin Summation formula.

When Re(s)>1, we have
\zeta(s)=\sum_{n\leq N}n^{-s}+\lim_{b\to \infty} \sum_{N<n\leq b}n^{-s} (***)

Applying the Euler-MacLaurin summation (**) to the last sum in (***), we get an analytic extension of \zeta(s) to Re(s)>1-l with which we can directly calculate \zeta(1/2).

(I should mention that one can easily show that \zeta(-2n)=0 directly from using the Euler-MacLaurin summation formula to \sum_{n=1}^{\infty}n^{-s}, though it requires some extra effort if you want to show that s=-2n is a SIMPLE zero.)

[randomatrices]

这儿Euler-Maclaurin近似用在N to infinity, 从1到N，add literally, 然后再让N趋向无穷.
changbaihou回我的那个帖子也讲到了， 如果你仔细看看就会找到。
remainder terms 决定了你能解析延拓s到哪里和s不能取哪些值， 这是我的理解。

嗯。这个地方要从Re(s)>1推，然后还是用到解析延拓。很好。

你那个视频对Euler-Maclaurin公式的推导讲得很好。下面这个是结果：



我从这个结果出发，试图推Russian Wiki上的展开式：



我用的是从m=1 到 n=N，展开式中N的幂次项都对上了，对应Euler-Maclaurin公式中的f(n),f'(n),f'''(n)等。但是m=1的那些项，f(m),f'(m),f'''(m)，加起来应该得到zeta(s)的，我还没有得出来，得到的是：
1/(s-1)+1/2+s*B₂/2!+s(s+1)(s+2)*B₄/4!+...

[TheMatrix]

这儿Euler-Maclaurin近似用在N to infinity, 从1到N，add literally, 然后再让N趋向无穷.
changbaihou回我的那个帖子也讲到了， 如果你仔细看看就会找到。
remainder terms 决定了你能解析延拓s到哪里和s不能取哪些值， 这是我的理解。

哦。知道了。我把Euler-Maclaurin用在从1到N了。反过来一看就容易了。谢谢！