好像不对吧。试一下
a=b=1
y=2
x=-2
z=2
版主: verdelite, TheMatrix

噢,我算错了。这个画直线得交点的方法,除了椭圆曲线之外,还可以用于求所有的勾股数x^2+y^2=z^2。此法还可以用于什么问题?TheMatrix 写了: 2023年 1月 27日 18:05 我得到的是:
x=((2m^2+1)x_0 - (4m) y_0)/(2m^2-1)
y=(x+x_0)/(2m) -y_0
y_0前面有个系数(4m)。


哦对。是我糊涂了。我在想的是x2+1=2y2。yilou 写了: 2023年 1月 28日 12:11 显然这是平方差为0的情形。要想排除0的情形只需要a≠b。
这个通解两百年前Gauss就有了。三姐夫说这个是Gauss integer quadratic ring UFD Z[ i ]里的elementary result, 还说了一堆class number one之类的。
我一个文科生不是很懂,但是ctrl-c/ctrl-p还是驾轻就熟的

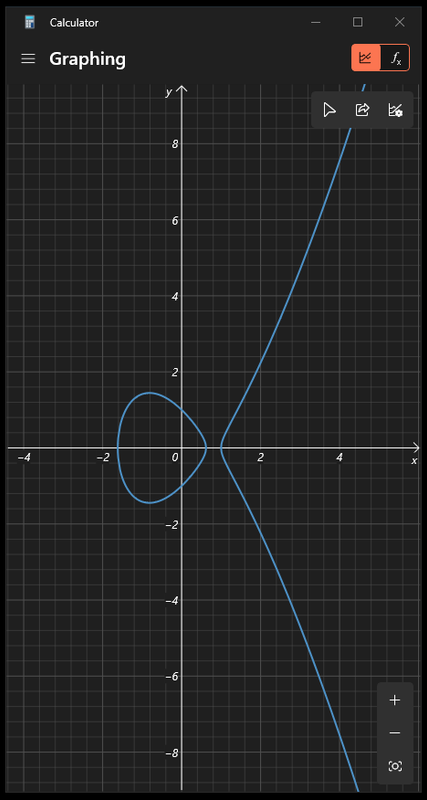
Windows 10计算机能画图了。画的还不错。这个是y2=x3-2x+1的图。TheMatrix 写了: 2023年 1月 28日 13:10 哦对。是我糊涂了。我在想的是x2+1=2y2。
你这个展开就是:
x,z= a2±2ab-b2
y=a2+b2
是。这个问题是Pell方程,有好几种解法:
1,连分数:https://mathworld.wolfram.com/PellEquation.html
2,考虑x2+1=2y2。x=(An+Bn)/2, y=(An-Bn)/(2√2) where A,B = 1±√2, n be odd. Also see https://mathworld.wolfram.com/PellEquation.html
3,Gauss integer - 就是你这里的解法。
4,与有理直线的交点 - 参考椭圆曲线交点的方法。
(ヅ) 写了: 2023年 1月 27日 12:05 也在想这个问题,猜测可能是无穷多
上面就有3组
x = 2, y = 58, z = 82, diff = 3360
x = 46, y = 74, z = 94, diff = 3360
x = 97, y = 113, z = 127, diff = 3360
x = 62, y = 218, z = 302, diff = 43680
x = 103, y = 233, z = 313, diff = 43680
x = 334, y = 394, z = 446, diff = 43680
x = 146, y = 386, z = 526, diff = 127680
x = 503, y = 617, z = 713, diff = 127680
x = 718, y = 802, z = 878, diff = 127680
总结的不错!TheMatrix 写了: 2023年 1月 28日 13:10 哦对。是我糊涂了。我在想的是x2+1=2y2。
你这个展开就是:
x,z= a2±2ab-b2
y=a2+b2
是。这个问题是Pell方程,有好几种解法:
1,连分数:https://mathworld.wolfram.com/PellEquation.html
2,考虑x2+1=2y2。x=(An+Bn)/2, y=(An-Bn)/(2√2) where A,B = 1±√2, n be odd. Also see https://mathworld.wolfram.com/PellEquation.html
3,Gauss integer - 就是你这里的解法。
4,与有理直线的交点 - 参考椭圆曲线交点的方法。
才发现题都没读全就在开黄腔了,汗。verdelite 写了: 2023年 1月 27日 10:44 大史老师布置了一个习题:写出三个不同的平方数,他们之间有等差关系。就是说,z^2-y^2=y^2-x^2。不许相互讨论通气。
结果三个好朋友学生交上作业后,老师给了0分。学生很委屈,说,我们三人给的答案各不相同,怎么能说我们讨论通气呢?老师说,你们看看,你们是好朋友,还有,你们的答案虽然各不相同,但是你们的答案里,那差值却是一样的。
后来证实,这三个人被三体人发展为ETO组织成员。他们做作业的方法就是问三体人给他们提供的chatGPT接口。chatGPT先是给了三个一样的答案,结果他们说不行。chatGPT就给了他们这交上来的三个不同答案,但是可能理解题意偏差,给的三个答案却享用同一个差值。这是一个科幻小说里面的一个情节。
放开小说不说,那么你知道他们的答案是什么吗?
(原先写成ECO,现在改了)
如果原来的条件换成"等差数列a, b, c满足abc为平方数,而且要求相同公差有两组以上答案",貌似简单了很多,其实难度是差不多的。当然通过计算机找例子会容易得多。san721 写了: 2023年 2月 12日 00:19 才发现题都没读全就在开黄腔了,汗。
如果K>0是公差,原题相当于椭圆曲线E_K: y^2=x^3-K^2x上有三个以上的整点,而且每点都是E_K上某一非torsion有理点的2倍。现在的问题是问是否存在无穷多的这种K。我猜测答案是Yes,但证明应该是无望的。这是非常难的一道题。

怎么会出现立方?san721 写了: 2023年 2月 12日 00:19 才发现题都没读全就在开黄腔了,汗。
如果K>0是公差,原题相当于椭圆曲线E_K: y^2=x^3-K^2x上有三个以上的整点,而且每点都是E_K上某一非torsion有理点的2倍。现在的问题是问是否存在无穷多的这种K。我猜测答案是Yes,但证明应该是无望的。这是非常难的一道题。
y^2=x^3-K^2x=(x-K)x(x+K)。对于这种有full 2-torsion的椭圆曲线,(x, y)是一有理点的2倍if and only if x-K, x及x+K都是有理数的平方。x是整数的话,正好x-K, x及x+K都是整数平方。
san721 写了: 2023年 2月 12日 00:19 才发现题都没读全就在开黄腔了,汗。
如果K>0是公差,原题相当于椭圆曲线E_K: y^2=x^3-K^2x上有三个以上的整点,而且每点都是E_K上某一非torsion有理点的2倍。现在的问题是问是否存在无穷多的这种(square-free的)K。我猜测答案是Yes,但证明应该是无望的。这是非常难的一道题。

没明白为什么x-K, x及x+K三个数要相乘。san721 写了: 2023年 2月 13日 22:14 y^2=x^3-K^2x=(x-K)x(x+K)。对于这种有full 2-torsion的椭圆曲线,(x, y)是一有理点的2倍if and only if x-K, x及x+K都是有理数的平方。x是整数的话,正好x-K, x及x+K都是整数平方。
我收回我第一个贴子了。这些E_K都是某一条曲线的二次扭曲线(quadratic twists)。对于generic的一条椭圆曲线,证明其有无穷多的二次扭曲线包含起码三个整点应该是非常难的。但对于某些特殊曲线,可能能构造出满足条件的quadratic twists。我其实是刚看到了kde23的贴子才醒悟过来,lol。TheMatrix 写了: 2023年 2月 13日 22:35 没明白为什么x-K, x及x+K三个数要相乘。
不过原题中说三个人给出的答案中的差值是相同的。这个要求在前面的回答中都没用上。你是要满足这个要求吗?

我回去看了一下kde123的贴,才明白原题中三个人都找到的等差三元组(x2,y2,z2)的三个公差是一样的。这个要求不容易表达,尤其是用自然语言。当时我看到了,看了一遍没看懂,当成故事情节了。加了这个要求确实要难一些了。san721 写了: 2023年 2月 13日 23:29 我收回我第一个贴子了。这些E_K都是某一条曲线的二次扭曲线(quadratic twists)。对于generic的一条椭圆曲线,证明其有无穷多的二次扭曲线包含起码三个整点应该是非常难的。但对于某些特殊曲线,可能能构造出满足条件的quadratic twists。我其实是刚看到了kde23的贴子才醒悟过来,lol。
原题不是要求成等差的三个平方数吗?如果椭圆曲线是y^2=x(x-a)(x-b)的形式,而且P是其上面的一有理点,那么2P的坐标(x,y)满足x,x-a,x-b都为有理数平方。所以如果(x,y)是E_K: y^2=x^3-K^2x=x(x-K)(x+K)上一整点,而且是某一有理点的2倍,那x, x-K,x+K不都是有理数(从而整数)平方了吗?所有就有公差为K的三平方数了。对于一般的一条椭圆曲线,构造无穷多的quadratic twists使其每条都包含起码一无穷阶的整点是很容易的(尽管不能保证其为某有理点2倍),但要确保有两个以上整点就很难了。

用有理点的方法可以得到上一步。kde23 写了: 2023年 1月 28日 18:39 试给个"通解",结论如下:
对任意两个整数u,v, 令
x = x(u,v) = u^2 + 2uv - v^2
y = y(u,v) = u^2 + v^2
z = z(u,v) = u^2 - 2uv - v^2
则可验证 x^2-y^2 = y^2-z^2
记 f(u,v) = x^2 - y^2 = (u^2 + 2uv - v^2)^2 - (u^2 + v^2)^2
则也有 f(u,v) = y^2 - z^2
kde23 写了: 2023年 1月 28日 18:39
设m为任意整数,令
p = m^2+m+1
q = 2m+1
r = m^2-1
则经过计算,可知
f(p,q) = f(p, r) = f(q+r, p)

哦,你得到的这个表达式比较简单:kde23 写了: 2023年 1月 28日 18:39 试给个"通解",结论如下:
对任意两个整数u,v, 令
x = x(u,v) = u^2 + 2uv - v^2
y = y(u,v) = u^2 + v^2
z = z(u,v) = u^2 - 2uv - v^2
则可验证 x^2-y^2 = y^2-z^2
记 f(u,v) = x^2 - y^2 = (u^2 + 2uv - v^2)^2 - (u^2 + v^2)^2
则也有 f(u,v) = y^2 - z^2

这个表达式是比较简单。可以写成,设这个差为K,那么