FoxMe 写了: 2023年 10月 15日 17:43
1,两个曲线E1和E2,如果isogenous的话。torsion point一定映射到torsion point上。对吧?那么对应点order是相同的吗?两个曲线rank也相同吗?
isogeny是群同态,如果a是整数,那么phi(ax)=a phi(x),所以它们的order相同。isogeny是(有限)多对一,对Z-模rank没有影响,所以rank也相同。
2,假如两个曲线,rank不相同,它们之间能有isogeny吗?
应该不能。
3,两个曲线,有isogeny的话,一定有isomorphism吗?
两条曲线之间的isogeny构成一个加法群,不见得有isomorphism.
我现在有一个推理把我绕糊涂了。我说一下你看看:
假如只考虑同一个椭圆曲线E/Q。根据Mordell定理,它是finitely generated。所以torsion points,也是torsion subgroup,为有限。
现在考虑乘以2这个isogeny,这是自映射,表示为[2]。也就是[2](x)=2x=x+x。
在这个映射下,torsion points一定映射到torsion points。非torsion points一定映射到非torsion points。
也就是在[2]这个自映射下,torsion subgroup映射到自己,而且是一个满射,这是因为:
1,非torsion points不能映射到torsion points。
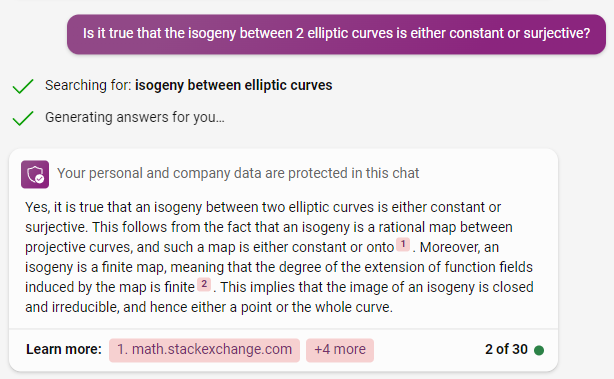
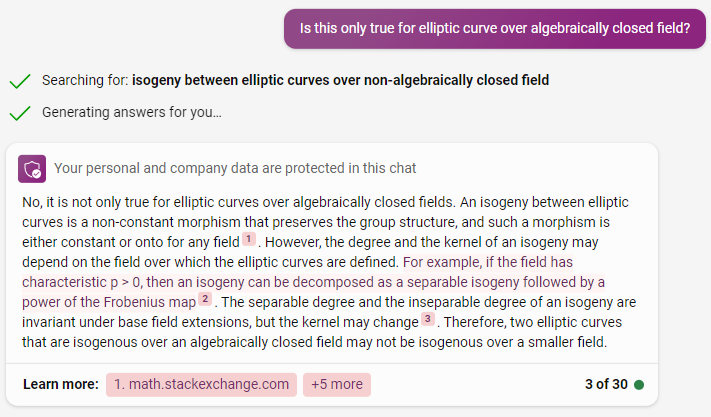
2,整个这个映射 [2]: E --> E 是满射 - 因为一个isogeny,如果不是全部映射到0点的话,那么一定是满射 - 这是一个定理。
也就是说,[2]这个自映射,从torsion subgroup来看,是满射,所以kernel为0,所以也是单射。
所以整个这个 [2]: E --> E,也是单射 - 因为kernel为0。前面说了,它又是一个满射。所以这是一个一一映射。
所以[2]是一个automorphism啊。这个推理有问题吗?