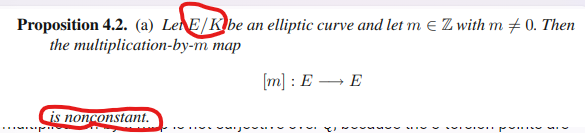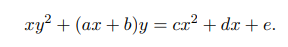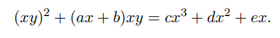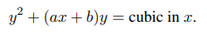分页: 8 / 9
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 19日 11:10
由 FoxMe
好,若n不为零,[n]: E1(\bar{K})->E2(\bar{K})是满射。现在的问题是:
如果K不是代数封闭的,那么isogeny也是0或满射吗?
其实这个问题归结为:如果K不是代数封闭的,那么morphism也是0或满射吗?
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 19日 21:07
由 TheMatrix
FoxMe 写了: 2023年 10月 19日 11:10
好,若n不为零,[n]: E1(\bar{K})->E2(\bar{K})是满射。现在的问题是:
如果K不是代数封闭的,那么isogeny也是0或满射吗?
其实这个问题归结为:如果K不是代数封闭的,那么morphism也是0或满射吗?
对。是这个问题。
Silverman那本书的convention,不提K的话,就是指代数闭包。但是他没提K的情况,也就是不是代数闭包的情况。
Bing Chat是说不需要代数封闭域的。
viewtopic.php?p=2169096#p2169096
changbaihou应该是对的。我又修正了几遍Bing chat的prompt。它是这么回答的:
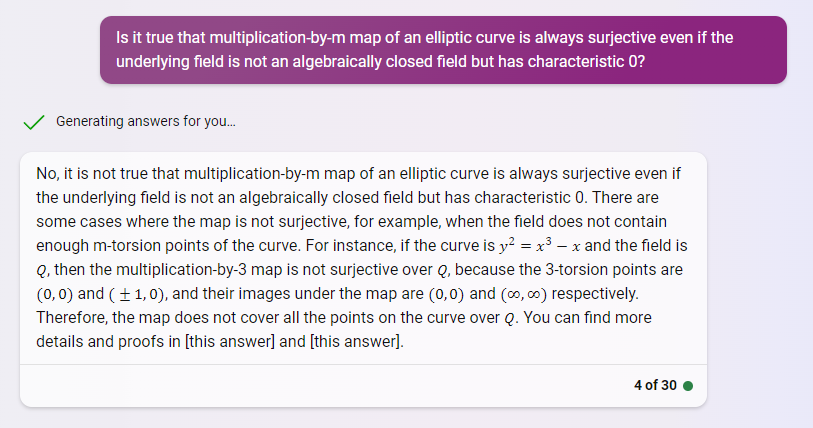
但是它不会是[0]:
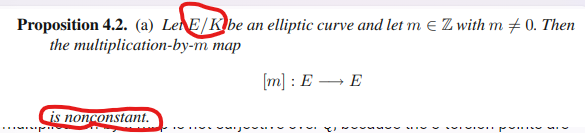
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 19日 21:55
由 TheMatrix
TheMatrix 写了: 2023年 10月 19日 21:07
对。是这个问题。
Silverman那本书的convention,不提K的话,就是指代数闭包。但是他没提K的情况,也就是不是代数闭包的情况。
Bing Chat是说不需要代数封闭域的。
viewtopic.php?p=2169096#p2169096
changbaihou应该是对的。我又修正了几遍Bing chat的prompt。它是这么回答的:

但是它不会是[0]:
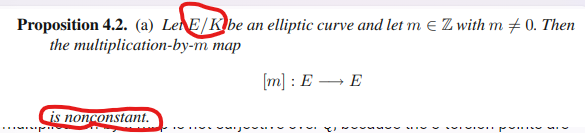
来看看这个定理。有没有说K是不是algebraically closed?
从它下面提到\bar{K}来看,应该不是。而且这本书的convention是,如果不提K,那就是underlying field就是algebraically closed,如果显式提到K,比如E/K,那就是不要求algebraically closed,因为会提到\bar{K}/K。
所以从定理的叙述看,K不需要是algebraically closed。但是它的证明似乎又用到algebraically closed的性质。比如画红线的地方,二阶torsion points只能有有限个,所以隐含说一定有不是2阶的。他是不是隐含说曲线上有无穷多个点?后面证明奇数倍乘不为[0]的时候,用到\bar{K}了,然后它又没有降回K。

Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 21日 08:39
由 changbaihou
FoxMe 写了: 2023年 10月 19日 11:10
好,若n不为零,[n]: E1(\bar{K})->E2(\bar{K})是满射。现在的问题是:
如果K不是代数封闭的,那么isogeny也是0或满射吗?
其实这个问题归结为:如果K不是代数封闭的,那么morphism也是0或满射吗?
Isogeny所提到的满射和K没太多关系,因为只是在说它在K的代数闭包上是满射。当然K是代数闭的时候在K上就是满射,不是代数闭的时候很可能就不是满射(除了multiply by 1,by -1这些)。当然answer to your last question也是No了。
把在\bar{K}上isogeny是满射放在其定义里可以有,但如果用isogeny的具体形式(image 的components都K-rational functions的一个morphism)代替可能更直观。对了,大家说isogeny时一般都自动assume它不是0映射,有人把[0]当做一个isogeny只是为了方便描述isogeny集合的代数结构。就象矩阵里eigenvectors都不为0,但把0向量加进去就有了eigen-SPACE一样。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 21日 10:43
由 TheMatrix
changbaihou 写了: 2023年 10月 21日 08:39
Isogeny所提到的满射和K没太多关系,因为只是在说它在K的代数闭包上是满射。当然K是代数闭的时候在K上就是满射,不是代数闭的时候很可能就不是满射(除了multiply by 1,by -1这些)。当然answer to your last question也是No了。
嗯。对。Silverman书里在\bar{K}和K之间跳来跳去,把我弄糊涂了。
所以,一个number field,根据Mordell定理,椭圆曲线是finitely generated。所以torsion subgroup为有限。
这句话还是对的:[m]映射把torsion points映射成torsion points,把非torsion points映射成非torsion points。
而torsion points为有限,当m为torsion subgroup的阶的时候,[m]把所有的torsion points都映射为0。而这些torsion points本身不能被映射到,所以这个[m]不是满射。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 21日 11:40
由 changbaihou
TheMatrix 写了: 2023年 10月 21日 10:43
嗯。对。Silverman书里在\bar{K}和K之间跳来跳去,把我弄糊涂了。
所以,一个number field,根据Mordell定理,椭圆曲线是finitely generated。所以torsion subgroup为有限。
这句话还是对的:[m]映射把torsion points映射成torsion points,把非torsion points映射成非torsion points。
而torsion points为有限,当m为torsion subgroup的阶的时候,[m]把所有的torsion points都映射为0。而这些torsion points本身不能被映射到,所以这个[m]不是满射。
对,K是个代数数域的话,E(K)的torsion part和rank都是有限的。如果|m|>1,那[m]: E(K)->E(K)是满射if and only if rank(E(K))=0,而且m和|E(K)|互素。所以只要rank(E(K))=0,还是有infinitely many m使得[m]: E(K)->E(K)是满射的。比如K=Q,如果rank(E(Q))=0,那么对任何素数p>7,[p]: E(Q)->E(Q)是满射。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 21日 14:17
由 TheMatrix
changbaihou 写了: 2023年 10月 21日 11:40
对,K是个代数数域的话,E(K)的torsion part和rank都是有限的。如果|m|>1,那[m]: E(K)->E(K)是满射if and only if rank(E(K))=0,而且m和|E(K)|互素。所以只要rank(E(K))=0,还是有infinitely many m使得[m]: E(K)->E(K)是满射的。比如K=Q,如果rank(E(Q))=0,那么对任何素数p>7,[p]: E(Q)->E(Q)是满射。
嗯。这是Mazur定理。我刚看到这里:

这个结论好像也是令人惊讶的 - E(Q)不存在很大的torsion group。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 21日 16:10
由 FoxMe
rank(E(K))>0会出现什么情况?[m]不是满射吗?那么“isogeny非零即满射”这个结论在代数数域上就不成立了。
changbaihou 写了: 2023年 10月 21日 11:40
对,K是个代数数域的话,E(K)的torsion part和rank都是有限的。如果|m|>1,那[m]: E(K)->E(K)是满射if and only if rank(E(K))=0,而且m和|E(K)|互素。所以只要rank(E(K))=0,还是有infinitely many m使得[m]: E(K)->E(K)是满射的。比如K=Q,如果rank(E(Q))=0,那么对任何素数p>7,[p]: E(Q)->E(Q)是满射。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 21日 17:24
由 changbaihou
FoxMe 写了: 2023年 10月 21日 16:10
rank(E(K))>0会出现什么情况?[m]不是满射吗?那么“isogeny非零即满射”这个结论在代数数域上就不成立了。
E(K)是个free abelian group。如果rank>0, E(K)有non-trivial的free part P_1Z+aP_2Z+..., 这里{P_1, P_2,...}是free part的一组generators。只要|m|>1,那P_1就不在m(E(K))里,所以[m]不可能是满射。
先前说过了,[m]: E(\bar(K))->E(\bar(K))才是满射,一般情况下[m]: E(K)->E(K)不是满射。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 21日 17:25
由 FoxMe
有限域上的椭圆曲线是另一种情况:所有的点都是torsion.
TheMatrix 写了: 2023年 10月 21日 14:17
嗯。这是Mazur定理。我刚看到这里:

这个结论好像也是令人惊讶的 - E(Q)不存在很大的torsion group。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 21日 17:29
由 FoxMe
明白了,多谢

。这里容易混淆,书上也不大明确。
changbaihou 写了: 2023年 10月 21日 17:24
E(K)是个free abelian group。如果rank>0, E(K)有non-trivial的free part P_1Z+P_2Z+..., 这里{P_1, P_2,...}是free part的一组generators。只要|m|>1,那P_1就不在m(E(K))时,所以[m]不可能是满射。
先前说过了,[m]: E(\bar(K))->E(\bar(K))才是满射,一般情况下[m]: E(K)->E(K)不是满射。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 22日 15:54
由 TheMatrix
TheMatrix 写了: 2023年 9月 28日 15:12
最后应该怎么弄呢?在UTM那本书里,第17页,比较靠前了,呵呵。但是这页书也不好看:

这页书说的是这个意思:
1,用projective linear的方式,也就是非齐次方程的fractional linear的方式,可以把椭圆曲线最一般形式变成这个形式:
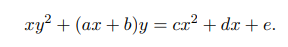
2,然后两边乘以x,变成
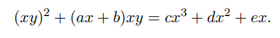
再用换元xy -> y,也可以说是 Y=a
21X'+a
22Y'+a
23Z' with a
22=X',a
21=a
23=0,把它变为
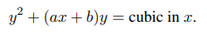
注意这一步不是线性变换。
这一步是神来之笔。但是神来之笔又是怎么来的呢?是人家把椭圆曲线的几何研究清楚了,才有这么一个神来之笔。它的思路也在这一页里,就是第一段,和中间那个图。
3,再做一个简单的线性变换,就变成Weierstrass标准形式了。
4,再做一个线性变换,就变成Weierstrass最简形式了。
用sympy算了一下。
假设椭圆曲线是一个一般三次曲线:
x**3 + 9*x**2*y + 4*x**2 - 5*x*y**2 - 2*x*y - 9*x - 5*y**3 + 7*y**2 + y - 1
齐次化:
X**3 + 9*X**2*Y + 4*X**2*Z - 5*X*Y**2 - 2*X*Y*Z - 9*X*Z**2 - 5*Y**3 + 7*Y**2*Z + Y*Z**2 - Z**3
找到三个点,然后做如下的projective linear transformation,也就是换元法:
(X, x + 6983*y + 12786655623233*z)
(Y, x - 11207*y - 14559944854257*z)
(Z, x + 12440*y + 8189568859240*z)
得到这个方程:
128010669072400*x**2*z - 6018636259*x*y**2 - 11512137039155390218*x*y*z - 4920678109262728466907061459*x*z**2 - 3181797061512984297624468800000*y*z**2 - 6140495869762798292253643284262148800000*z**3
再去齐次化,得到:
128010669072400*x**2 - 6018636259*x*y**2 - 11512137039155390218*x*y - 4920678109262728466907061459*x - 3181797061512984297624468800000*y - 6140495869762798292253643284262148800000
这个方程乘以x,再做 xy --> y的替换,就基本上变成了Weierstrass形式。这一步不是线性的,而是有理的。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 10月 22日 16:03
由 TheMatrix
TheMatrix 写了: 2023年 10月 22日 15:54
用sympy算了一下。
假设椭圆曲线是一个一般三次曲线:
x**3 + 9*x**2*y + 4*x**2 - 5*x*y**2 - 2*x*y - 9*x - 5*y**3 + 7*y**2 + y - 1
齐次化:
X**3 + 9*X**2*Y + 4*X**2*Z - 5*X*Y**2 - 2*X*Y*Z - 9*X*Z**2 - 5*Y**3 + 7*Y**2*Z + Y*Z**2 - Z**3
找到三个点,然后做如下的projective linear transformation,也就是换元法:
(X, x + 6983*y + 12786655623233*z)
(Y, x - 11207*y - 14559944854257*z)
(Z, x + 12440*y + 8189568859240*z)
得到这个方程:
128010669072400*x**2*z - 6018636259*x*y**2 - 11512137039155390218*x*y*z - 4920678109262728466907061459*x*z**2 - 3181797061512984297624468800000*y*z**2 - 6140495869762798292253643284262148800000*z**3
再去齐次化,得到:
128010669072400*x**2 - 6018636259*x*y**2 - 11512137039155390218*x*y - 4920678109262728466907061459*x - 3181797061512984297624468800000*y - 6140495869762798292253643284262148800000
这个方程乘以x,再做 xy --> y的替换,就基本上变成了Weierstrass形式。这一步不是线性的,而是有理的。
不过这个只是为了证明一般三次曲线都能转化为Weierstrass标准形式。计算的话,应该不需要它。因为可以直接得到addition formula和duplication formula,比先转化为Weierstrass形式还简单。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 11月 20日 02:41
由 forecasting
这个帖子可以继续刷,不要沉下去了。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 11月 20日 11:50
由 TheMatrix
我UTM那本书都看完了。确实比GTM那本好理解得多。
GTM那本看完了7,8,9章 - local fields, global fields, integral points. 很多地方要先看UTM那本书,才知道它要干什么。
GTM那本现在在看第10章,Computing Mordell-Weil group。越到后面越技术化,group cohomology这些都出来了。还有作者自己的paper。然后是最后一章第11章,Elliptic Curve cryptography。这章在UTM那本书里也是有的。
后面这几章我没什么感觉了,可能是脑袋被摩擦的厉害,找不到感觉了。
有意义的是这么几块:
Integral points - 这个和Rational Points的方法很不同。
Computing Mordell-Weil group - 也就是Rank。
Elliptic Curve cryptography.
还有一块是L函数,这个在UTM里面讲到了,很有意思。GTM里面好像还没有。
我还没看完,还要再沉淀一下。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 11月 21日 14:56
由 Caravel
TheMatrix 写了: 2023年 11月 20日 11:50
我UTM那本书都看完了。确实比GTM那本好理解得多。
GTM那本看完了7,8,9章 - local fields, global fields, integral points. 很多地方要先看UTM那本书,才知道它要干什么。
GTM那本现在在看第10章,Computing Mordell-Weil group。越到后面越技术化,group cohomology这些都出来了。还有作者自己的paper。然后是最后一章第11章,Elliptic Curve cryptography。这章在UTM那本书里也是有的。
后面这几章我没什么感觉了,可能是脑袋被摩擦的厉害,找不到感觉了。
有意义的是这么几块:
Integral points - 这个和Rational Points的方法很不同。
Computing Mordell-Weil group - 也就是Rank。
Elliptic Curve cryptography.
还有一块是L函数,这个在UTM里面讲到了,很有意思。GTM里面好像还没有。
我还没看完,还要再沉淀一下。
你们还在啃这本书啊。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2023年 11月 21日 15:41
由 FoxMe
我最近一段时间没看了,但是以后还是会看的。有几个问题还没弄懂。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2024年 1月 18日 19:56
由 TheMatrix
TheMatrix 写了: 2023年 11月 20日 11:50
我UTM那本书都看完了。确实比GTM那本好理解得多。
GTM那本看完了7,8,9章 - local fields, global fields, integral points. 很多地方要先看UTM那本书,才知道它要干什么。
GTM那本现在在看第10章,Computing Mordell-Weil group。越到后面越技术化,group cohomology这些都出来了。还有作者自己的paper。然后是最后一章第11章,Elliptic Curve cryptography。这章在UTM那本书里也是有的。
后面这几章我没什么感觉了,可能是脑袋被摩擦的厉害,找不到感觉了。
有意义的是这么几块:
Integral points - 这个和Rational Points的方法很不同。
Computing Mordell-Weil group - 也就是Rank。
Elliptic Curve cryptography.
还有一块是L函数,这个在UTM里面讲到了,很有意思。GTM里面好像还没有。
我还没看完,还要再沉淀一下。
这本书确实有点难,后半部分很多无法领略。这两天和FoxMe,changbaihou讨论问题,才发现自己又miss一个点:
local-global principal
Tate–Shafarevich group
Hensel's lemma
local-global principal是说一个代数方程如果在所有的modulo p下有解,那么在Q下很可能有解。这里应该和Hensel's lemma也有关的 - 一个代数方程modulo p有解,那么modulo p
2也应该有解,same for p
n,所以在p-adic number中有解,也就是local field中有解。这是local-global中的local。
而Tate–Shafarevich group,是一种度量 - local-global principal不好使,或者说距离local-global principal好使有多远的一种度量 - obstruction of local-global principal。一般来讲,度量obstruction都是某种商群 - quotient,商去某种已知原理一定成立的情况。这种已知一定成立的情况,通常作为一个子群或者说kernel存在,商群就是coset,每一个都在这个子群的外面。coset有多少,就是这个商群,也就是这个obstruction的度量。Tate–Shafarevich group作为商群,我是听来的,先留个线头,有机会再了解。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2024年 1月 20日 17:25
由 FoxMe
0 → B(K)/f(A(K)) → Sel(f)(A/K) → Ш(A/K)[f] → 0
Selmer, Tate–Shafarevich group的定义需要cohomology,没学过,所以就没法往下看了。
Re: 关于椭圆曲线,听说这本书不错
发表于 : 2024年 3月 21日 07:47
由 forecasting
你们俩结束这学科或者这书的学习了吗?