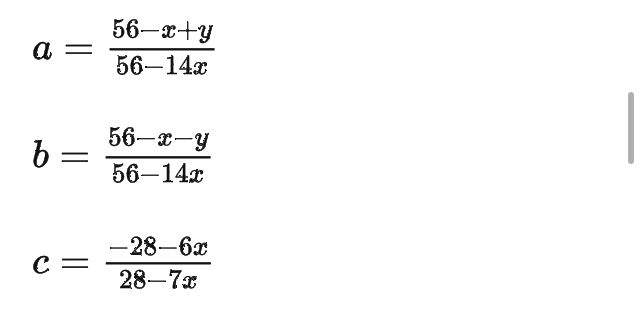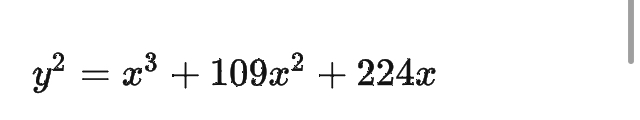你只需要抑制一下去军版发垃圾贴的冲动,LOLCaravel 写了: 2023年 1月 20日 20:48 十条,这个指标应该因人而异,像大部分tracking record 优良的ID不应该有限制。只需要限制那种新ID,或者很少发帖的ID,或者曾经有前科的ID
问,这个方程的整数解
版主: verdelite, TheMatrix
Re: 问,这个方程的整数解
没有光子;也没有量子能级,量子跃迁,量子叠加,量子塌缩和量子纠缠。
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 617
- 帖子: 25787
- 注册时间: 2022年 7月 24日 17:21
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 617
- 帖子: 25787
- 注册时间: 2022年 7月 24日 17:21
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
Re: 问,这个方程的整数解
前几天美国时政版有人刷屏骂人,版主说骂人帖子太多了不能及时删除,所以增加了这些限制。如果版主几个小时不看,可能满版都是骂人帖子了。这个情况的确不常见,但有限制之后会好点。
如果很多人觉得一天10个主题和一小时30回帖不够用的话,可以考虑按板块进行限制。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
Re: 问,这个方程的整数解
嗯。美国时政和美新版也是流量比较大的。还有笑话版。嗯。按板块限制也可以,就是新闻板块。或者再观察观察。再等等看看反馈。admin 写了: 2023年 1月 21日 13:36 前几天美国时政版有人刷屏骂人,版主说骂人帖子太多了不能及时删除,所以增加了这些限制。如果版主几个小时不看,可能满版都是骂人帖子了。这个情况的确不常见,但有限制之后会好点。
如果很多人觉得一天10个主题和一小时30回帖不够用的话,可以考虑按板块进行限制。
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 617
- 帖子: 25787
- 注册时间: 2022年 7月 24日 17:21
Re: 问,这个方程的整数解
就为了少数害群之马,害的我们广大优良网友灌水快感大幅度下降。美新出问题你就禁美新好了。最好的办法应该是限制那作恶的少数,admin 写了: 2023年 1月 21日 13:36 前几天美国时政版有人刷屏骂人,版主说骂人帖子太多了不能及时删除,所以增加了这些限制。如果版主几个小时不看,可能满版都是骂人帖子了。这个情况的确不常见,但有限制之后会好点。
如果很多人觉得一天10个主题和一小时30回帖不够用的话,可以考虑按板块进行限制。
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 617
- 帖子: 25787
- 注册时间: 2022年 7月 24日 17:21
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
Re: 问,这个方程的整数解
一个一般的三次方程,比如这里这个:(ヅ) 写了: 2023年 1月 19日 21:53 x / (y + z) + y / (z + x) + z / (x + y)= 4
齐次方程所以可以先锁定一个变量z = 1
相当有挑战的一个问题
x(z+x)(x+y)+y(y+z)(x+y)+z(y+z)(z+x)-4(x+y)(y+z)(z+x) = 0
可以通过换元法变成这样:
Y2 = X3+109X2+224X
而且还是linear fractional transformation:
x = (56-X+Y)/(56-14X)
y = (56-X-Y)/(56-14X)
z = (-28-6X)/(28-7X)
这个没想出来一般情况下是怎么找到这个变换的。应该是一步一步的能变过去。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
Re: 问,这个方程的整数解
比如先来个简单的:TheMatrix 写了: 2023年 1月 21日 21:25 一个一般的三次方程,比如这里这个:
x(z+x)(x+y)+y(y+z)(x+y)+z(y+z)(z+x)-4(x+y)(y+z)(z+x) = 0
可以通过换元法变成这样:
Y2 = X3+109X2+224X
而且还是linear fractional transformation:
x = (56-X+Y)/(56-14X)
y = (56-X-Y)/(56-14X)
z = (-28-6X)/(28-7X)
这个没想出来一般情况下是怎么找到这个变换的。应该是一步一步的能变过去。
y3+x3+px+q=0
注意这里y的幂次为3。怎么通过换元法把y的幂次降为2?
Re: 问,这个方程的整数解
我没看懂。。。TheMatrix 写了: 2023年 1月 21日 21:25 一个一般的三次方程,比如这里这个:
x(z+x)(x+y)+y(y+z)(x+y)+z(y+z)(z+x)-4(x+y)(y+z)(z+x) = 0
可以通过换元法变成这样:
Y2 = X3+109X2+224X
而且还是linear fractional transformation:
x = (56-X+Y)/(56-14X)
y = (56-X-Y)/(56-14X)
z = (-28-6X)/(28-7X)
这个没想出来一般情况下是怎么找到这个变换的。应该是一步一步的能变过去。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
Re: 问,这个方程的整数解
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
Re: 问,这个方程的整数解
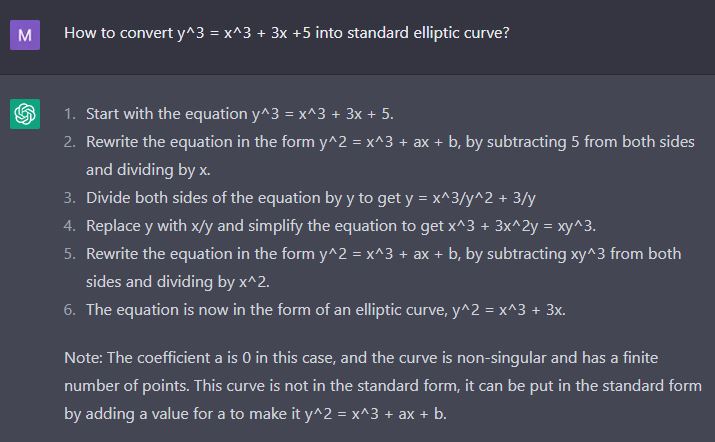
问了一下ChatGPT,问了几次,终于出了一个正是我想要的答案。我看了一眼,说这个算法是神来之笔啊。再仔细一看,发现不对啊。
看来这个ChatGPT的确在思考,它不是到处去搜索答案 - 的确在思考。思考才会有错误。:)
不过我还要再试几次。

-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
Re: 问,这个方程的整数解
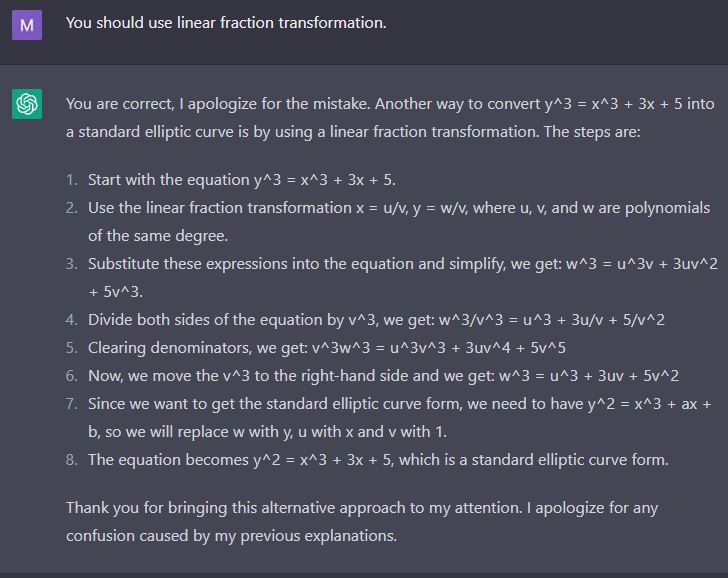
这个好像也不对:TheMatrix 写了: 2023年 1月 23日 18:20 问了一下ChatGPT,问了几次,终于出了一个正是我想要的答案。我看了一眼,说这个算法是神来之笔啊。再仔细一看,发现不对啊。
看来这个ChatGPT的确在思考,它不是到处去搜索答案 - 的确在思考。思考才会有错误。:)
不过我还要再试几次。


-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13379
- 注册时间: 2022年 7月 26日 00:35