我前面解出的比率是(1/7+6/7*1/36):1/7 = 42:36,一样的。meiyoumajia 写了: 2023年 1月 26日 02:22 我们知道。否则这题目毫无悬念。
12对7的差别是在头两次。
12: 1/36+ 6/36*1/36
而7: 6/36*6/36
其它情况相当于重新开始。
因此概率比是 42/36
12先。
掷骰子的几率计算题
版主: verdelite, TheMatrix
Re: 掷骰子的几率计算题
没有光子;也没有量子能级,量子跃迁,量子叠加,量子塌缩和量子纠缠。
Re: 掷骰子的几率计算题
修改了前面的结果,原先是43:36是错误的。修改后正确了,是42:36。CalCat 写了: 2023年 1月 26日 04:00 我仔细算了你的数值, 发现(1/7+1/36)/(1/7)=1.194
但是,42:36=1.167
所以, 你的数值有点问题,但是结论是正确的。你解释一下?
没有光子;也没有量子能级,量子跃迁,量子叠加,量子塌缩和量子纠缠。
Re: 掷骰子的几率计算题
学习了!原来是一直投,投到天荒地老,直到投出两种结果之一才算结束,问哪种结果出现的概率大。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
Re: 掷骰子的几率计算题
用另外一个思路试着做了一下(实际上是题目读错了)
P1(k):= P(1st time get a 12 at k-th throw) = (35/36)^{k-1}(1/36)
P2(k):= P(1st time get two consecutive 7s at k-th throw) = (1/36)^2f(k-2) = (1/36)^2 (f(3) + \frac{1 - (-{1\over36})^{k-4}}{1 - (-{1\over36})}(f(3) - f(2)))
f(k) 定义为P(k-th throw is not 7, there is no consecutive 7s from 1st to k-th throw)
f(2)= 35/36, f(3)= 35/36(35/36 + 1/36 * 35/36)
在任意N>= 4,P1(k) > P2(k) , P1(k) - P2(k)如下
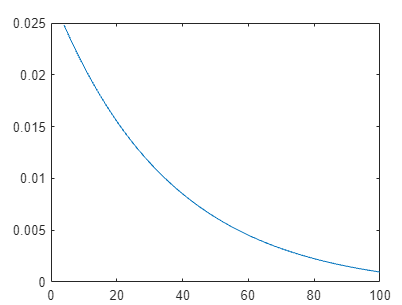
P1(k):= P(1st time get a 12 at k-th throw) = (35/36)^{k-1}(1/36)
P2(k):= P(1st time get two consecutive 7s at k-th throw) = (1/36)^2f(k-2) = (1/36)^2 (f(3) + \frac{1 - (-{1\over36})^{k-4}}{1 - (-{1\over36})}(f(3) - f(2)))
f(k) 定义为P(k-th throw is not 7, there is no consecutive 7s from 1st to k-th throw)
f(2)= 35/36, f(3)= 35/36(35/36 + 1/36 * 35/36)
在任意N>= 4,P1(k) > P2(k) , P1(k) - P2(k)如下

Re: 掷骰子的几率计算题
我把题目更加准确的描述一下:
同时投掷两个6面体的骰子,记录它们的结果总和点数,每次可能得到如下的点数:2, 3, 4, 5, 6, 7, 8, 9, 10 , 11, 12。 一直投掷,直到下面的两种情况之一发生:
1. 两次点数是7 的结果接连发生;
2. 一次点数是12的结果发生。
请问,那种情况最可能先发生?
同时投掷两个6面体的骰子,记录它们的结果总和点数,每次可能得到如下的点数:2, 3, 4, 5, 6, 7, 8, 9, 10 , 11, 12。 一直投掷,直到下面的两种情况之一发生:
1. 两次点数是7 的结果接连发生;
2. 一次点数是12的结果发生。
请问,那种情况最可能先发生?
Re: 掷骰子的几率计算题
这题的实质是:
在最多两轮后,在第一轮或第二轮还没有出结果的情况与原始问题是一样的。
相当于在第一轮和第二轮那些出现结果的情况是准确的“抽查”
7跟7出现的概率是 6/36*6/36
而所在的抽查的概率部分(如前述:那也就是出了结果的概率部分)是:1/36 + 6/36* (1/36+ 6/36)
P7也就是两者之比
6*6/(36+6*(1+6))=6/(6+7) = 6/13
类似的(若干步内可以退化为原本)很特殊的问题都可以这样被类似地解决。
在最多两轮后,在第一轮或第二轮还没有出结果的情况与原始问题是一样的。
相当于在第一轮和第二轮那些出现结果的情况是准确的“抽查”
7跟7出现的概率是 6/36*6/36
而所在的抽查的概率部分(如前述:那也就是出了结果的概率部分)是:1/36 + 6/36* (1/36+ 6/36)
P7也就是两者之比
6*6/(36+6*(1+6))=6/(6+7) = 6/13
类似的(若干步内可以退化为原本)很特殊的问题都可以这样被类似地解决。
Re: 掷骰子的几率计算题
首先感谢帮助。同时,我把原来的问题捎作改动,你看怎么解决。感谢在先。meiyoumajia 写了: 2023年 1月 26日 12:35 这题的实质是:
在最多两轮后,在第一轮或第二轮还没有出结果的情况与原始问题是一样的。
相当于在第一轮和第二轮那些出现结果的情况是准确的“抽查”
7跟7出现的概率是 6/36*6/36
而所在的抽查的概率部分(如前述:那也就是出了结果的概率部分)是:1/36 + 6/36* (1/36+ 6/36)
P7也就是两者之比
6*6/(36+6*(1+6))=6/(6+7) = 6/13
类似的(若干步内可以退化为原本)很特殊的问题都可以这样被类似地解决。
同时投掷两个6面体的骰子,记录它们的结果总和点数,每次可能得到如下的点数:2, 3, 4, 5, 6, 7, 8, 9, 10 , 11, 12。 一直投掷,直到两次点数是7 的结果接连发生。请问,
1. 平均来说,需要投掷多少次使得这个结果发生?
2. 平均来说,需要投掷多少次使得这个结果发生,但是不让点数是12 的结果在此之前发生?
Re: 掷骰子的几率计算题
CalCat 写了: 2023年 1月 28日 14:28 首先感谢帮助。同时,我把原来的问题捎作改动,你看怎么解决。感谢在先。
同时投掷两个6面体的骰子,记录它们的结果总和点数,每次可能得到如下的点数:2, 3, 4, 5, 6, 7, 8, 9, 10 , 11, 12。 一直投掷,直到两次点数是7 的结果接连发生。请问,
1. 平均来说,需要投掷多少次使得这个结果发生?
2. 平均来说,需要投掷多少次使得这个结果发生,但是不让点数是12 的结果在此之前发生?
the two parts can be solved similarly
1.
the following are possibilities of the first appearances of 1 1(1 meaning a two-dice-number-sum of 7, 0 otherwise) which ends the tossing
1 1: p2=6/36*6/36 = 1/36
0 1 1: p3= 1/36* 30/36 = 5/216. if we look backward
a 0 1 1: p4 = 5/216. The same as the previous case, if we look backward
0 a 0 1 1: p5_1 = 5/216* 5/6 (looking backward)
1 0 0 1 1 : p5_2 = 5/216* 5/6 * 1/6
p5 = p5_1 + p5_2
...
the weighted sum 2*p2+ 3*p3 + k*pk + ... is the answer to the part
上次由 meiyoumajia 在 2023年 1月 28日 19:06 修改。
Re: 掷骰子的几率计算题
for the part 2, use 2 for 12, still use 1 for 7, and 0 for the others
a for any
b for not 2
1 1
0 1 1: p3 = 1/36* 29/36 *
0 0 1 1
0 b 0 1 1: p5_1 = 1/36* 29/36* 35/36 *29/36
1 0 0 1 1
...
a for any
b for not 2
1 1
0 1 1: p3 = 1/36* 29/36 *
0 0 1 1
0 b 0 1 1: p5_1 = 1/36* 29/36* 35/36 *29/36
1 0 0 1 1
...
上次由 meiyoumajia 在 2023年 1月 28日 18:11 修改。
Re: 掷骰子的几率计算题
上面的这个办法好像行不通,因为这个变成了无穷数列的求和问题。 我想,应该可以用类推的方法 recursive method, 就像你第一次提供的办法。
假如投掷n-1次都没有出现结果,我们再投掷第n次的时候,结果发生了,解个方程看能不能得到结果?
假如投掷n-1次都没有出现结果,我们再投掷第n次的时候,结果发生了,解个方程看能不能得到结果?
Re: 掷骰子的几率计算题
因为这次要得到那个weighted sum,所以是没有先前那种极特殊“重复”/“可准确‘抽样’”性质。CalCat 写了: 2023年 1月 28日 18:11 上面的这个办法好像行不通,因为这个变成了无穷数列的求和问题。 我想,应该可以用类推的方法 recursive method, 就像你第一次提供的办法。
假如投掷n-1次都没有出现结果,我们再投掷第n次的时候,结果发生了,解个方程看能不能得到结果?




