(大妈出蹄)图形学:矩阵的第二个特征向量为何能用来分类
版主: verdelite, TheMatrix
Re: (大妈出蹄)图形学:矩阵的第二个特征向量为何能用来分类
"刚刚开始学习离散学和图像学。有个问题需要请教一下。
假设一个图形中有N个节点,组成一个N*N的相似矩阵(A)。
为什么矩阵A的第二个特征向量能用来分类?
mincut spectral partition"
这个矩阵A到底是啥矩阵?第二个特征值往往决定了spectral gap,很关键。第一个特征值有时是固定的,比如马尔可夫链的第一个(最大)特征值是1。还有图论里的Laplacian矩阵的第一个(最小)特征值是0. 估计大码指的是Laplacian,怎么会叫相似矩阵?
什么叫“离散学和图像学”?估计是离散数学和图论吧。
假设一个图形中有N个节点,组成一个N*N的相似矩阵(A)。
为什么矩阵A的第二个特征向量能用来分类?
mincut spectral partition"
这个矩阵A到底是啥矩阵?第二个特征值往往决定了spectral gap,很关键。第一个特征值有时是固定的,比如马尔可夫链的第一个(最大)特征值是1。还有图论里的Laplacian矩阵的第一个(最小)特征值是0. 估计大码指的是Laplacian,怎么会叫相似矩阵?
什么叫“离散学和图像学”?估计是离散数学和图论吧。
Re: (大妈出蹄)图形学:矩阵的第二个特征向量为何能用来分类
对,SVD可以通过特征分解来证明。但是何时用SVD,何时用特征分解?我个人理解是:
如果有相关A*A,就用特征分解(其实是两个SVD合起来);如果没有相关,只有一个孤零零的矩阵A,就用SVD(其实是半个特征分解)。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
-
harubashi(春橋)

- 著名点评

harubashi 的博客 - 帖子互动: 202
- 帖子: 3990
- 注册时间: 2022年 9月 6日 23:51
- 联系:
Re: (大妈出蹄)图形学:矩阵的第二个特征向量为何能用来分类
这个很简单啊,第一个特征向娘对应的是DC, all one, 特征值为0, 第二个是最优的分类,特征像娘是assignment index, 特征值是graph cut的cost,
-
harubashi(春橋)

- 著名点评

harubashi 的博客 - 帖子互动: 202
- 帖子: 3990
- 注册时间: 2022年 9月 6日 23:51
- 联系:
Re: (大妈出蹄)图形学:矩阵的第二个特征向量为何能用来分类
应该就是laplacian.FoxMe 写了: 2022年 12月 10日 09:43 "刚刚开始学习离散学和图像学。有个问题需要请教一下。
假设一个图形中有N个节点,组成一个N*N的相似矩阵(A)。
为什么矩阵A的第二个特征向量能用来分类?
mincut spectral partition"
这个矩阵A到底是啥矩阵?第二个特征值往往决定了spectral gap,很关键。第一个特征值有时是固定的,比如马尔可夫链的第一个(最大)特征值是1。还有图论里的Laplacian矩阵的第一个(最小)特征值是0. 估计大码指的是Laplacian,怎么会叫相似矩阵?
什么叫“离散学和图像学”?估计是离散数学和图论吧。
Re: (大妈出蹄)图形学:矩阵的第二个特征向量为何能用来分类
如果没人来解答,我来解答了。分几个问题回答,
1,大妈对付的是什么矩阵?按照她说的,图像上几个点,矩阵是图像的点相互间的相似矩阵。这个说明,不应该看成是图像处理问题;点也不是图像上的像素点。肯定不是计算机系搞图像处理的问题。那么她在说什么?我估计,是这样的:一个图,上面比如说有K个点。每个点代表一个病人,或者一个老鼠,或者一种水稻,等等。总之,一个点是一个subject,总共可能有几十、几百甚至几万个这样的点。这些subjects,有一些attributes,例如身高体重或者是各个基因位点的基因型,这些每个subjects之间都不同。然后,弄一个矩阵,KxK,entry i, j 代表两个subjects i, j之间相似性。
2,这是一个类似自相关矩阵的矩阵。可以做特征值分析,也就是Eigen analysis,也就是Principal component analyses. 其第一个特征向量为让各个subjects分离最远的投影方向,第二个特征向量是除第一个之外让各subjects分离最远的投影方向,第三个特征向量是除第一个第二个之外。。。如此类推。
3,如果这是一个自相关矩阵,那么第一个特征向量可以用来分类。原因在2里面说了。前几个都参与分类会分得更好。
4,如果第一个特征向量不能用来分类,那么原因是这不是一个自相关矩阵。在计算矩阵的时候没有进行过归一化,特别是没有去掉attributes的均值。这样计算出来,第一个特征向量代表把这些subjects分离最远的投影方向,一般情况下只是代表了这些attributes的均值。特殊情况下,均值接近0的时候,这各投影方向不一定是第一个特征向量方向,可能落到后面去了,这就和3情况类似了。
5,所以一般要对这些attributes进行减掉均值的预处理。一般还有除以标准差的预处理,这是所谓归一化。如果这些做了,那么就是3的情况。
例子:
你去下载个R,免费的,就可以跑我这个程序。
R
set.seed(3) #random seed
M=5; N=100 #2*M points, each has 100 attributes
P1=0.1+runif(N)*0.8; P2=0.1+runif(N)*0.8 #some point's attributes follow P1; some follow P2
data=matrix(0,2*M,N)
for(j in 1:N) {
data[2*(1:M)-1,j]=rbinom(5,1,P1[j]) #odd points follow P!
data[2*(1:M),j]=rbinom(5,1,P2[j]) #even points follow P2
}
#以上循环里面,奇数subjects的attributes依照P1给出的概率随机产生,偶数subjects的attributes依照P2给出的概率随机产生。
write.table(data,file="data.txt", col.names=T, row.names=F, quote=F, sep="")
#how the data looks like is at the end of the program; 2M rows, N cols
datasvd=svd(data) #svd of data matrix is e used to do Eigen analysis of "self similar" matrix
作图:
par(mfrow=c(2,2))
plot(datasvd$u[,1],datasvd$u[,2],col=c("blue","red"))
plot(datasvd$u[,2],datasvd$u[,3],col=c("blue","red"))
plot(datasvd$u[,3],datasvd$u[,4],col=c("blue","red"))
plot(datasvd$u[,4],datasvd$u[,5],col=c("blue","red"))
par(mfrow=c(1,1))
plot(datasvd$v[,1],colMeans(data),pch="*")
q()
data是像这个样子,
0100110010101010011001000011100110011000000100010100100100000010001000111101000011001000100101100101
1000100000010111100011100111110100100010001110011100001000110011101001000100110100001100010110101100
1110011111111111011110000101010000011101000100001110101111011110001000100101010111101100010001110000
0111100001101011101011110111010000000101001110110010111000001011100010011001011100000010000110011100
0100000111000010011000001111011010001110110110001100111100000111101110111100111111001100010111101000
1101000011001010110111110011110100100000011110011110111000011001101010101100110100000010000101111100
0110100110001110111101100111010001100100100010001100110100001010011100110111001111001001110000010001
0001010001111111111011001110011011111000001100010010001100101001111000100011010100010010010101111101
1100011011010111001011110101010000001011011100011001111100001010100110111111101111001100010001110001
1001010000101000110011111101111101100110101111100000001000001111101011101010100111100110001100001100
10行100列。10个subjects, 100个attributes。肉眼看不出来区别,但是奇数行和偶数行来自不同的parameters。
第一个图里面四个分图,是第1,2,3,4,5个特征向量相互之间scatter plot。
图上可见,第二个特征向量区分了奇数点和偶数点。
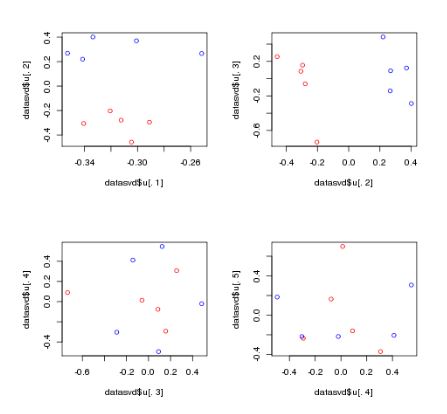
第二个图是第一个特征值对应的loading vector (v)(长度为N)和N个列均值之间的关系,表达了第一个特征向量和均值之间的关系。
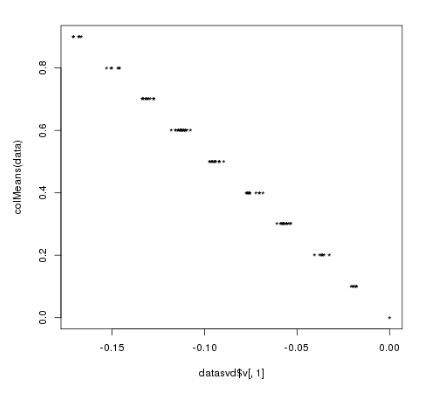
完
1,大妈对付的是什么矩阵?按照她说的,图像上几个点,矩阵是图像的点相互间的相似矩阵。这个说明,不应该看成是图像处理问题;点也不是图像上的像素点。肯定不是计算机系搞图像处理的问题。那么她在说什么?我估计,是这样的:一个图,上面比如说有K个点。每个点代表一个病人,或者一个老鼠,或者一种水稻,等等。总之,一个点是一个subject,总共可能有几十、几百甚至几万个这样的点。这些subjects,有一些attributes,例如身高体重或者是各个基因位点的基因型,这些每个subjects之间都不同。然后,弄一个矩阵,KxK,entry i, j 代表两个subjects i, j之间相似性。
2,这是一个类似自相关矩阵的矩阵。可以做特征值分析,也就是Eigen analysis,也就是Principal component analyses. 其第一个特征向量为让各个subjects分离最远的投影方向,第二个特征向量是除第一个之外让各subjects分离最远的投影方向,第三个特征向量是除第一个第二个之外。。。如此类推。
3,如果这是一个自相关矩阵,那么第一个特征向量可以用来分类。原因在2里面说了。前几个都参与分类会分得更好。
4,如果第一个特征向量不能用来分类,那么原因是这不是一个自相关矩阵。在计算矩阵的时候没有进行过归一化,特别是没有去掉attributes的均值。这样计算出来,第一个特征向量代表把这些subjects分离最远的投影方向,一般情况下只是代表了这些attributes的均值。特殊情况下,均值接近0的时候,这各投影方向不一定是第一个特征向量方向,可能落到后面去了,这就和3情况类似了。
5,所以一般要对这些attributes进行减掉均值的预处理。一般还有除以标准差的预处理,这是所谓归一化。如果这些做了,那么就是3的情况。
例子:
你去下载个R,免费的,就可以跑我这个程序。
R
set.seed(3) #random seed
M=5; N=100 #2*M points, each has 100 attributes
P1=0.1+runif(N)*0.8; P2=0.1+runif(N)*0.8 #some point's attributes follow P1; some follow P2
data=matrix(0,2*M,N)
for(j in 1:N) {
data[2*(1:M)-1,j]=rbinom(5,1,P1[j]) #odd points follow P!
data[2*(1:M),j]=rbinom(5,1,P2[j]) #even points follow P2
}
#以上循环里面,奇数subjects的attributes依照P1给出的概率随机产生,偶数subjects的attributes依照P2给出的概率随机产生。
write.table(data,file="data.txt", col.names=T, row.names=F, quote=F, sep="")
#how the data looks like is at the end of the program; 2M rows, N cols
datasvd=svd(data) #svd of data matrix is e used to do Eigen analysis of "self similar" matrix
作图:
par(mfrow=c(2,2))
plot(datasvd$u[,1],datasvd$u[,2],col=c("blue","red"))
plot(datasvd$u[,2],datasvd$u[,3],col=c("blue","red"))
plot(datasvd$u[,3],datasvd$u[,4],col=c("blue","red"))
plot(datasvd$u[,4],datasvd$u[,5],col=c("blue","red"))
par(mfrow=c(1,1))
plot(datasvd$v[,1],colMeans(data),pch="*")
q()
data是像这个样子,
0100110010101010011001000011100110011000000100010100100100000010001000111101000011001000100101100101
1000100000010111100011100111110100100010001110011100001000110011101001000100110100001100010110101100
1110011111111111011110000101010000011101000100001110101111011110001000100101010111101100010001110000
0111100001101011101011110111010000000101001110110010111000001011100010011001011100000010000110011100
0100000111000010011000001111011010001110110110001100111100000111101110111100111111001100010111101000
1101000011001010110111110011110100100000011110011110111000011001101010101100110100000010000101111100
0110100110001110111101100111010001100100100010001100110100001010011100110111001111001001110000010001
0001010001111111111011001110011011111000001100010010001100101001111000100011010100010010010101111101
1100011011010111001011110101010000001011011100011001111100001010100110111111101111001100010001110001
1001010000101000110011111101111101100110101111100000001000001111101011101010100111100110001100001100
10行100列。10个subjects, 100个attributes。肉眼看不出来区别,但是奇数行和偶数行来自不同的parameters。
第一个图里面四个分图,是第1,2,3,4,5个特征向量相互之间scatter plot。
图上可见,第二个特征向量区分了奇数点和偶数点。

第二个图是第一个特征值对应的loading vector (v)(长度为N)和N个列均值之间的关系,表达了第一个特征向量和均值之间的关系。

完
没有光子;也没有量子能级,量子跃迁,量子叠加,量子塌缩和量子纠缠。
Re: (大妈出蹄)图形学:矩阵的第二个特征向量为何能用来分类
我还以为你们会说出啥高级的数学来。
结果,你说的这个解答,是心理测量学里面的说法,算是达到了应用心理学人力资源管理专业的研究生的水平,但离心理测量专业研究生的水平还差很多。因为心理测量学研究生需要发这种文章:
Coefficient alpha and the internal structure of tests
Lee J. Cronbach
Psychometrika 16.3 (September 1951)
An index of factorial simplicity
Henry F. Kaiser
Psychometrika 39.1 (March 1974)
Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis
J. B. Kruskal
Psychometrika 29.1 (March 1964)
A reliability coefficient for maximum likelihood factor analysis
Ledyard R Tucker & Charles Lewis Tucker
Psychometrika 38.1 (March 1973)
The varimax criterion for analytic rotation in factor analysis
Henry F. Kaiser
Psychometrika 23.3 (September 1958)
A rationale and test for the number of factors in factor analysis
John L. Horn
Psychometrika 30.2 (June 1965)
Factor analysis and AIC
Hirotugu Akaike
Psychometrika 52.3 (September 1987)
On methods in the analysis of profile data
Samuel W. Greenhouse & Seymour Geisser
Psychometrika 24.2 (June 1959)
Nonmetric multidimensional scaling: A numerical method
J. B. Kruskal
Psychometrika 29.2 (June 1964)
Analysis of individual differences in multidimensional scaling via an n-way generalization of “Eckart-Young” decomposition
J. Douglas Carroll & Jih-Jie Chang
Psychometrika 35.3 (September 1970)
Hierarchical clustering schemes
Stephen C. Johnson
Psychometrika 32.2 (September 1967)
A scaled difference chi-square test statistic for moment structure analysis
Albert Satorra & Peter M. Bentler
Psychometrika 66.4 (December 2001)
Measurement invariance, factor analysis and factorial invariance
William Meredith
Psychometrika 58.4 (December 1993)
Model selection and Akaike's Information Criterion (AIC): The general theory and its analytical extensions
Hamparsum Bozdogan
Psychometrika 52.3 (September 1987)
An examination of procedures for determining the number of clusters in a data set
Glenn W. Milligan & Martha C. Cooper
Psychometrika 50.2 (June 1985)
Note on the sampling error of the difference between correlated proportions or percentages
Quinn McNemar
Psychometrika 12.2 (June 1947)
A rasch model for partial credit scoring
Geoff N. Masters
Psychometrika 47.2 (June 1982)
A second generation little jiffy
Henry F. Kaiser
Psychometrika 35.4 (December 1970)
Some mathematical notes on three-mode factor analysis
Ledyard R Tucker
Psychometrika 31.3 (September 1966)
Generalized procrustes analysis
J. C. Gower
Psychometrika 40.1 (March 1975)
The approximation of one matrix by another of lower rank
Carl Eckart & Gale Young
Psychometrika 1.3 (September 1936)
A rating formulation for ordered response categories
David Andrich
Psychometrika 43.4 (December 1978)
A new status index derived from sociometric analysis
Leo Katz
Psychometrika 18.1 (March 1953)
The analysis of proximities: Multidimensional scaling with an unknown distance function. I.
Roger N. Shepard
Psychometrika 27.2 (June 1962)
Estimation of latent ability using a response pattern of graded scores
Fumiko Samejima
Psychometrika 34.1 (March 1969)
Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm
R. Darrell Bock & Murray Aitkin
Psychometrika 46.4 (December 1981)
A general approach to confirmatory maximum likelihood factor analysis
K. G. Jöreskog
Psychometrika 34.2 (June 1969)
Determining the number of components from the matrix of partial correlations
Wayne F. Velicer
Psychometrika 41.3 (September 1976)
Multidimensional scaling: I. Theory and method
Warren S. Torgerson
Psychometrika 17.4 (December 1952)
A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators
Bengt Muthén
Psychometrika 49.1 (March 1984)
Application of model-selection criteria to some problems in multivariate analysis
Stanley L. Sclove
Psychometrika 52.3 (September 1987)
On the Use, the Misuse, and the Very Limited Usefulness of Cronbach’s Alpha
Klaas Sijtsma
Psychometrika 74.1 (March 2009)
Statistical analysis of sets of congeneric tests
K. G. Jöreskog
Psychometrika 36.2 (June 1971)
The centrality index of a graph
Gert Sabidussi
Psychometrika 31.4 (December 1966)
Simultaneous factor analysis in several populations
K. G. Jöreskog
Psychometrika 36.4 (December 1971)
A general nonmetric technique for finding the smallest coordinate space for a configuration of points
Louis Guttman
Psychometrika 33.4 (December 1968)
Latent curve analysis
William Meredith & John Tisak
Psychometrika 55.1 (March 1990)
The theory of the estimation of test reliability
G. F. Kuder & M. W. Richardson
Psychometrika 2.3 (September 1937)
A generalized solution of the orthogonal procrustes problem
Peter H. Schönemann
Psychometrika 31.1 (March 1966)
Some necessary conditions for common-factor analysis
Louis Guttman
Psychometrika 19.2 (June 1954)
The effect of sampling error on convergence, improper solutions, and goodness-of-fit indices for maximum likelihood confirmatory factor analysis
James C. Anderson & David W. Gerbing
Psychometrika 49.2 (June 1984)
The analysis of proximities: Multidimensional scaling with an unknown distance function. II
Roger N. Shepard
Psychometrika 27.3 (September 1962)
An examination of the effect of six types of error perturbation on fifteen clustering algorithms
Glenn W. Milligan
Psychometrika 45.3 (September 1980)
The development of hierarchical factor solutions
John Schmid & John M. Leiman
Psychometrika 22.1 (March 1957)
Estimation of the reliability of ratings
Robert L. Ebel
Psychometrika 16.4 (December 1951)
OpenMx: An Open Source Extended Structural Equation Modeling FrameworkSteven Boker, Michael Neale, Hermine Maes, Michael Wilde, Michael Spiegel, Timothy Brick, Jeffrey Spies, Ryne Estabrook, Sarah Kenny, Timothy Bates, Paras Mehta & John Fox
Psychometrika 76.2 (April 2011)
Estimating item parameters and latent ability when responses are scored in two or more nominal categories
R. Darrell Bock
Psychometrika 37.1 (March 1972)
Nonmetric individual differences multidimensional scaling: An alternating least squares method with optimal scaling features
Yoshio Takane, Forrest W. Young & Jan de Leeuw
Psychometrika 42.1 (March 1977)
Logit models and logistic regressions for social networks: I. An introduction to Markov graphs andp
Stanley Wasserman & Philippa Pattison
Psychometrika 61.3 (September 1996)
Maximum likelihood estimation of latent interaction effects with the LMS method
Andreas Klein & Helfried Moosbrugger
Psychometrika 65.4 (December 2000)
Latent variable modeling in heterogeneous populations
Bengt O. Muthén
Psychometrika 54.4 (September 1989)
Maximum likelihood estimation of the polychoric correlation coefficient
Ulf Olsson
Psychometrika 44.4 (December 1979)
Ensuring Positiveness of the Scaled Difference Chi-square Test Statistic
Albert Satorra & Peter M. Bentler
Psychometrika 75.2 (June 2010)
Cronbach’s α, Revelle’s β, and Mcdonald’s ω H : their relations with each other and two alternative conceptualizations of reliability
Richard E. Zinbarg, William Revelle, Iftah Yovel & Wen Li
Psychometrika 70.1 (March 2005)
Coefficients Alpha, Beta, Omega, and the glb: Comments on Sijtsma
William Revelle & Richard E. Zinbarg
Psychometrika 74.1 (March 2009)
Structural analysis of covariance and correlation matrices
Karl G. Jöreskog
Psychometrika 43.3 (December 1978)
A basis for analyzing test-retest reliability
Louis Guttman
Psychometrika 10.4 (December 1945)
On structural equation modeling with data that are not missing completely at random
Bengt Muthén, David Kaplan & Michael Hollis
Psychometrika 52.3 (September 1987)
Weighted likelihood estimation of ability in item response theory
Thomas A. Warm
Psychometrika 54.3 (September 1989)
Some contributions to maximum likelihood factor analysis
K. G. Jöreskog
Psychometrika 32.4 (December 1967)
A method of matrix analysis of group structure
R. Duncan Luce & Albert D. Perry
Psychometrika 14.2 (June 1949)
Time-limit tests: Estimating their reliability and degree of speeding
Lee J. Cronbach & W. G. Warrington
Psychometrika 16.2 (June 1951)
Redundancy analysis an alternative for canonical correlation analysis
Arnold L. van den Wollenberg
Psychometrika 42.2 (June 1977)
Principal component analysis of three-mode data by means of alternating least squares algorithms
Pieter M. Kroonenberg & Jan de Leeuw
Psychometrika 45.1 (March 1980)
The Bi-factor method
Karl J. Holzinger & Frances Swineford
Psychometrika 2.1 (March 1937)
Discussion of a set of points in terms of their mutual distances
Gale Young & A. S. Householder
Psychometrika 3.1 (March 1938)
Additive similarity trees
Shmuel Sattath & Amos Tversky
Psychometrika 42.3 (September 1977)
Generalized multilevel structural equation modeling
Sophia Rabe-Hesketh, Anders Skrondal & Andrew Pickles
Psychometrika 69.2 (June 2004)
On the relationship between item response theory and factor analysis of discretized variables
Yoshio Takane & Jan de Leeuw
Psychometrika 52.3 (September 1987)
Who belongs in the family?
Robert L. Thorndike
Psychometrika 18.4 (December 1953)
Multivariate information transmission
William J. McGill
Psychometrika 19.2 (June 1954)
Fitting a response model forn dichotomously scored items
R. Darrell Bock & Marcus Lieberman
Psychometrika 35.2 (June 1970)
Models for choice-reaction time
Mervyn Stone
Psychometrika 25.3 (September 1960)
Synthesis of variance
Franklin E. Satterthwaite
Psychometrika 6.5 (October 1941)
A method for simulating non-normal distributions
Allen I. Fleishman
Psychometrika 43.4 (December 1978)
Understanding correlates of change by modeling individual differences in growth
David R. Rogosa & John B. Willett
Psychometrika 50.2 (June 1985)
Linear programming techniques for multidimensional analysis of preferences
V. Srinivasan & Allan D. Shocker
Psychometrika 38.3 (September 1973)
A goodness of fit test for the rasch model
Erling B. Andersen
Psychometrika 38.1 (March 1973)
Coefficient alpha and the reliability of composite measurements
Melvin R. Novick & Charles Lewis
Psychometrika 32.1 (March 1967)
A sequential theory of psychological discrimination
S. W. Link & R. A. Heath
Psychometrika 40.1 (March 1975)
A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF
Robin Shealy & William Stout
Psychometrika 58.2 (June 1993)
Linear structural equations with latent variables
P. M. Bentler & David G. Weeks
Psychometrika 45.3 (September 1980)
Full-information item bi-factor analysis
Robert D. Gibbons & Donald R. Hedeker
Psychometrika 57.3 (September 1992)
Sensitivity of MRQAP Tests to Collinearity and Autocorrelation Conditions
David Dekker, David Krackhardt & Tom A. B. Snijders
Psychometrika 72.4 (December 2007)
Test reliability estimated by analysis of variance
Cyril Hoyt
Psychometrika 6.3 (June 1941)
On the multivariate asymptotic distribution of sequential Chi-square statistics
James H. Steiger, Alexander Shapiro & Michael W. Browne
Psychometrika 50.3 (September 1985)
Contributions to factor analysis of dichotomous variables
Bengt Muthén
Psychometrika 43.3 (December 1978)
Representation of structure in similarity data: Problems and prospects
Roger N. Shepard
Psychometrika 39.4 (December 1974)
A nonparametric approach for assessing latent trait unidimensionality
William Stout
Psychometrika 52.4 (December 1987)
OpenMx 2.0: Extended Structural Equation and Statistical Modeling
Michael C. Neale, Michael D. Hunter, Joshua N. Pritikin, Mahsa Zahery, Timothy R. Brick, Robert M. Kirkpatrick, Ryne Estabrook, Timothy C. Bates, Hermine H. Maes & Steven M. Boker
Psychometrika 81.2 (June 2016)
A least squares algorithm for fitting additive trees to proximity data
Geert De Soete
Psychometrika 48.4 (December 1983)
Alpha factor analysis
Henry F. Kaiser & John Caffrey
Psychometrika 30.1 (March 1965)
EM algorithms for ML factor analysis
Donald B. Rubin & Dorothy T. Thayer
Psychometrika 47.1 (March 1982)
Power of the likelihood ratio test in covariance structure analysis
Albert Satorra & Willem E. Saris
Psychometrika 50.1 (March 1985)
A dynamic factor model for the analysis of multivariate time series
Peter C. M. Molenaar
Psychometrika 50.2 (June 1985)
Orthogonal rotation to congruence
Norman Cliff
Psychometrika 31.1 (March 1966)
结果,你说的这个解答,是心理测量学里面的说法,算是达到了应用心理学人力资源管理专业的研究生的水平,但离心理测量专业研究生的水平还差很多。因为心理测量学研究生需要发这种文章:
Coefficient alpha and the internal structure of tests
Lee J. Cronbach
Psychometrika 16.3 (September 1951)
An index of factorial simplicity
Henry F. Kaiser
Psychometrika 39.1 (March 1974)
Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis
J. B. Kruskal
Psychometrika 29.1 (March 1964)
A reliability coefficient for maximum likelihood factor analysis
Ledyard R Tucker & Charles Lewis Tucker
Psychometrika 38.1 (March 1973)
The varimax criterion for analytic rotation in factor analysis
Henry F. Kaiser
Psychometrika 23.3 (September 1958)
A rationale and test for the number of factors in factor analysis
John L. Horn
Psychometrika 30.2 (June 1965)
Factor analysis and AIC
Hirotugu Akaike
Psychometrika 52.3 (September 1987)
On methods in the analysis of profile data
Samuel W. Greenhouse & Seymour Geisser
Psychometrika 24.2 (June 1959)
Nonmetric multidimensional scaling: A numerical method
J. B. Kruskal
Psychometrika 29.2 (June 1964)
Analysis of individual differences in multidimensional scaling via an n-way generalization of “Eckart-Young” decomposition
J. Douglas Carroll & Jih-Jie Chang
Psychometrika 35.3 (September 1970)
Hierarchical clustering schemes
Stephen C. Johnson
Psychometrika 32.2 (September 1967)
A scaled difference chi-square test statistic for moment structure analysis
Albert Satorra & Peter M. Bentler
Psychometrika 66.4 (December 2001)
Measurement invariance, factor analysis and factorial invariance
William Meredith
Psychometrika 58.4 (December 1993)
Model selection and Akaike's Information Criterion (AIC): The general theory and its analytical extensions
Hamparsum Bozdogan
Psychometrika 52.3 (September 1987)
An examination of procedures for determining the number of clusters in a data set
Glenn W. Milligan & Martha C. Cooper
Psychometrika 50.2 (June 1985)
Note on the sampling error of the difference between correlated proportions or percentages
Quinn McNemar
Psychometrika 12.2 (June 1947)
A rasch model for partial credit scoring
Geoff N. Masters
Psychometrika 47.2 (June 1982)
A second generation little jiffy
Henry F. Kaiser
Psychometrika 35.4 (December 1970)
Some mathematical notes on three-mode factor analysis
Ledyard R Tucker
Psychometrika 31.3 (September 1966)
Generalized procrustes analysis
J. C. Gower
Psychometrika 40.1 (March 1975)
The approximation of one matrix by another of lower rank
Carl Eckart & Gale Young
Psychometrika 1.3 (September 1936)
A rating formulation for ordered response categories
David Andrich
Psychometrika 43.4 (December 1978)
A new status index derived from sociometric analysis
Leo Katz
Psychometrika 18.1 (March 1953)
The analysis of proximities: Multidimensional scaling with an unknown distance function. I.
Roger N. Shepard
Psychometrika 27.2 (June 1962)
Estimation of latent ability using a response pattern of graded scores
Fumiko Samejima
Psychometrika 34.1 (March 1969)
Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm
R. Darrell Bock & Murray Aitkin
Psychometrika 46.4 (December 1981)
A general approach to confirmatory maximum likelihood factor analysis
K. G. Jöreskog
Psychometrika 34.2 (June 1969)
Determining the number of components from the matrix of partial correlations
Wayne F. Velicer
Psychometrika 41.3 (September 1976)
Multidimensional scaling: I. Theory and method
Warren S. Torgerson
Psychometrika 17.4 (December 1952)
A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators
Bengt Muthén
Psychometrika 49.1 (March 1984)
Application of model-selection criteria to some problems in multivariate analysis
Stanley L. Sclove
Psychometrika 52.3 (September 1987)
On the Use, the Misuse, and the Very Limited Usefulness of Cronbach’s Alpha
Klaas Sijtsma
Psychometrika 74.1 (March 2009)
Statistical analysis of sets of congeneric tests
K. G. Jöreskog
Psychometrika 36.2 (June 1971)
The centrality index of a graph
Gert Sabidussi
Psychometrika 31.4 (December 1966)
Simultaneous factor analysis in several populations
K. G. Jöreskog
Psychometrika 36.4 (December 1971)
A general nonmetric technique for finding the smallest coordinate space for a configuration of points
Louis Guttman
Psychometrika 33.4 (December 1968)
Latent curve analysis
William Meredith & John Tisak
Psychometrika 55.1 (March 1990)
The theory of the estimation of test reliability
G. F. Kuder & M. W. Richardson
Psychometrika 2.3 (September 1937)
A generalized solution of the orthogonal procrustes problem
Peter H. Schönemann
Psychometrika 31.1 (March 1966)
Some necessary conditions for common-factor analysis
Louis Guttman
Psychometrika 19.2 (June 1954)
The effect of sampling error on convergence, improper solutions, and goodness-of-fit indices for maximum likelihood confirmatory factor analysis
James C. Anderson & David W. Gerbing
Psychometrika 49.2 (June 1984)
The analysis of proximities: Multidimensional scaling with an unknown distance function. II
Roger N. Shepard
Psychometrika 27.3 (September 1962)
An examination of the effect of six types of error perturbation on fifteen clustering algorithms
Glenn W. Milligan
Psychometrika 45.3 (September 1980)
The development of hierarchical factor solutions
John Schmid & John M. Leiman
Psychometrika 22.1 (March 1957)
Estimation of the reliability of ratings
Robert L. Ebel
Psychometrika 16.4 (December 1951)
OpenMx: An Open Source Extended Structural Equation Modeling FrameworkSteven Boker, Michael Neale, Hermine Maes, Michael Wilde, Michael Spiegel, Timothy Brick, Jeffrey Spies, Ryne Estabrook, Sarah Kenny, Timothy Bates, Paras Mehta & John Fox
Psychometrika 76.2 (April 2011)
Estimating item parameters and latent ability when responses are scored in two or more nominal categories
R. Darrell Bock
Psychometrika 37.1 (March 1972)
Nonmetric individual differences multidimensional scaling: An alternating least squares method with optimal scaling features
Yoshio Takane, Forrest W. Young & Jan de Leeuw
Psychometrika 42.1 (March 1977)
Logit models and logistic regressions for social networks: I. An introduction to Markov graphs andp
Stanley Wasserman & Philippa Pattison
Psychometrika 61.3 (September 1996)
Maximum likelihood estimation of latent interaction effects with the LMS method
Andreas Klein & Helfried Moosbrugger
Psychometrika 65.4 (December 2000)
Latent variable modeling in heterogeneous populations
Bengt O. Muthén
Psychometrika 54.4 (September 1989)
Maximum likelihood estimation of the polychoric correlation coefficient
Ulf Olsson
Psychometrika 44.4 (December 1979)
Ensuring Positiveness of the Scaled Difference Chi-square Test Statistic
Albert Satorra & Peter M. Bentler
Psychometrika 75.2 (June 2010)
Cronbach’s α, Revelle’s β, and Mcdonald’s ω H : their relations with each other and two alternative conceptualizations of reliability
Richard E. Zinbarg, William Revelle, Iftah Yovel & Wen Li
Psychometrika 70.1 (March 2005)
Coefficients Alpha, Beta, Omega, and the glb: Comments on Sijtsma
William Revelle & Richard E. Zinbarg
Psychometrika 74.1 (March 2009)
Structural analysis of covariance and correlation matrices
Karl G. Jöreskog
Psychometrika 43.3 (December 1978)
A basis for analyzing test-retest reliability
Louis Guttman
Psychometrika 10.4 (December 1945)
On structural equation modeling with data that are not missing completely at random
Bengt Muthén, David Kaplan & Michael Hollis
Psychometrika 52.3 (September 1987)
Weighted likelihood estimation of ability in item response theory
Thomas A. Warm
Psychometrika 54.3 (September 1989)
Some contributions to maximum likelihood factor analysis
K. G. Jöreskog
Psychometrika 32.4 (December 1967)
A method of matrix analysis of group structure
R. Duncan Luce & Albert D. Perry
Psychometrika 14.2 (June 1949)
Time-limit tests: Estimating their reliability and degree of speeding
Lee J. Cronbach & W. G. Warrington
Psychometrika 16.2 (June 1951)
Redundancy analysis an alternative for canonical correlation analysis
Arnold L. van den Wollenberg
Psychometrika 42.2 (June 1977)
Principal component analysis of three-mode data by means of alternating least squares algorithms
Pieter M. Kroonenberg & Jan de Leeuw
Psychometrika 45.1 (March 1980)
The Bi-factor method
Karl J. Holzinger & Frances Swineford
Psychometrika 2.1 (March 1937)
Discussion of a set of points in terms of their mutual distances
Gale Young & A. S. Householder
Psychometrika 3.1 (March 1938)
Additive similarity trees
Shmuel Sattath & Amos Tversky
Psychometrika 42.3 (September 1977)
Generalized multilevel structural equation modeling
Sophia Rabe-Hesketh, Anders Skrondal & Andrew Pickles
Psychometrika 69.2 (June 2004)
On the relationship between item response theory and factor analysis of discretized variables
Yoshio Takane & Jan de Leeuw
Psychometrika 52.3 (September 1987)
Who belongs in the family?
Robert L. Thorndike
Psychometrika 18.4 (December 1953)
Multivariate information transmission
William J. McGill
Psychometrika 19.2 (June 1954)
Fitting a response model forn dichotomously scored items
R. Darrell Bock & Marcus Lieberman
Psychometrika 35.2 (June 1970)
Models for choice-reaction time
Mervyn Stone
Psychometrika 25.3 (September 1960)
Synthesis of variance
Franklin E. Satterthwaite
Psychometrika 6.5 (October 1941)
A method for simulating non-normal distributions
Allen I. Fleishman
Psychometrika 43.4 (December 1978)
Understanding correlates of change by modeling individual differences in growth
David R. Rogosa & John B. Willett
Psychometrika 50.2 (June 1985)
Linear programming techniques for multidimensional analysis of preferences
V. Srinivasan & Allan D. Shocker
Psychometrika 38.3 (September 1973)
A goodness of fit test for the rasch model
Erling B. Andersen
Psychometrika 38.1 (March 1973)
Coefficient alpha and the reliability of composite measurements
Melvin R. Novick & Charles Lewis
Psychometrika 32.1 (March 1967)
A sequential theory of psychological discrimination
S. W. Link & R. A. Heath
Psychometrika 40.1 (March 1975)
A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF
Robin Shealy & William Stout
Psychometrika 58.2 (June 1993)
Linear structural equations with latent variables
P. M. Bentler & David G. Weeks
Psychometrika 45.3 (September 1980)
Full-information item bi-factor analysis
Robert D. Gibbons & Donald R. Hedeker
Psychometrika 57.3 (September 1992)
Sensitivity of MRQAP Tests to Collinearity and Autocorrelation Conditions
David Dekker, David Krackhardt & Tom A. B. Snijders
Psychometrika 72.4 (December 2007)
Test reliability estimated by analysis of variance
Cyril Hoyt
Psychometrika 6.3 (June 1941)
On the multivariate asymptotic distribution of sequential Chi-square statistics
James H. Steiger, Alexander Shapiro & Michael W. Browne
Psychometrika 50.3 (September 1985)
Contributions to factor analysis of dichotomous variables
Bengt Muthén
Psychometrika 43.3 (December 1978)
Representation of structure in similarity data: Problems and prospects
Roger N. Shepard
Psychometrika 39.4 (December 1974)
A nonparametric approach for assessing latent trait unidimensionality
William Stout
Psychometrika 52.4 (December 1987)
OpenMx 2.0: Extended Structural Equation and Statistical Modeling
Michael C. Neale, Michael D. Hunter, Joshua N. Pritikin, Mahsa Zahery, Timothy R. Brick, Robert M. Kirkpatrick, Ryne Estabrook, Timothy C. Bates, Hermine H. Maes & Steven M. Boker
Psychometrika 81.2 (June 2016)
A least squares algorithm for fitting additive trees to proximity data
Geert De Soete
Psychometrika 48.4 (December 1983)
Alpha factor analysis
Henry F. Kaiser & John Caffrey
Psychometrika 30.1 (March 1965)
EM algorithms for ML factor analysis
Donald B. Rubin & Dorothy T. Thayer
Psychometrika 47.1 (March 1982)
Power of the likelihood ratio test in covariance structure analysis
Albert Satorra & Willem E. Saris
Psychometrika 50.1 (March 1985)
A dynamic factor model for the analysis of multivariate time series
Peter C. M. Molenaar
Psychometrika 50.2 (June 1985)
Orthogonal rotation to congruence
Norman Cliff
Psychometrika 31.1 (March 1966)
verdelite 写了: 2022年 12月 13日 15:38 如果没人来解答,我来解答了。分几个问题回答,
1,大妈对付的是什么矩阵?按照她说的,图像上几个点,矩阵是图像的点相互间的相似矩阵。这个说明,不应该看成是图像处理问题;点也不是图像上的像素点。肯定不是计算机系搞图像处理的问题。那么她在说什么?我估计,是这样的:一个图,上面比如说有K个点。每个点代表一个病人,或者一个老鼠,或者一种水稻,等等。总之,一个点是一个subject,总共可能有几十、几百甚至几万个这样的点。这些subjects,有一些attributes,例如身高体重或者是各个基因位点的基因型,这些每个subjects之间都不同。然后,弄一个矩阵,KxK,entry i, j 代表两个subjects i, j之间相似性。
2,这是一个类似自相关矩阵的矩阵。可以做特征值分析,也就是Eigen analysis,也就是Principal component analyses. 其第一个特征向量为让各个subjects分离最远的投影方向,第二个特征向量是除第一个之外让各subjects分离最远的投影方向,第三个特征向量是除第一个第二个之外。。。如此类推。
3,如果这是一个自相关矩阵,那么第一个特征向量可以用来分类。原因在2里面说了。前几个都参与分类会分得更好。
4,如果第一个特征向量不能用来分类,那么原因是这不是一个自相关矩阵。在计算矩阵的时候没有进行过归一化,特别是没有去掉attributes的均值。这样计算出来,第一个特征向量代表把这些subjects分离最远的投影方向,一般情况下只是代表了这些attributes的均值。特殊情况下,均值接近0的时候,这各投影方向不一定是第一个特征向量方向,可能落到后面去了,这就和3情况类似了。
5,所以一般要对这些attributes进行减掉均值的预处理。一般还有除以标准差的预处理,这是所谓归一化。如果这些做了,那么就是3的情况。
例子:
你去下载个R,免费的,就可以跑我这个程序。
R
set.seed(3) #random seed
M=5; N=100 #2*M points, each has 100 attributes
P1=0.1+runif(N)*0.8; P2=0.1+runif(N)*0.8 #some point's attributes follow P1; some follow P2
data=matrix(0,2*M,N)
for(j in 1:N) {
data[2*(1:M)-1,j]=rbinom(5,1,P1[j]) #odd points follow P!
data[2*(1:M),j]=rbinom(5,1,P2[j]) #even points follow P2
}
#以上循环里面,奇数subjects的attributes依照P1给出的概率随机产生,偶数subjects的attributes依照P2给出的概率随机产生。
write.table(data,file="data.txt", col.names=T, row.names=F, quote=F, sep="")
#how the data looks like is at the end of the program; 2M rows, N cols
datasvd=svd(data) #svd of data matrix is e used to do Eigen analysis of "self similar" matrix
作图:
par(mfrow=c(2,2))
plot(datasvd$u[,1],datasvd$u[,2],col=c("blue","red"))
plot(datasvd$u[,2],datasvd$u[,3],col=c("blue","red"))
plot(datasvd$u[,3],datasvd$u[,4],col=c("blue","red"))
plot(datasvd$u[,4],datasvd$u[,5],col=c("blue","red"))
par(mfrow=c(1,1))
plot(datasvd$v[,1],colMeans(data),pch="*")
q()
data是像这个样子,
0100110010101010011001000011100110011000000100010100100100000010001000111101000011001000100101100101
1000100000010111100011100111110100100010001110011100001000110011101001000100110100001100010110101100
1110011111111111011110000101010000011101000100001110101111011110001000100101010111101100010001110000
0111100001101011101011110111010000000101001110110010111000001011100010011001011100000010000110011100
0100000111000010011000001111011010001110110110001100111100000111101110111100111111001100010111101000
1101000011001010110111110011110100100000011110011110111000011001101010101100110100000010000101111100
0110100110001110111101100111010001100100100010001100110100001010011100110111001111001001110000010001
0001010001111111111011001110011011111000001100010010001100101001111000100011010100010010010101111101
1100011011010111001011110101010000001011011100011001111100001010100110111111101111001100010001110001
1001010000101000110011111101111101100110101111100000001000001111101011101010100111100110001100001100
10行100列。10个subjects, 100个attributes。肉眼看不出来区别,但是奇数行和偶数行来自不同的parameters。
第一个图里面四个分图,是第1,2,3,4,5个特征向量相互之间scatter plot。
图上可见,第二个特征向量区分了奇数点和偶数点。
第二个图是第一个特征值对应的loading vector (v)(长度为N)和N个列均值之间的关系,表达了第一个特征向量和均值之间的关系。
完
Re: (大妈出蹄)图形学:矩阵的第二个特征向量为何能用来分类
你这么牛,你咋不回答。这问题挂这儿几个月了。hci 写了: 2022年 12月 13日 17:06 我还以为你们会说出啥高级的数学来。
结果,你说的这个解答,是心理测量学里面的说法,算是达到了应用心理学人力资源管理专业的研究生的水平,但离心理测量专业研究生的水平还差很多。因为心理测量学研究生需要发这种文章:
Coefficient alpha and the internal structure of tests
Lee J. Cronbach
Psychometrika 16.3 (September 1951)
An index of factorial simplicity
Henry F. Kaiser
Psychometrika 39.1 (March 1974)
Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis
J. B. Kruskal
Psychometrika 29.1 (March 1964)
A reliability coefficient for maximum likelihood factor analysis
Ledyard R Tucker & Charles Lewis Tucker
Psychometrika 38.1 (March 1973)
The varimax criterion for analytic rotation in factor analysis
Henry F. Kaiser
Psychometrika 23.3 (September 1958)
A rationale and test for the number of factors in factor analysis
John L. Horn
Psychometrika 30.2 (June 1965)
Factor analysis and AIC
Hirotugu Akaike
Psychometrika 52.3 (September 1987)
On methods in the analysis of profile data
Samuel W. Greenhouse & Seymour Geisser
Psychometrika 24.2 (June 1959)
Nonmetric multidimensional scaling: A numerical method
J. B. Kruskal
Psychometrika 29.2 (June 1964)
Analysis of individual differences in multidimensional scaling via an n-way generalization of “Eckart-Young” decomposition
J. Douglas Carroll & Jih-Jie Chang
Psychometrika 35.3 (September 1970)
Hierarchical clustering schemes
Stephen C. Johnson
Psychometrika 32.2 (September 1967)
A scaled difference chi-square test statistic for moment structure analysis
Albert Satorra & Peter M. Bentler
Psychometrika 66.4 (December 2001)
Measurement invariance, factor analysis and factorial invariance
William Meredith
Psychometrika 58.4 (December 1993)
Model selection and Akaike's Information Criterion (AIC): The general theory and its analytical extensions
Hamparsum Bozdogan
Psychometrika 52.3 (September 1987)
An examination of procedures for determining the number of clusters in a data set
Glenn W. Milligan & Martha C. Cooper
Psychometrika 50.2 (June 1985)
Note on the sampling error of the difference between correlated proportions or percentages
Quinn McNemar
Psychometrika 12.2 (June 1947)
A rasch model for partial credit scoring
Geoff N. Masters
Psychometrika 47.2 (June 1982)
A second generation little jiffy
Henry F. Kaiser
Psychometrika 35.4 (December 1970)
Some mathematical notes on three-mode factor analysis
Ledyard R Tucker
Psychometrika 31.3 (September 1966)
Generalized procrustes analysis
J. C. Gower
Psychometrika 40.1 (March 1975)
The approximation of one matrix by another of lower rank
Carl Eckart & Gale Young
Psychometrika 1.3 (September 1936)
A rating formulation for ordered response categories
David Andrich
Psychometrika 43.4 (December 1978)
A new status index derived from sociometric analysis
Leo Katz
Psychometrika 18.1 (March 1953)
The analysis of proximities: Multidimensional scaling with an unknown distance function. I.
Roger N. Shepard
Psychometrika 27.2 (June 1962)
Estimation of latent ability using a response pattern of graded scores
Fumiko Samejima
Psychometrika 34.1 (March 1969)
Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm
R. Darrell Bock & Murray Aitkin
Psychometrika 46.4 (December 1981)
A general approach to confirmatory maximum likelihood factor analysis
K. G. Jöreskog
Psychometrika 34.2 (June 1969)
Determining the number of components from the matrix of partial correlations
Wayne F. Velicer
Psychometrika 41.3 (September 1976)
Multidimensional scaling: I. Theory and method
Warren S. Torgerson
Psychometrika 17.4 (December 1952)
A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators
Bengt Muthén
Psychometrika 49.1 (March 1984)
Application of model-selection criteria to some problems in multivariate analysis
Stanley L. Sclove
Psychometrika 52.3 (September 1987)
On the Use, the Misuse, and the Very Limited Usefulness of Cronbach’s Alpha
Klaas Sijtsma
Psychometrika 74.1 (March 2009)
Statistical analysis of sets of congeneric tests
K. G. Jöreskog
Psychometrika 36.2 (June 1971)
The centrality index of a graph
Gert Sabidussi
Psychometrika 31.4 (December 1966)
Simultaneous factor analysis in several populations
K. G. Jöreskog
Psychometrika 36.4 (December 1971)
A general nonmetric technique for finding the smallest coordinate space for a configuration of points
Louis Guttman
Psychometrika 33.4 (December 1968)
Latent curve analysis
William Meredith & John Tisak
Psychometrika 55.1 (March 1990)
The theory of the estimation of test reliability
G. F. Kuder & M. W. Richardson
Psychometrika 2.3 (September 1937)
A generalized solution of the orthogonal procrustes problem
Peter H. Schönemann
Psychometrika 31.1 (March 1966)
Some necessary conditions for common-factor analysis
Louis Guttman
Psychometrika 19.2 (June 1954)
The effect of sampling error on convergence, improper solutions, and goodness-of-fit indices for maximum likelihood confirmatory factor analysis
James C. Anderson & David W. Gerbing
Psychometrika 49.2 (June 1984)
The analysis of proximities: Multidimensional scaling with an unknown distance function. II
Roger N. Shepard
Psychometrika 27.3 (September 1962)
An examination of the effect of six types of error perturbation on fifteen clustering algorithms
Glenn W. Milligan
Psychometrika 45.3 (September 1980)
The development of hierarchical factor solutions
John Schmid & John M. Leiman
Psychometrika 22.1 (March 1957)
Estimation of the reliability of ratings
Robert L. Ebel
Psychometrika 16.4 (December 1951)
OpenMx: An Open Source Extended Structural Equation Modeling FrameworkSteven Boker, Michael Neale, Hermine Maes, Michael Wilde, Michael Spiegel, Timothy Brick, Jeffrey Spies, Ryne Estabrook, Sarah Kenny, Timothy Bates, Paras Mehta & John Fox
Psychometrika 76.2 (April 2011)
Estimating item parameters and latent ability when responses are scored in two or more nominal categories
R. Darrell Bock
Psychometrika 37.1 (March 1972)
Nonmetric individual differences multidimensional scaling: An alternating least squares method with optimal scaling features
Yoshio Takane, Forrest W. Young & Jan de Leeuw
Psychometrika 42.1 (March 1977)
Logit models and logistic regressions for social networks: I. An introduction to Markov graphs andp
Stanley Wasserman & Philippa Pattison
Psychometrika 61.3 (September 1996)
Maximum likelihood estimation of latent interaction effects with the LMS method
Andreas Klein & Helfried Moosbrugger
Psychometrika 65.4 (December 2000)
Latent variable modeling in heterogeneous populations
Bengt O. Muthén
Psychometrika 54.4 (September 1989)
Maximum likelihood estimation of the polychoric correlation coefficient
Ulf Olsson
Psychometrika 44.4 (December 1979)
Ensuring Positiveness of the Scaled Difference Chi-square Test Statistic
Albert Satorra & Peter M. Bentler
Psychometrika 75.2 (June 2010)
Cronbach’s α, Revelle’s β, and Mcdonald’s ω H : their relations with each other and two alternative conceptualizations of reliability
Richard E. Zinbarg, William Revelle, Iftah Yovel & Wen Li
Psychometrika 70.1 (March 2005)
Coefficients Alpha, Beta, Omega, and the glb: Comments on Sijtsma
William Revelle & Richard E. Zinbarg
Psychometrika 74.1 (March 2009)
Structural analysis of covariance and correlation matrices
Karl G. Jöreskog
Psychometrika 43.3 (December 1978)
A basis for analyzing test-retest reliability
Louis Guttman
Psychometrika 10.4 (December 1945)
On structural equation modeling with data that are not missing completely at random
Bengt Muthén, David Kaplan & Michael Hollis
Psychometrika 52.3 (September 1987)
Weighted likelihood estimation of ability in item response theory
Thomas A. Warm
Psychometrika 54.3 (September 1989)
Some contributions to maximum likelihood factor analysis
K. G. Jöreskog
Psychometrika 32.4 (December 1967)
A method of matrix analysis of group structure
R. Duncan Luce & Albert D. Perry
Psychometrika 14.2 (June 1949)
Time-limit tests: Estimating their reliability and degree of speeding
Lee J. Cronbach & W. G. Warrington
Psychometrika 16.2 (June 1951)
Redundancy analysis an alternative for canonical correlation analysis
Arnold L. van den Wollenberg
Psychometrika 42.2 (June 1977)
Principal component analysis of three-mode data by means of alternating least squares algorithms
Pieter M. Kroonenberg & Jan de Leeuw
Psychometrika 45.1 (March 1980)
The Bi-factor method
Karl J. Holzinger & Frances Swineford
Psychometrika 2.1 (March 1937)
Discussion of a set of points in terms of their mutual distances
Gale Young & A. S. Householder
Psychometrika 3.1 (March 1938)
Additive similarity trees
Shmuel Sattath & Amos Tversky
Psychometrika 42.3 (September 1977)
Generalized multilevel structural equation modeling
Sophia Rabe-Hesketh, Anders Skrondal & Andrew Pickles
Psychometrika 69.2 (June 2004)
On the relationship between item response theory and factor analysis of discretized variables
Yoshio Takane & Jan de Leeuw
Psychometrika 52.3 (September 1987)
Who belongs in the family?
Robert L. Thorndike
Psychometrika 18.4 (December 1953)
Multivariate information transmission
William J. McGill
Psychometrika 19.2 (June 1954)
Fitting a response model forn dichotomously scored items
R. Darrell Bock & Marcus Lieberman
Psychometrika 35.2 (June 1970)
Models for choice-reaction time
Mervyn Stone
Psychometrika 25.3 (September 1960)
Synthesis of variance
Franklin E. Satterthwaite
Psychometrika 6.5 (October 1941)
A method for simulating non-normal distributions
Allen I. Fleishman
Psychometrika 43.4 (December 1978)
Understanding correlates of change by modeling individual differences in growth
David R. Rogosa & John B. Willett
Psychometrika 50.2 (June 1985)
Linear programming techniques for multidimensional analysis of preferences
V. Srinivasan & Allan D. Shocker
Psychometrika 38.3 (September 1973)
A goodness of fit test for the rasch model
Erling B. Andersen
Psychometrika 38.1 (March 1973)
Coefficient alpha and the reliability of composite measurements
Melvin R. Novick & Charles Lewis
Psychometrika 32.1 (March 1967)
A sequential theory of psychological discrimination
S. W. Link & R. A. Heath
Psychometrika 40.1 (March 1975)
A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF
Robin Shealy & William Stout
Psychometrika 58.2 (June 1993)
Linear structural equations with latent variables
P. M. Bentler & David G. Weeks
Psychometrika 45.3 (September 1980)
Full-information item bi-factor analysis
Robert D. Gibbons & Donald R. Hedeker
Psychometrika 57.3 (September 1992)
Sensitivity of MRQAP Tests to Collinearity and Autocorrelation Conditions
David Dekker, David Krackhardt & Tom A. B. Snijders
Psychometrika 72.4 (December 2007)
Test reliability estimated by analysis of variance
Cyril Hoyt
Psychometrika 6.3 (June 1941)
On the multivariate asymptotic distribution of sequential Chi-square statistics
James H. Steiger, Alexander Shapiro & Michael W. Browne
Psychometrika 50.3 (September 1985)
Contributions to factor analysis of dichotomous variables
Bengt Muthén
Psychometrika 43.3 (December 1978)
Representation of structure in similarity data: Problems and prospects
Roger N. Shepard
Psychometrika 39.4 (December 1974)
A nonparametric approach for assessing latent trait unidimensionality
William Stout
Psychometrika 52.4 (December 1987)
OpenMx 2.0: Extended Structural Equation and Statistical Modeling
Michael C. Neale, Michael D. Hunter, Joshua N. Pritikin, Mahsa Zahery, Timothy R. Brick, Robert M. Kirkpatrick, Ryne Estabrook, Timothy C. Bates, Hermine H. Maes & Steven M. Boker
Psychometrika 81.2 (June 2016)
A least squares algorithm for fitting additive trees to proximity data
Geert De Soete
Psychometrika 48.4 (December 1983)
Alpha factor analysis
Henry F. Kaiser & John Caffrey
Psychometrika 30.1 (March 1965)
EM algorithms for ML factor analysis
Donald B. Rubin & Dorothy T. Thayer
Psychometrika 47.1 (March 1982)
Power of the likelihood ratio test in covariance structure analysis
Albert Satorra & Willem E. Saris
Psychometrika 50.1 (March 1985)
A dynamic factor model for the analysis of multivariate time series
Peter C. M. Molenaar
Psychometrika 50.2 (June 1985)
Orthogonal rotation to congruence
Norman Cliff
Psychometrika 31.1 (March 1966)
线性代数不是我业余研究专业里的东西。它和我工作的专业倒是有些联系,不过在那儿我也就是个硕士水平。
没有光子;也没有量子能级,量子跃迁,量子叠加,量子塌缩和量子纠缠。
Re: (大妈出蹄)图形学:矩阵的第二个特征向量为何能用来分类
你还没有发现么?我发言,只在有点自己的想法想要表达的时候。回答一个常规问题,不在这个范围之内。也就看看。
没想法就不发言,希望更多人这样。
没想法就不发言,希望更多人这样。

