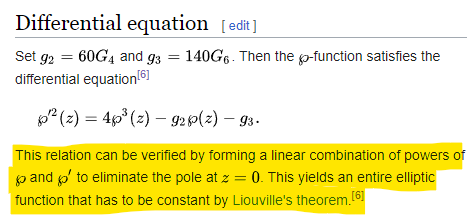新未名空间

FoxMe 写了： 2023年 9月 7日 09:20 "上半复平面quotient by modular group给出了所有椭圆曲线, up to isomorphism."

上半复平面quotient by modular group，也有一个专门名词，叫modular curve，这是moduli space的一个例子。

但是modular curve为啥也是曲线（有时是椭圆曲线），实在令人费解。

这个quotient space，Γ\H，局部也是复平面，实二维。我觉得代数几何里是不是把这种点集都叫做“曲线”了？modular curve好像并不是一个方程给出的点集。我看到有modular equation的说法，但是好像并不是解集的关系。

FoxMe 写了： 2023年 9月 7日 09:23 有人把{az+b, cz+d}到{(az+b)/(cz+d), 1}解释为projective，这和椭圆曲线是projective curve有啥关系吗？

这个我觉得就是一个旋转和缩放。格点的旋转和缩放对形成的椭圆函数应该是一个线性的影响，得到的椭圆曲线也是同构的。

另外，椭圆曲线的同构，不仅指拓扑同构，还要求代数上的同构吧？比如点作为群元素的order。

椭圆曲线的同构，可以定义为群同构。

FoxMe 写了： 2023年 9月 7日 16:44 椭圆曲线的同构，可以定义为群同构。

嗯对。群同构已经包含了拓扑同构 - 在复变的情况下 - 应该是各种情况下。

都是高手，学过Abelian簇，还学过算术几何。

FoxMe 写了： 2023年 9月 1日 18:14 假如P(u)和P(v)来参数化两点U和V，第三点W=U+V的参数恰好是P(u+v)。

这个有reference吗？wiki上有吗？

假设
U = (x,y) = (P(u),P'(u))
V = (x,y) = (P(v),P'(v))
W = (x,y) = (P(u+v),P'(u+v))
这里P是Weierstrass P函数，根据P函数的性质
P'² = 4P³-g₂P-g₃
那么U,V,W自动在椭圆曲线
y²=4x³-g₂x-g₃
上。

要证明U,V,W满足椭圆曲线上的群加法W=U+V，只需证明U,V,W三点共线。

要用到P(u+v)这个公式（不知道怎么推出来的）

https://en.wikipedia.org/wiki/Weierstra ... n_theorems

刚好和用几何作图得到的第三个点W的坐标相同

https://en.wikipedia.org/wiki/Elliptic_ ... rpretation

FoxMe 写了： 2023年 9月 8日 17:33 要用到P(u+v)这个公式（不知道怎么推出来的）

https://en.wikipedia.org/wiki/Weierstra ... n_theorems

刚好和用几何作图得到的第三个点W的坐标相同

https://en.wikipedia.org/wiki/Elliptic_ ... rpretation

不错。这个P函数加法公式的确可以推出椭圆曲线上的三点共线。

这个P函数的加法公式，应该还是着落在P函数的级数表达上。

TheMatrix 写了： 2023年 9月 8日 19:34 不错。这个P函数加法公式的确可以推出椭圆曲线上的三点共线。

这个P函数的加法公式，应该还是着落在P函数的级数表达上。

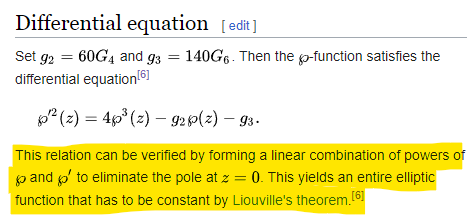
这个小东西我本来以为可以通过对级数项的tracking得到，但是得不出来。找到了一个证明。再一看，wiki上也是这么写的。看来不是tracking排列组合能得到的，必须通过复变函数的性质。

当年的人把复变函数的性质玩透了。我记得我高中的时候，圆锥曲线求交点，不用算，一看就知道结果 - 忘了是不是这么个问题了，总之就是当年玩得太熟了。

FoxMe 写了： 2023年 9月 3日 11:00 代数几何与数论结合起来，就更有意思了，叫算术几何。数论中的很多问题，比如多项式方程的有理解，需要算术几何。

比如椭圆曲线上的有理点组成一个群，叫Mordell-Weil群。Mordell-Weil定理说这个群是有限生成的，那么它的秩是多少？现在还没有解决，只有一个猜想：BSD猜想，它说Mordell-Weil群的秩等于椭圆曲线的L函数在s=1处的零点的阶。典型的解析数论。

BSD猜想是七个千禧数学猜想之一。中国人应该往这个方向努力，争取证明它。BSD猜想应该是最有可能下一个被证明的千禧猜想，以为费马大定理的这么已经做了很多铺垫，比如椭圆曲线与modular form的联系。

While BSD conjecture gives a very accurate relation between certain important quantities related to an elliptic curve, the most important information it contains is probably what you mentioned, rank of the Mordell-Weil group of E (the so-called algebraic rank) = order of vanishing of the L(s, E) at s=1 (analytic rank). Even though this not fully solved yet, we have known that the two ranks are equal when the analytic rank is 0 or 1. This is already very useful. While it is believed that the rank of E/Q can be arbitrarily large, it is also conjectured that, if all elliptic curves over Q are categorized in a reasonable way, then (asymptotically) half of them have rank 0 and half of them have rank 1. In particular, Goldfeld (in 1979?) had such a conjecture for the quadratic twists of any given E/Q. A folklore "Density Conjecture" followed from Goldfeld's conjecture states that, for any give E/Q, a positive proportion of the quadratic twists of E/Q have rank 0, and another positive proportion have rank 1. So if you can show that a positive proportion of the quadratic twists have ANALYTIC rank 0 (or 1), then you have the Density Conjecture for the curve. In late 1990's, Ono and Skinner, James, and another Indian guy (I forgot the name) adopted this approach.

san721 写了： 2023年 9月 13日 10:14 While BSD conjecture gives a very accurate relation between certain important quantities related to an elliptic curve, the most important information it contains is probably what you mentioned, rank of the Mordell-Weil group of E (the so-called algebraic rank) = order of vanishing of the L(s, E) at s=1 (analytic rank). Even though this not fully solved yet, we have known that the two ranks are equal when the analytic rank is 0 or 1. This is already very useful. While it is believed that the rank of E/Q can be arbitrarily large, it is also conjectured that, if all elliptic curves over Q are categorized in a reasonable way, then (asymptotically) half of them have rank 0 and half of them have rank 1. In particular, Goldfeld (in 1979?) had such a conjecture for the quadratic twists of any given E/Q. A folklore "Density Conjecture" followed from Goldfeld's conjecture states that, for any give E/Q, a positive proportion of the quadratic twists of E/Q have rank 0, and another positive proportion have rank 1. So if you can show that a positive proportion of the quadratic twists have ANALYTIC rank 0 (or 1), then you have the Density Conjecture for the curve. In late 1990's, Ono and Skinner, James, and another Indian guy (I forgot the name) adopted this approach.

L(s, E) at s=1 是 zero 还是 pole？

TheMatrix 写了： 2023年 9月 13日 12:57 L(s, E) at s=1 是 zero 还是 pole？

Zero. For an elliptic curve E/Q, its L-function is an entire function and thus has no poles.

san721 写了： 2023年 9月 13日 13:21 Zero. For an elliptic curve E/Q, its L-function is an entire function and thus has no poles.

嗯。L-function只有在特殊情况下，在s=1点才是pole，不是pole的情况应该是大多数情况。

FoxMe 写了： 2023年 9月 3日 11:00 代数几何与数论结合起来，就更有意思了，叫算术几何。数论中的很多问题，比如多项式方程的有理解，需要算术几何。

比如椭圆曲线上的有理点组成一个群，叫Mordell-Weil群。Mordell-Weil定理说这个群是有限生成的，那么它的秩是多少？现在还没有解决，只有一个猜想：BSD猜想，它说Mordell-Weil群的秩等于椭圆曲线的L函数在s=1处的零点的阶。典型的解析数论。

BSD猜想是七个千禧数学猜想之一。中国人应该往这个方向努力，争取证明它。BSD猜想应该是最有可能下一个被证明的千禧猜想，以为费马大定理的这么已经做了很多铺垫，比如椭圆曲线与modular form的联系。

这个L-function确实很厉害。相当于把椭圆曲线的信息组织到了一起，而组织的是否恰当，就看这个函数有没有什么优美的特征。BSD猜想就说明它的确有很优美的特征。

不知道wiki上这句话具体是什么意思。

通过P(z)级数展开也行，得到P^3(z)和P'(Z)的级数后，截止到常数项进行比较。因为包含z, z^2, ...的项是一个完纯函数，所以根据刘维尔定理等于0.

复变函数是门学问，对于解析数论非常有用。但是一般都没教椭圆函数，伽马函数等数论中常用的函数。

圆锥曲线是我中学的噩梦，不知道当时为啥不懂。

TheMatrix 写了： 2023年 9月 9日 21:12

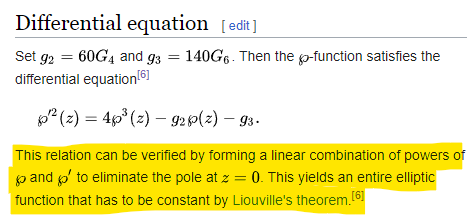
这个小东西我本来以为可以通过对级数项的tracking得到，但是得不出来。找到了一个证明。再一看，wiki上也是这么写的。看来不是tracking排列组合能得到的，必须通过复变函数的性质。

当年的人把复变函数的性质玩透了。我记得我高中的时候，圆锥曲线求交点，不用算，一看就知道结果 - 忘了是不是这么个问题了，总之就是当年玩得太熟了。

再往前一步，就是Langlands program。

TheMatrix 写了： 2023年 9月 13日 16:17 这个L-function确实很厉害。相当于把椭圆曲线的信息组织到了一起，而组织的是否恰当，就看这个函数有没有什么优美的特征。BSD猜想就说明它的确有很优美的特征。

FoxMe 写了： 2023年 9月 16日 17:24 再往前一步，就是Langlands program。

你能不能介绍一下Langlands program?

我不是专家，我的感觉是Langlands program就是现代的解析数论。陈锦润时代的解析数论，学了初等数论和复变函数，就可以开始研究了。研究Langlands program，要把纯数学方向的全部课都学了才行。

BSD猜想的研究对象是有理数域Q上的椭圆曲线。这里的L函数已经非常厉害了，除了BSD，还有费马大定理的证明用到：Q上的椭圆曲线的L函数对应于一个modular form。这个对应关系是不可思议的，因为一边是数论，一边是复变函数。

那么至少有两个方向可以推广：从有理数域Q到代数数域，从椭圆曲线到代数簇，它们的L函数也（猜想）对应于类似于modular form，叫automorphic form。这些猜想大部分都还没有被证明。

总之，Langlands program相当于一座桥梁，把数学的各个分支（数论，代数，几何，分析）联系起来了。相当于数学中的统一场论。

FoxMe 写了： 2023年 9月 18日 13:46 我不是专家，我的感觉是Langlands program就是现代的解析数论。陈锦润时代的解析数论，学了初等数论和复变函数，就可以开始研究了。研究Langlands program，要把纯数学方向的全部课都学了才行。

BSD猜想的研究对象是有理数域Q上的椭圆曲线。这里的L函数已经非常厉害了，除了BSD，还有费马大定理的证明用到：Q上的椭圆曲线的L函数对应于一个modular form。这个对应关系是不可思议的，因为一边是数论，一边是复变函数。

那么至少有两个方向可以推广：从有理数域Q到代数数域，从椭圆曲线到代数簇，它们的L函数也（猜想）对应于类似于modular form，叫automorphic form。这些猜想大部分都还没有被证明。

总之，Langlands program相当于一座桥梁，把数学的各个分支（数论，代数，几何，分析）联系起来了。相当于数学中的统一场论。

这里确实很丰富，互相之间的关系太多了。好多关系我没搞清楚：
椭圆曲线
椭圆函数
modular form
modular function
modular group
modular curve
L-function
Galois representation

我也是在学。L函数是关键，有很多种。比如伽罗瓦数域的L函数怎么定义？

https://en.wikipedia.org/wiki/Artin_L-f ... Definition

如果伽罗瓦群可换，那么伽罗瓦群有一维表示，乘起来就行了；
如果伽罗瓦群不可换，那么就要用到伽罗瓦群的表示理论。