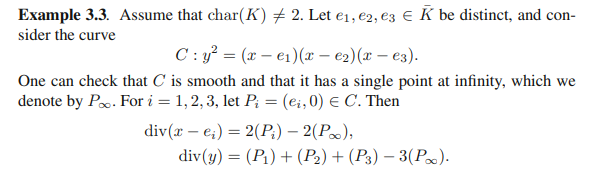关于椭圆曲线，听说这本书不错

[TheMatrix]

第三章我还没看，打算快速过一遍全书，再来看第三章。这本书起点太高，直接从代数几何开始。

这个是第二章的，Example 3.3。完整编号是II.3.3。

[san721]

http://www.pdmi.ras.ru/~lowdimma/BSD/Si ... _of_EC.pdf

GTM 106，
Silverman, The Arithmetic of Elliptic Curves.
Springer, 2nd edition, 2009.

就算是数学专业的，如果没有代数和几何基础，我觉得Silverman这本书太难了。有一本Tate和Silverman的书

https://www.amazon.com/Rational-Points- ... 0387978259

作为elliptic curve入门书很不错的。虽说这是本UTM, 其实真要作为本科教材，恐怕也只适合最top的数学专业undergraduate students。

[san721]

"A supersingular elliptic curve is, by definition, an elliptic curve, so it is nonsingular."这个定义坑人啊。

我手边现在没有这本书，但我猜测这是在谈论supersingular reduction。“so it is nonsingular” 意思是说作为一条椭圆曲线，首先globally它是non-singular的。对于一个素数p, 一条椭圆曲线E/Q 的mod p reduction是supersingular的if |E(F_p)|=p+1或者说，这条曲线的L-function对应的系数a_p=0. Noam Elkies在1987年证明了，对于任何一条给定的E/Q, it has infinitely many supersingular primes.

[TheMatrix]

就算是数学专业的，如果没有代数和几何基础，我觉得Silverman这本书太难了。有一本Tate和Silverman的书

https://www.amazon.com/Rational-Points- ... 0387978259

作为elliptic curve入门书很不错的。虽说这是本UTM, 其实真要作为本科教材，恐怕也只适合最top的数学专业undergraduate students。

谢谢。

这个网上有：http://ndl.ethernet.edu.et/bitstream/12 ... verman.pdf

我看到math exchange有问答说了Silverman的三件套：这个是第一本，然后是我主贴里的那本，最后还有一个advance topic。

我现在看的这本书确实挺难的。我再看看。我会用这本UTM的做参考。

[TheMatrix]

Coordinate ring, local ring, Ord_P of a function in the function field of a curve, 把我整糊涂了。我先休息一下，这个先留在这。

这个我把数字具体下来，画了个图：



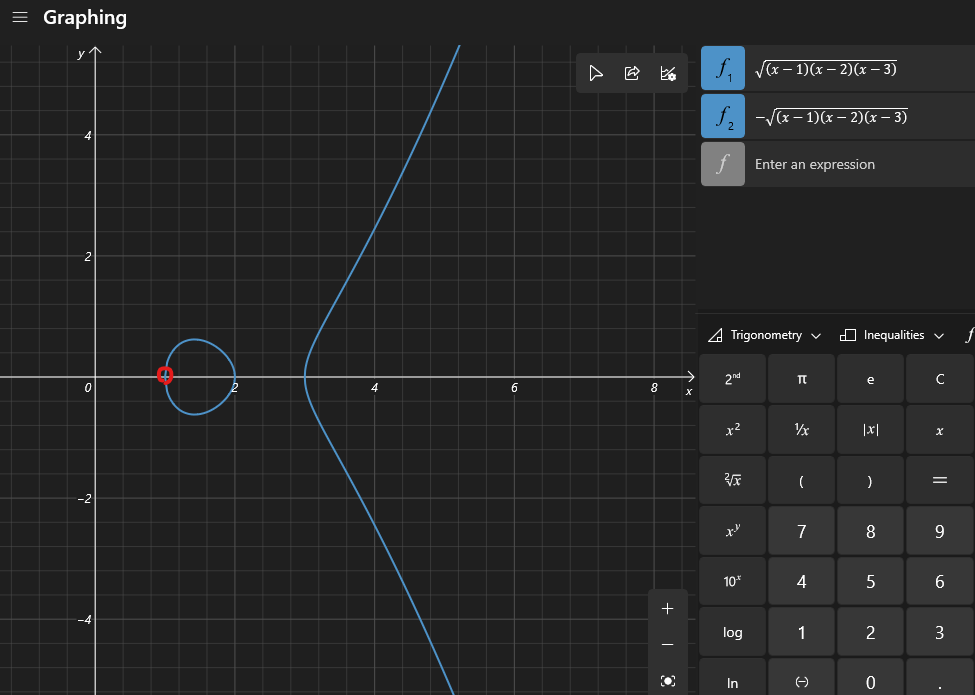
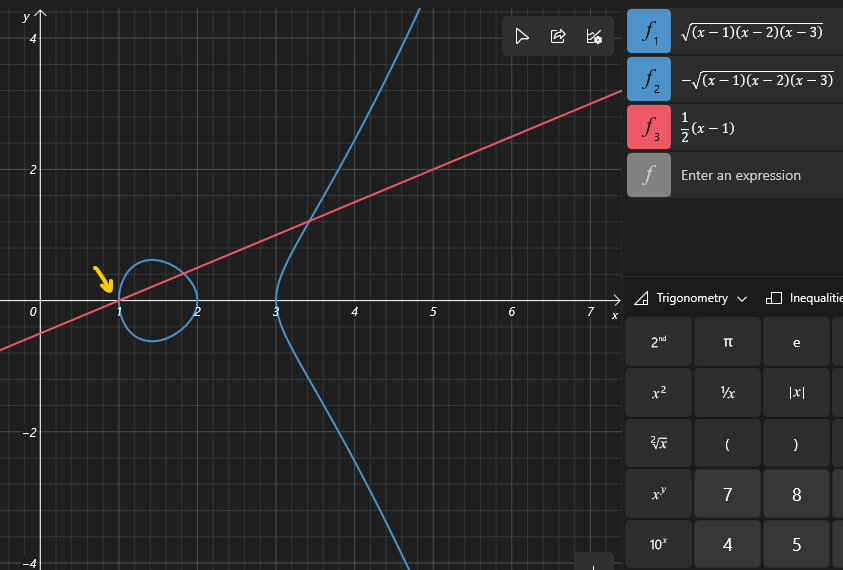
这里e₁=1，P₁=(1,0)。

按照divisor的定义，这个例子就是说，x-1这个polynomial，作为椭圆曲线C上一个函数，它在P₁点的order是2。这个order，我理解它就是几阶零点的意思。x-1在P₁点是2阶零点，不是1阶，是2阶。这个地方肯定因为它考虑的是在C上，不是一个裸的。

几何上好像是可以理解的，因为x=1在P₁点是切线嘛。但是我想用它的定义来理解一下。它是用P₁点local ring的ideal M_P来定义的。这个地方理解一下还是有好处的。我还没理解出来。

[TheMatrix]

而红色这条直线，是x-2y-1这个polynomial，x-2y-1=0，y=1/2(x-1)，它在(1,0)点和椭圆曲线斜交，所以它的order为1。这应该就是它的几何意义。

[TheMatrix]

这个我把数字具体下来，画了个图：



这里e₁=1，P₁=(1,0)。

按照divisor的定义，这个例子就是说，x-1这个polynomial，作为椭圆曲线C上一个函数，它在P₁点的order是2。这个order，我理解它就是几阶零点的意思。x-1在P₁点是2阶零点，不是1阶，是2阶。这个地方肯定因为它考虑的是在C上，不是一个裸的。

几何上好像是可以理解的，因为x=1在P₁点是切线嘛。但是我想用它的定义来理解一下。它是用P₁点local ring的ideal M_P来定义的。这个地方理解一下还是有好处的。我还没理解出来。

这个差不多清楚了：P₁=(1,0) 本身的prime ideal是(x-1,y)，因为 x-1=0,y=0 决定了这个点。这也是一个K[x,y]的maximal ideal。

再考虑该点在椭圆曲线上的话，同时还要满足椭圆曲线的方程，也就是 y²=(x-1)(x-2)(x-3)。那么 x-1这个polynomial，作为椭圆曲线上的函数的话，也就是要modulo 椭圆曲线方程，（意思就是 x-1 和 (x-1) + f(x)[y²-(x-1)(x-2)(x-3)] 在椭圆曲线上是一样的），也就是x-1=y²/((x-2)(x-3))。

这个作为椭圆曲线P₁点local ring（可以有分母）的一个元素的话，它是属于M_P² ideal的，（M_P是local ring上的唯一ideal，也是从前面那个maximal ideal (x-1,y) 过来的），因为它分子上是个y²嘛。

从零点的阶数上看，它也是二阶的，还是因为分子上的y²。

[TheMatrix]

这个差不多清楚了：P₁=(1,0) 本身的prime ideal是(x-1,y)，因为 x-1=0,y=0 决定了这个点。这也是一个K[x,y]的maximal ideal。

再考虑该点在椭圆曲线上的话，同时还要满足椭圆曲线的方程，也就是 y²=(x-1)(x-2)(x-3)。那么 x-1这个polynomial，作为椭圆曲线上的函数的话，也就是要modulo 椭圆曲线方程，（意思就是 x-1 和 (x-1) + f(x)[y²-(x-1)(x-2)(x-3)] 在椭圆曲线上是一样的），也就是x-1=y²/((x-2)(x-3))。

这个作为椭圆曲线P₁点local ring（可以有分母）的一个元素的话，它是属于M_P² ideal的，（M_P是local ring上的唯一ideal，也是从前面那个maximal ideal (x-1,y) 过来的），因为它分子上是个y²嘛。

从零点的阶数上看，它也是二阶的，还是因为分子上的y²。

然后还要说明x-1这个多项式，作为椭圆曲线上的函数，在P_∞点有一个2阶pole。也就是ord_P∞=-2。这个应该用projective coordinate。这个我一直也没有完全搞清楚。花点时间搞清楚还是有好处的。

projective coordinate的起源实际上是很简单的，它的演算规则也是很机械化，而且从起源演变也是很自然的。

[FoxMe]

这么一说是很有道理，但是M_P, M^2_P这里我还没有完全搞懂，还在看。

[TheMatrix]

这个我把数字具体下来，画了个图：



这里e₁=1，P₁=(1,0)。

按照divisor的定义，这个例子就是说，x-1这个polynomial，作为椭圆曲线C上一个函数，它在P₁点的order是2。这个order，我理解它就是几阶零点的意思。x-1在P₁点是2阶零点，不是1阶，是2阶。这个地方肯定因为它考虑的是在C上，不是一个裸的。

几何上好像是可以理解的，因为x=1在P₁点是切线嘛。但是我想用它的定义来理解一下。它是用P₁点local ring的ideal M_P来定义的。这个地方理解一下还是有好处的。我还没理解出来。

分析上看，x-1是一个函数，看成(x,y)二维函数。x-1沿着椭圆曲线走得到一个椭圆曲线上的函数f，可以说是一个一维上的函数。这个函数f它也有零点，也就是x-1=0这条直线和椭圆曲线的交点P。f在P点的零点是几阶？问的就是这个问题。

分析上还需要仔细定义 - f以什么方式接近于P点，是沿着曲线弧线接近还是其他方式？代数几何中应该都是一样的，因为只研究多项式，而且只研究零点的阶，也就是比如λx以线性的方式接近于0，那就是1阶，λx²以2次方的形式接近于0，那就是2阶。分析还可以研究的更细，线性的系数是什么，二次方的系数是什么，都可以研究。

[FoxMe]

看了一下，基本搞懂了。div(f)基本上就是零极点的一种形式化表示。

x-1=y^2/((x-2)(x-3)), 在y=0处是2阶零点，在y=∞处是2阶极点。

y=((x-1)(x-2)(x-3))/y, 在x=1,2,3处是1阶零点，在x=∞处是3阶极点。

但这种说法这是不严格的，严格的还要用M_P.

P_∞该怎么定义？齐次化得Y²Z=(X-Z)(X-2Z)(X-3Z),一般用[X:Y:Z]=[0:1:0]表示P_∞，但是不知道怎么对上。

然后还要说明x-1这个多项式，作为椭圆曲线上的函数，在P_∞点有一个2阶pole。也就是ord_P∞=-2。这个应该用projective coordinate。这个我一直也没有完全搞清楚。花点时间搞清楚还是有好处的。

projective coordinate的起源实际上是很简单的，它的演算规则也是很机械化，而且从起源演变也是很自然的。

[TheMatrix]

看了一下，基本搞懂了。div(f)基本上就是零极点的一种形式化表示。

x-1=y^2/((x-2)(x-3)), 在y=0处是2阶零点，在y=∞处是2阶极点。

y=((x-1)(x-2)(x-3))/y, 在x=1,2,3处是1阶零点，在x=∞处是3阶极点。

但这种说法这是不严格的，严格的还要用M_P.

P_∞该怎么定义？齐次化得Y²Z=(X-Z)(X-2Z)(X-3Z),一般用[X:Y:Z]=[0:1:0]表示P_∞，但是不知道怎么对上。

对，函数的divisor就是把它的零点和极点带着order表出。但是x-1在P_∞是二阶极点，这个怎么说明，还没有完全清楚。x-1=y^2/((x-2)(x-3))，好像不能光看分子上有一个y²，因为分母上的(x-2)和(x-3)在P_∞都不是bounded的。如果说y本身在P_∞是3阶极点，那么y²就是6阶极点，然后每一个(x-1)，(x-2)，(x-3)，都是2阶极点，这倒是对上了。但是这个可能循环了。

是。我也在想怎么用齐次化来说明这个问题。Y²Z=(X-Z)(X-2Z)(X-3Z)，在P_∞=[0:1:0]点。

[TheMatrix]

Coordinate ring, local ring, Ord_P of a function in the function field of a curve, 把我整糊涂了。我先休息一下，这个先留在这。

这个问题部分想通了，还剩下一些。我也没有死磕 - 磕了不到一天 - 把第二章剩下的读完了。不过这个问题以后也是需要继续想清楚的。

主要关注的是定义、定理的叙述，和例子。大部分证明都略过了。很多东西我还没有感性认识，比如Riemann-Roch定理，名字知道，以前看过，当时是对大脑的摩擦，现在还是。

接下来看第三章了，正式进入主题。从标题看，感觉是对感性认识的抽象提高，看来需要参考UTM那本啊。

[FoxMe]

Riemann-Roch定理是核心的，可以用来构造代数几何码，也是一门显学。

但是有很多地方看不懂，比如differential的概念：

Definition. Let C be a curve. The space of (meromorphic) differential forms on C, denoted by ΩC, is the K ̄-vector space generated by symbols of the form dx for x ∈ K ̄ (C ), subject to the usual relations:
(i) d(x+y)=dx+dy forallx,y∈K ̄(C).
(ii) d(xy)=xdy+ydx forallx,y∈K ̄(C).
(iii) da=0 foralla∈K ̄.

这里dx看上去就是微分，怎么会出现一个矢量空间？没给例子，不知所云。

[FoxMe]

https://www.win.tue.nl/~aeb/2WF02/rr.pdf

8 Algebraic Geometry Codes

Pick a divisor D, say with 2g−1 < degD < n, and let P1, ..., Pn be points outside the support of D.

Make a code C = {(f(P1), ..., f(Pn)) | f ∈ L(D)}.

Theorem 8.1 The code C has word length n, dimension k = l(D) = deg(D) +1 − g and minimum distance d ≥ n − deg(D).

Proof That C has word length n is clear. The statement about the dimension was a corollory above. If C has minimum distance d, then there is a function f such that f ∈ L(D′) where D′ = D − 􏰅f(Pi)=0 Pi, with deg(D′) = deg(D) − (n − d) ≥ 0.

代数几何码的构造和证明极其简单。为啥there is a function f such that f ∈ L(D′)？

[TheMatrix]

Riemann-Roch定理是核心的，可以用来构造代数几何码，也是一门显学。

Riemann-Roch太抽象，heavy machinery，就是为了得到一个genus，我现在还领略不了。没有genus我也可以研究椭圆曲线啊 - 我查了UTM那本书，整本书没讲Riemann-Roch。

我看了UTM那本书，看了第一章和Appendix讲projective的。确实好读多了。

projective这段，我主要想看怎么在无穷远点求导。但是没找到intrinsic projective的方法。它的方法是：把projective space以另一个数轴做dehomogenize，那么无穷远点就变成了普通的一点，然后按照普通的求导来求。

我还在想y²=(x-1)(x-2)(x-3)，函数x-1在无穷远点是二阶极点的事。

[TheMatrix]

但是有很多地方看不懂，比如differential的概念：

Definition. Let C be a curve. The space of (meromorphic) differential forms on C, denoted by ΩC, is the K ̄-vector space generated by symbols of the form dx for x ∈ K ̄ (C ), subject to the usual relations:
(i) d(x+y)=dx+dy forallx,y∈K ̄(C).
(ii) d(xy)=xdy+ydx forallx,y∈K ̄(C).
(iii) da=0 foralla∈K ̄.

这里dx看上去就是微分，怎么会出现一个矢量空间？没给例子，不知所云。

我学过一些微分几何，differential的概念比较熟悉。

它这里是想做纯代数处理，所以说dx是一个symbol。对每一个函数x，（这里的x是任意函数，不是coordinate的那个x），都有一个dx symbol，然后做K ̄-vector space，这是free扩展。然后商去三个关系。第二个关系是微分关系。这里好像是有点问题：x能乘以dy，确实需要解释一下怎么乘。

[TheMatrix]

Riemann-Roch太抽象，heavy machinery，就是为了得到一个genus，我现在还领略不了。没有genus我也可以研究椭圆曲线啊 - 我查了UTM那本书，整本书没讲Riemann-Roch。

我看了UTM那本书，看了第一章和Appendix讲projective的。确实好读多了。

projective这段，我主要想看怎么在无穷远点求导。但是没找到intrinsic projective的方法。它的方法是：把projective space以另一个数轴做dehomogenize，那么无穷远点就变成了普通的一点，然后按照普通的求导来求。

我还在想y²=(x-1)(x-2)(x-3)，函数x-1在无穷远点是二阶极点的事。

在椭圆曲线y²=(x-1)(x-2)(x-3)上，函数x-1在无穷远点是二阶极点。

这里的问题是这么两点：

1，从分析的角度看，椭圆曲线（假设是over complex number）在P_∞附近complex拓扑同构于一个复平面（w变量），而x-1这个函数应该可以展开成1/w²+1/w+c₀+...的形式，所以是二阶极点。但是是以什么方式做的拓扑同构，这个没有说明。应该有一定的不变性，但还是有要求的。

2，从代数的角度看，就用书里的M_P的方式定义。但是它没讲M_P在P=P_∞的时候是怎么定义的。应该是要用到齐次多项式。

另外，这两个角度怎么调和，也是一个问题。

[FoxMe]

弄懂了，很简单： 因为P1, ..., Pn 和 support of D不相交. 把n-d个零点减掉对(f)+D≥0没有任何影响，所以f ∈ L(D′)。

据说代数几何码是史上最强的码，比5G编码还厉害，可是没人用，估计是复杂度太高。

https://www.win.tue.nl/~aeb/2WF02/rr.pdf

8 Algebraic Geometry Codes

Pick a divisor D, say with 2g−1 < degD < n, and let P1, ..., Pn be points outside the support of D.

Make a code C = {(f(P1), ..., f(Pn)) | f ∈ L(D)}.

Theorem 8.1 The code C has word length n, dimension k = l(D) = deg(D) +1 − g and minimum distance d ≥ n − deg(D).

Proof That C has word length n is clear. The statement about the dimension was a corollory above. If C has minimum distance d, then there is a function f such that f ∈ L(D′) where D′ = D − 􏰅f(Pi)=0 Pi, with deg(D′) = deg(D) − (n − d) ≥ 0.

代数几何码的构造和证明极其简单。为啥there is a function f such that f ∈ L(D′)？

[FoxMe]

放到代数几何码里，Riemann-Roch就变得具体了，这里一般假设genus已知。纯粹数学和应用结合是很好的。

我把divisor的概念弄懂了，但是怎么计算还是有问题。Differential则连概念还没弄懂 。

divisor group -> Picard group -> Jacobian variety -> Abelian variety，这是学习Abelian variety的一条路径。

Riemann-Roch太抽象，heavy machinery，就是为了得到一个genus，我现在还领略不了。没有genus我也可以研究椭圆曲线啊 - 我查了UTM那本书，整本书没讲Riemann-Roch。

我看了UTM那本书，看了第一章和Appendix讲projective的。确实好读多了。

projective这段，我主要想看怎么在无穷远点求导。但是没找到intrinsic projective的方法。它的方法是：把projective space以另一个数轴做dehomogenize，那么无穷远点就变成了普通的一点，然后按照普通的求导来求。

我还在想y²=(x-1)(x-2)(x-3)，函数x-1在无穷远点是二阶极点的事。