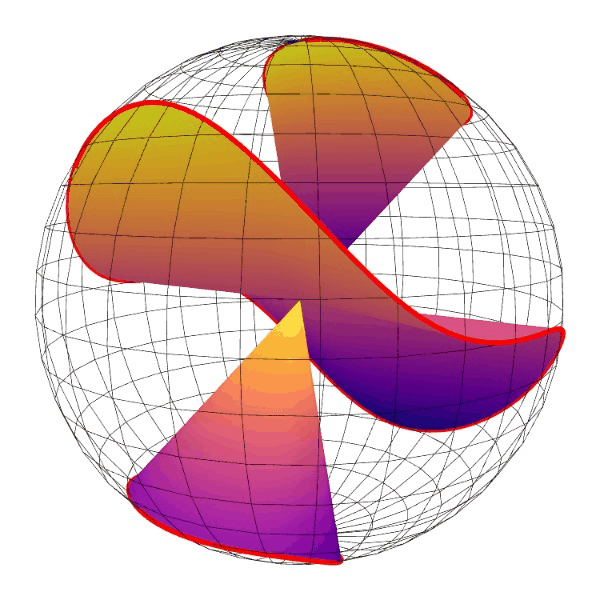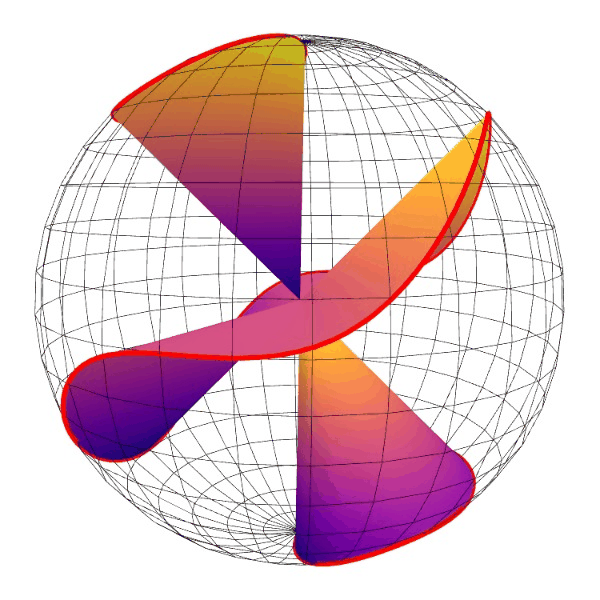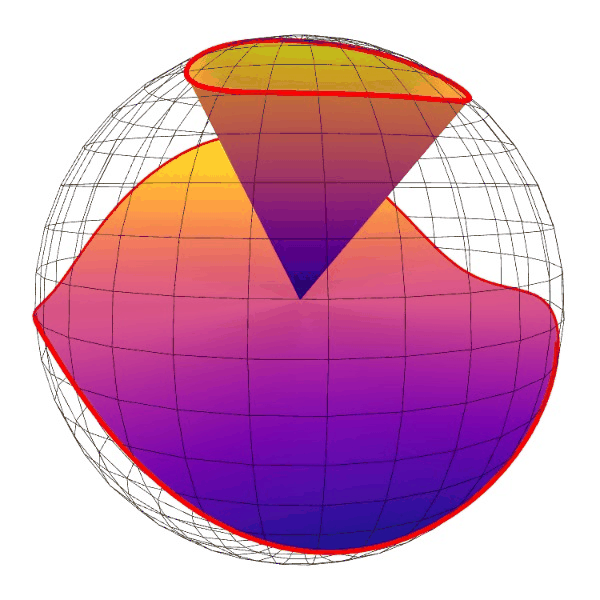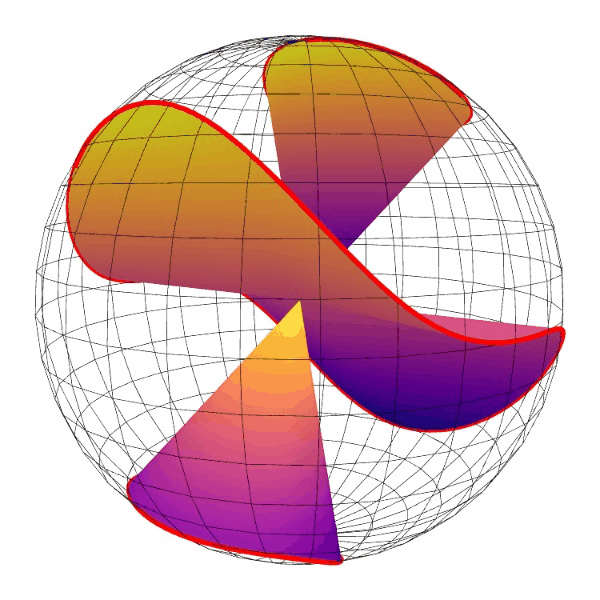
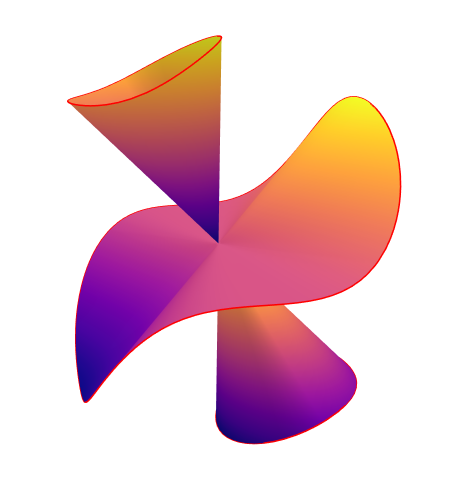外行瞎问一句,这个程序用gnuplot就是套用系统demo改改,为什么用py需要这么长时间?
贴个图
版主: verdelite, TheMatrix
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#22 Re: 贴个图
那主要是因为我不会用gnuplot。:)
不过我看了一下gnuplot。感觉和python matplotlib区别并不大。这个程序的难点主要有两个:
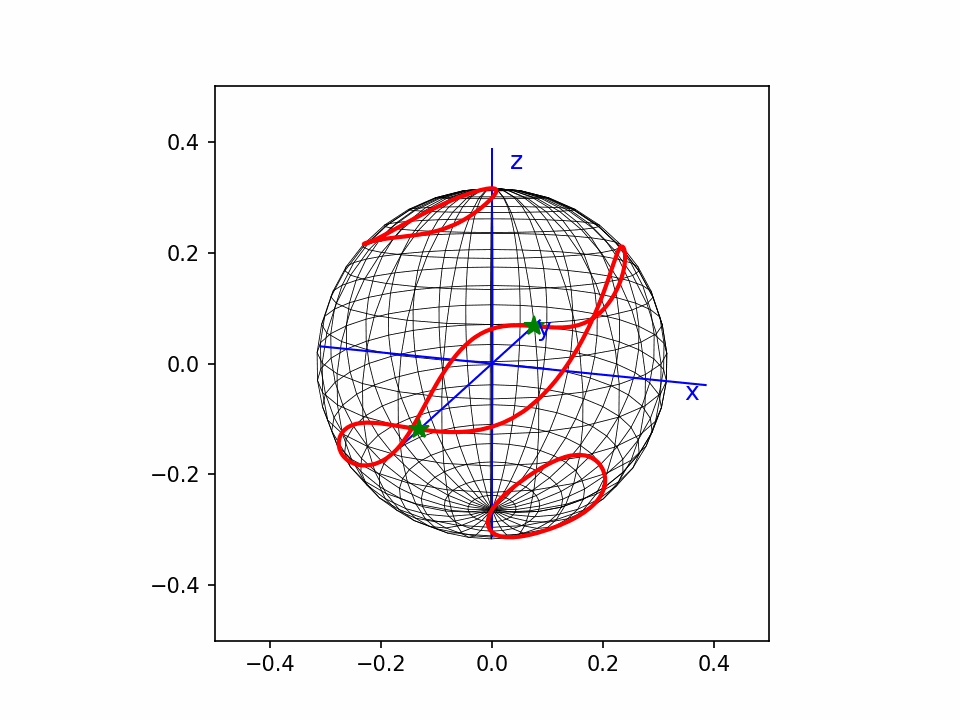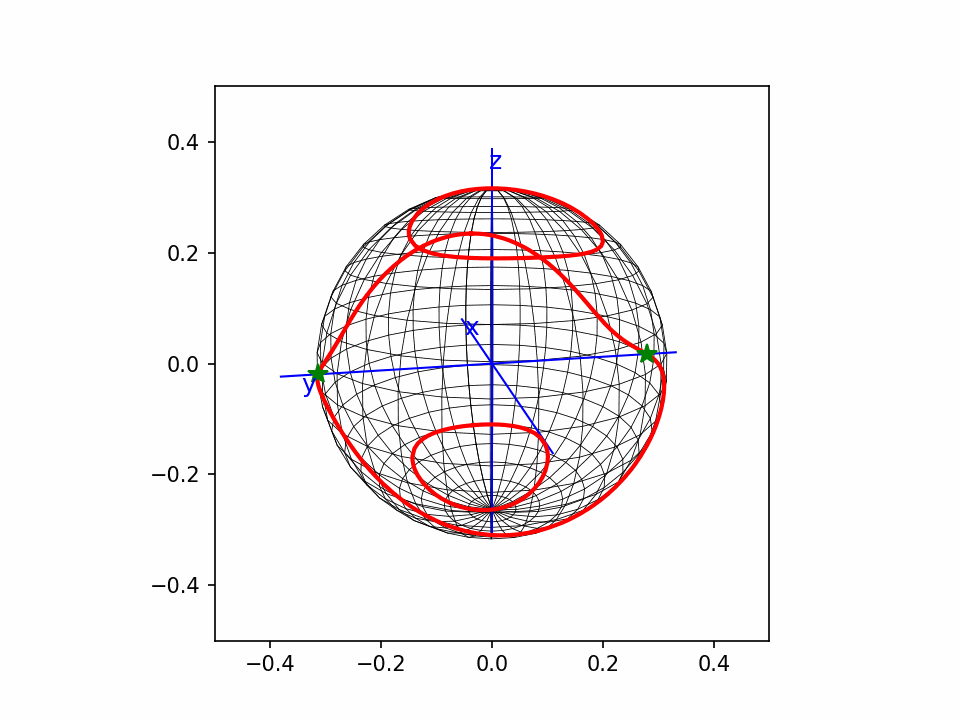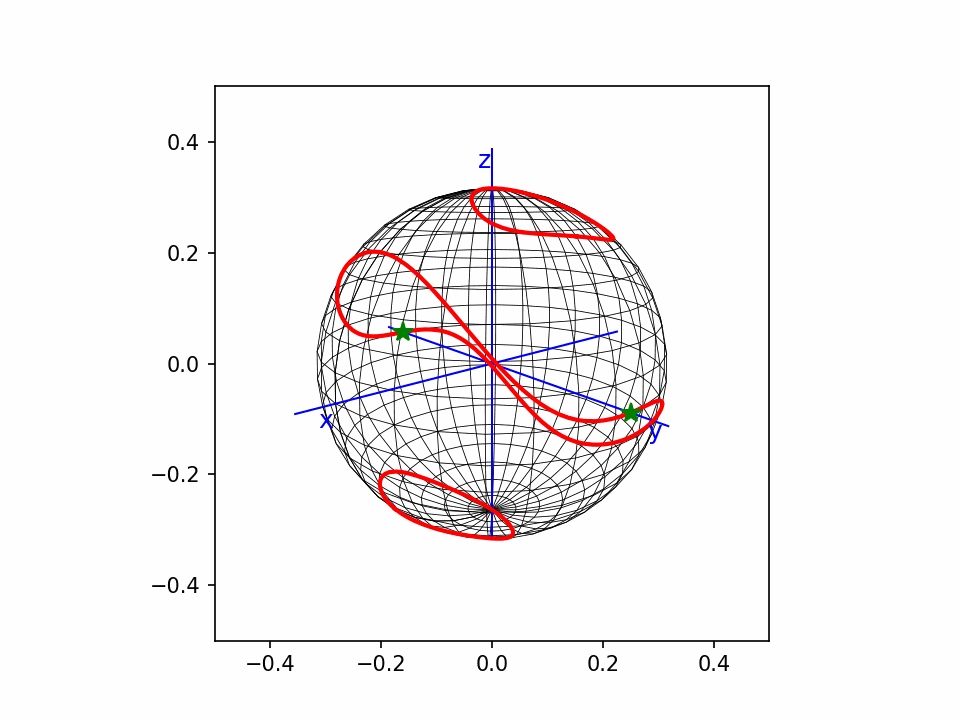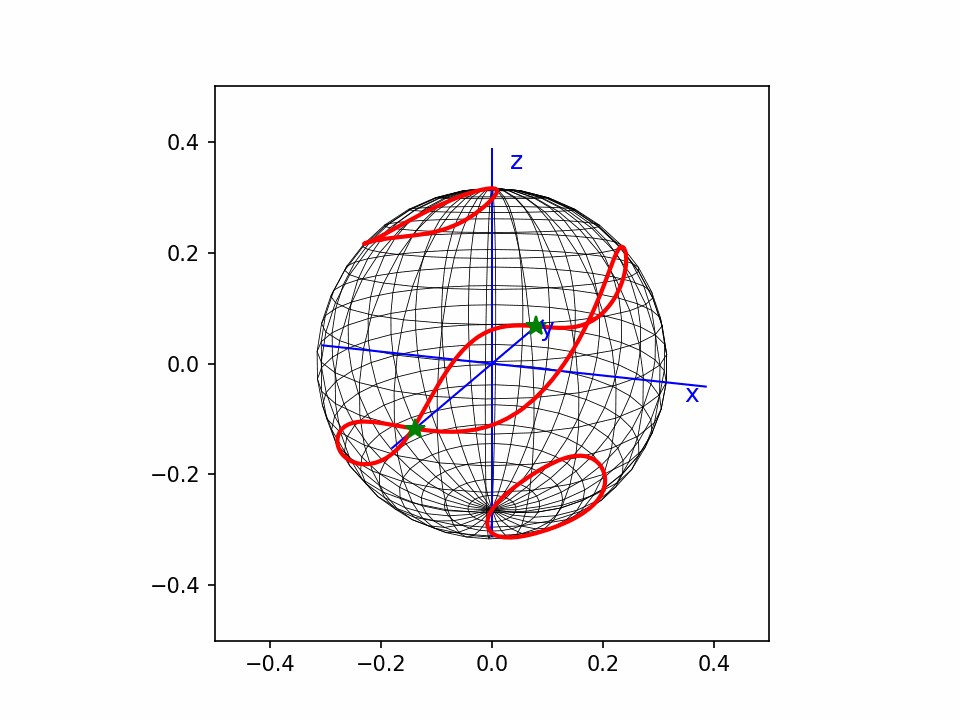
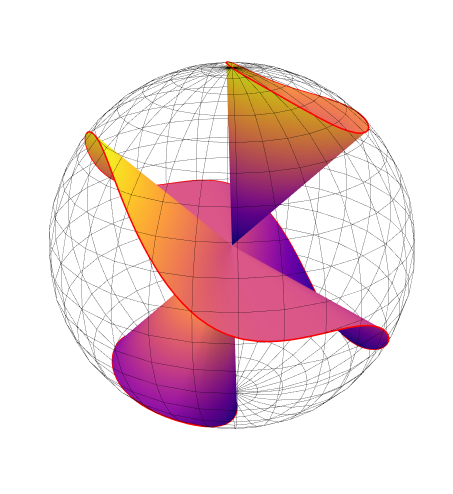
1,曲线的点分布。一般demo都是自变量均匀分布,而在曲线弧长上分布并不均匀,会造成某些地方的断续。我这个程序主要解决的就是这个问题。
2,遮挡,shading,光影。matplotlib画曲面只能通过transparency或者叫opaque来调整,gnuplot好像也差不多。曲线在球面上的这种问题,不能用这种方法解决。应该是用OpenGL shading的方法。
不过我主要是为了学习椭圆曲线。画图算是一个有趣的digression,可能不会花时间去学OpenGL。
#23 Re: 贴个图
明白了。怎么解释y=x3在无穷远点是cusp?我也记得,但是忘了为啥。
TheMatrix 写了: 2023年 11月 4日 21:54 又看了一下。这个和我画的是一样的。都是齐次方程在球面上的截取。因为球面是P2(R)的double cover,所以它也基本代表了齐次方程在P2(R)上的形象。
y=x3在球面上有cusp是对的。因为那个点正是无穷远点。y=x3在无穷远点是cusp。
#24 Re: 贴个图
直纹面能不能画出来?哈哈
TheMatrix 写了: 2023年 10月 29日 22:02 这是好问题啊。方程虽然和z无关,但是要研究方程在无穷远点的性质,也就是渐近线的性质,最方便的办法,就是把它齐次化。比如
y2=x3-x,
变成
y2z=x3-xz2
这样变了之后,如果(x,y,z)是解,那么λ(x,y,z)也是解,所以齐次方程的解是有直纹面构成的。
而如果用z=1平面截取这个齐次方程的解的话,得到的曲线就是原方程非齐次方程的解。
所以齐次化之后,信息不减少,只增多。增多的是什么呢?就是无穷远点的那一点:在齐次方程中,无穷远点由[0,1,0]这点所延申的直线代表 - 这条直线和z=1平面不相交的 - 可以认为相交于无穷远点。这些名词有点令人迷惑,但是在齐次方程中,这些词汇可以去掉。[0,1,0]所代表的直线,只是齐次方程直纹面解中的一个,和其他任何直线没有什么不同。也就是把“无穷远点”这种令人迷惑的概念化解了。
为什么要研究无穷远点?虽然只少了一点,但是在拓扑中,少了一大块。想想什么是无穷远点的邻域。这点的邻域去掉的话,还剩多少。这个地方是数学中的theme,有很深的理由,不容易说清楚。我先只能说这么多。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#27 Re: 贴个图
明白了。这么看,球面投影的意义就很明显了。终于体会到projective variety的好处了。
TheMatrix 写了: 2023年 11月 5日 09:38 这么看:
先齐次化:yz2=x3。
然后set y=1,相当于转个方向看这个曲线:z2=x3。
它在(x,z)=(0,0)点是一个cusp。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#28 Re: 贴个图
研究了一下。我这个点线3D图,叫wireframe。这种图静态没法看,因为后面本应被遮挡的线也能看见。动起来还是能看,但是也比较乱。
有遮挡的3D图,应该叫surface。每一块表面,可以叫face,或者叫patch,名字也是很合理的。前面的patch可以遮挡后面的patch,这个概念是很自然的。视觉效果就好多了。
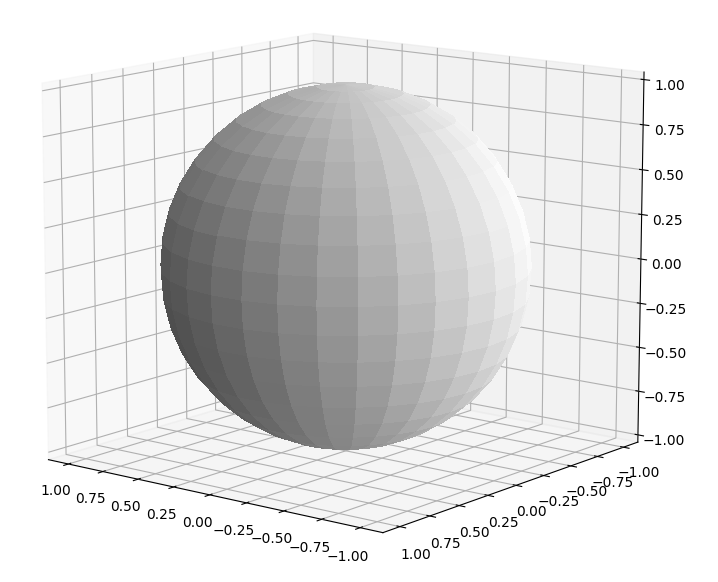
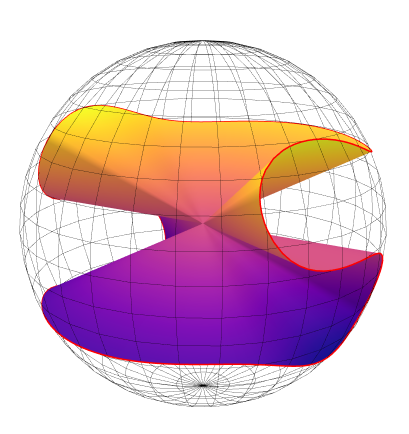
gnuplot 有遮挡效果的 surface:
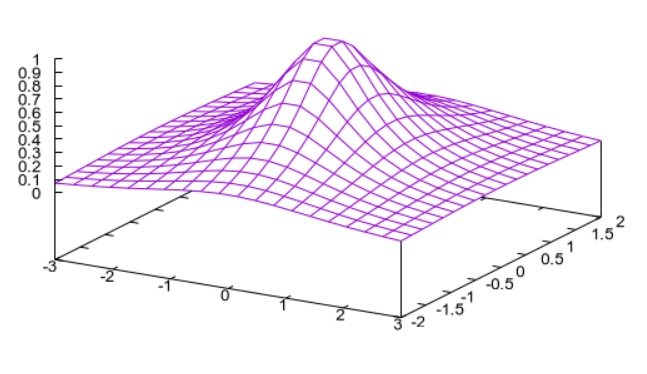
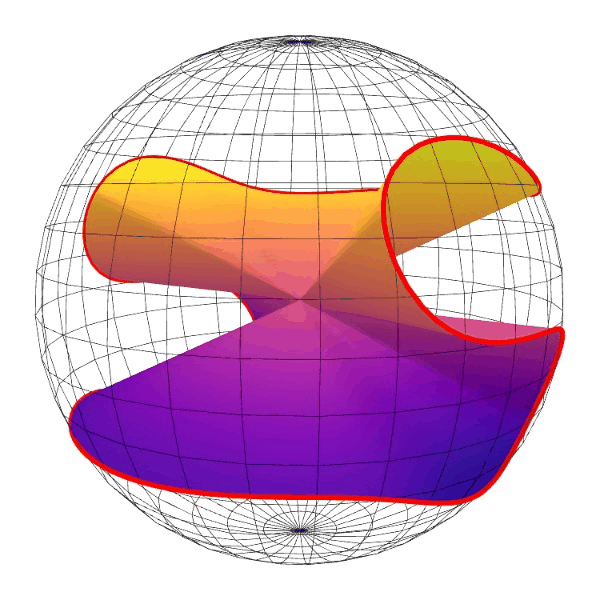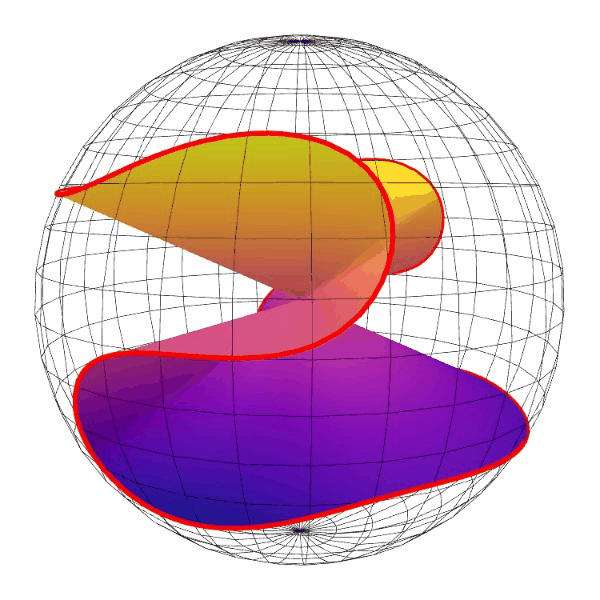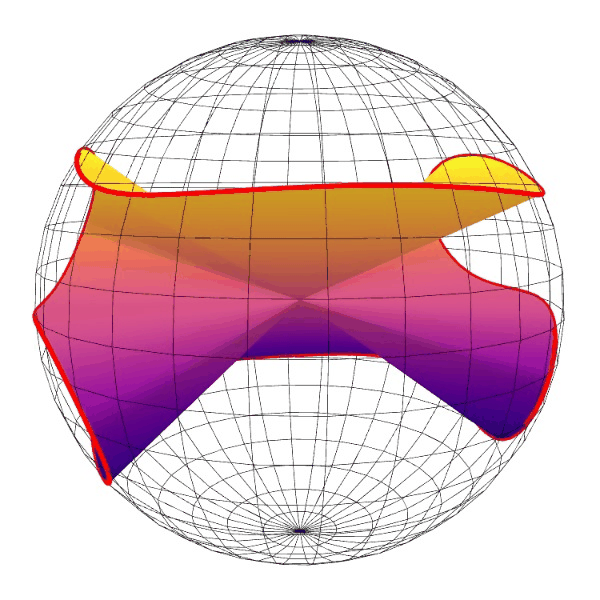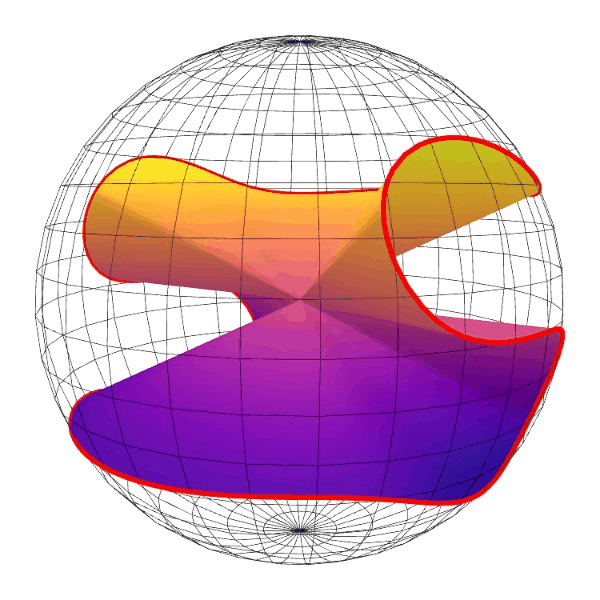
python matplotlib surface:
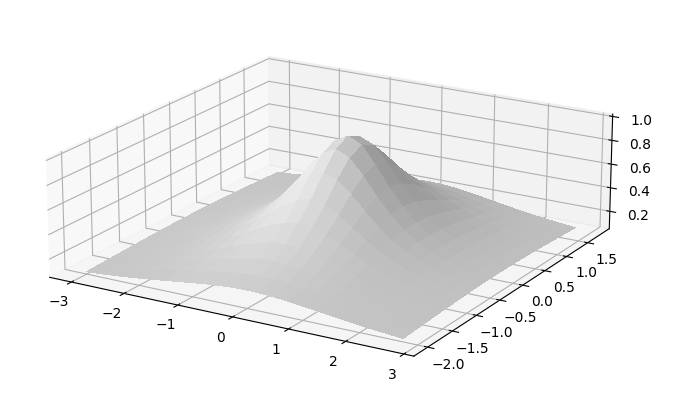
还是gnuplot的surface看着清楚。matplotlib的surface,调了一下颜色,线宽,color map,还是乱。不过它能用鼠标抓住直接旋转。动画也不用做了。
但是surface上画曲线,这个问题仔细想一下,相当的不容易。surface和曲线不能是两个独立的object,否则会互相遮挡。把surface设成半透明的,这也不好。效果和wireframe差不多了。道理上也是不对的。
一种方法是把曲线的每一段作为surface patch的一个边,那需要把surface的patch重新划分,这很复杂。
另一种方法是OpenGL的texture方式,相当于贴膜。这个方法也有问题。
x1


-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#30 Re: 贴个图
看来我想复杂了。这个图最后用Python Plotly解决了。TheMatrix 写了: 2023年 11月 6日 12:39 一种方法是把曲线的每一段作为surface patch的一个边,那需要把surface的patch重新划分,这很复杂。
另一种方法是OpenGL的texture方式,相当于贴膜。这个方法也有问题。
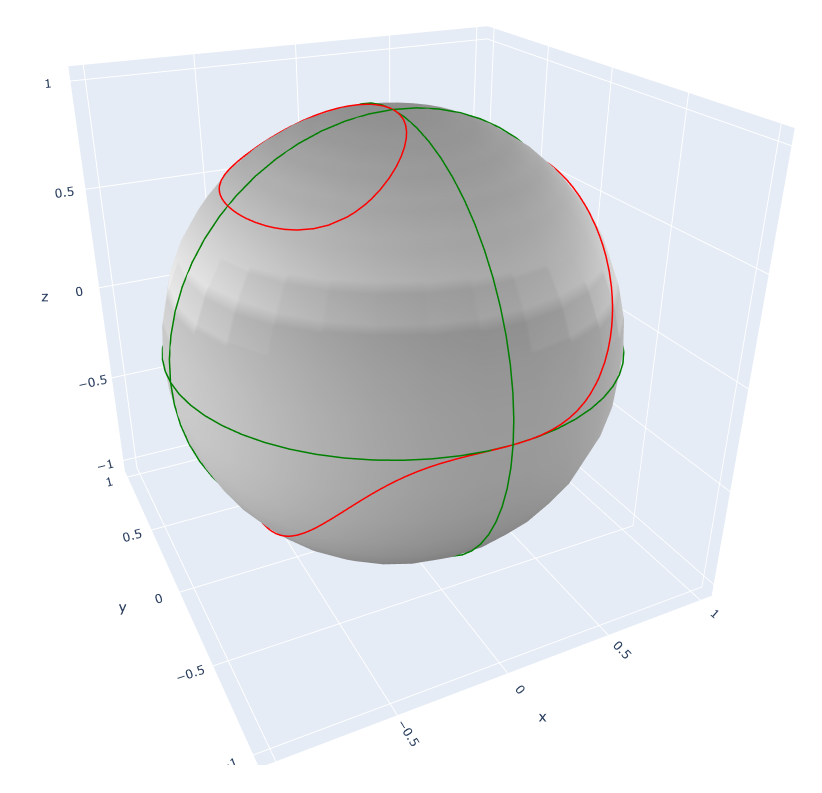
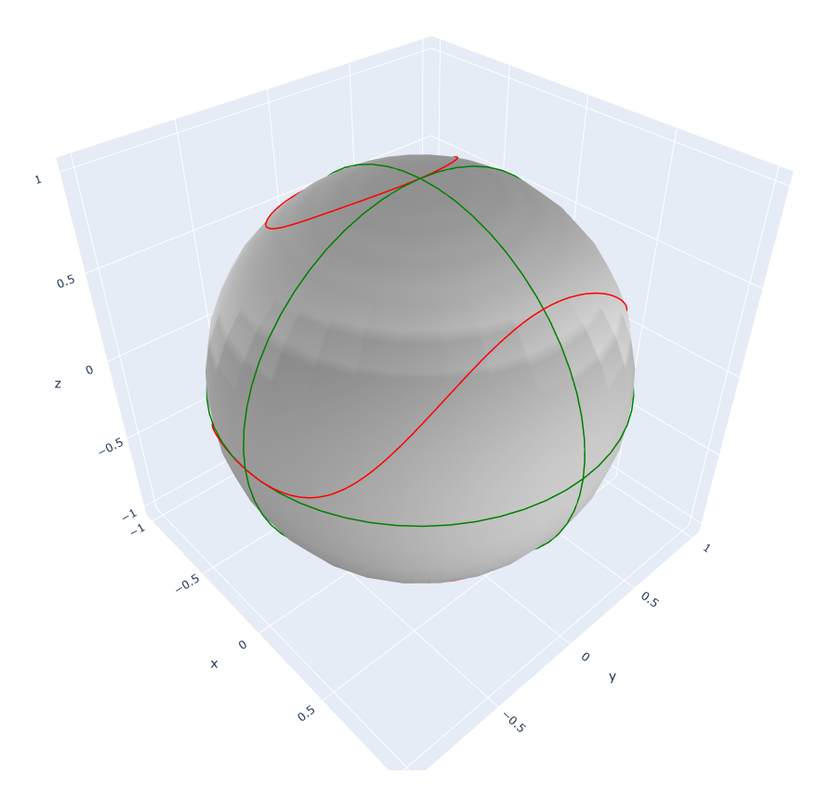
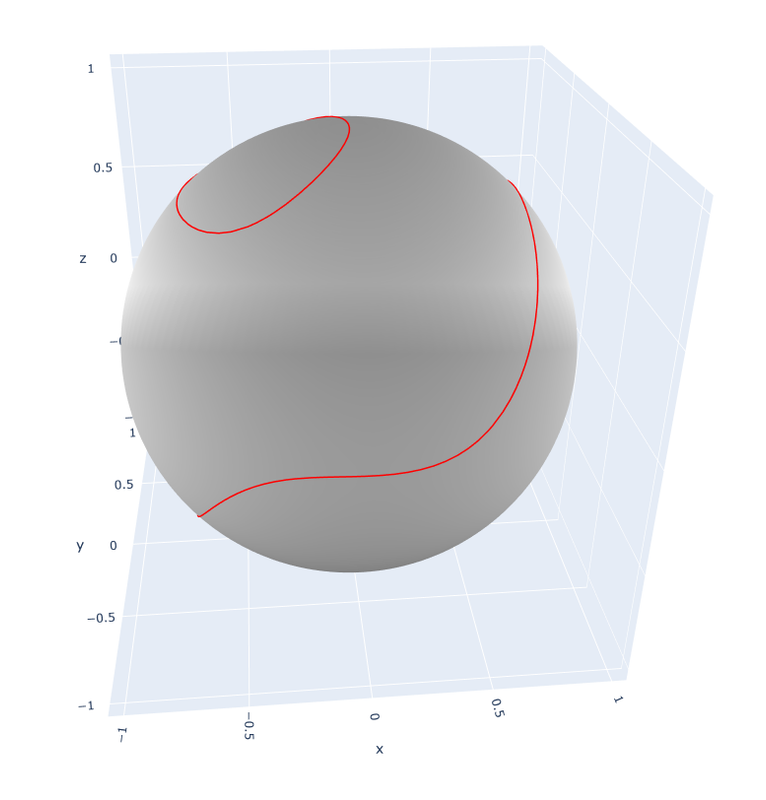
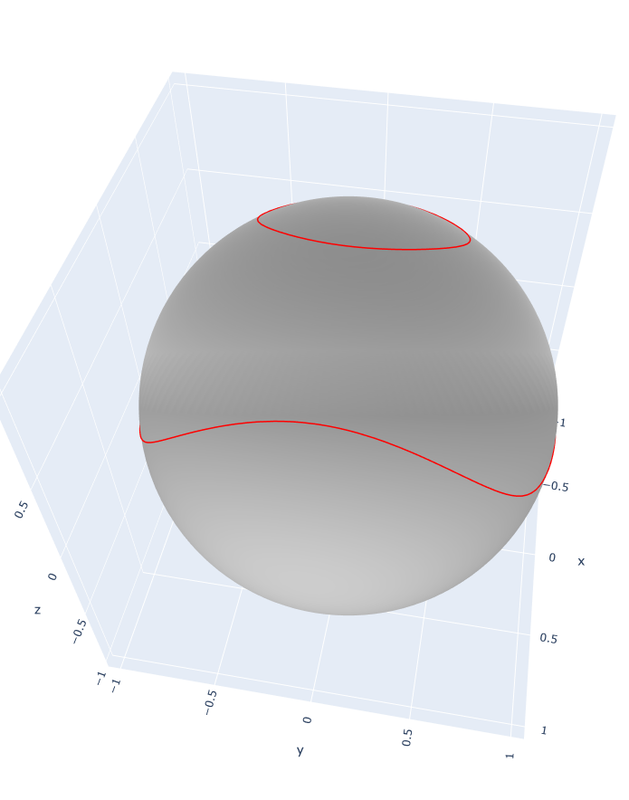
Matplotlib据说不是true 3d。它没有把line当成true 3d object。而surface是true 3d object。在surface前面画线看不见,因为它的z-order是不对的。
据说Plotly是true 3d。所以我试了一下Python Plotly,果然。直接在surface上画线就行了。我想复杂了。
Plotly的3d图也能鼠标转动。想看什么角度就看什么角度。效果相当不错。
以后我改用Plotly了。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#32 Re: 贴个图
直纹面的来了。TheMatrix 写了: 2023年 11月 5日 09:41 肯定能。我试过,但是效果很不好。
其实画直纹面,对这个问题是很有意义的。因为直纹面才是这个问题里面真正的“物体”。
如果能3D打印出来就更好了。这就是真正的形象化的学数学了。
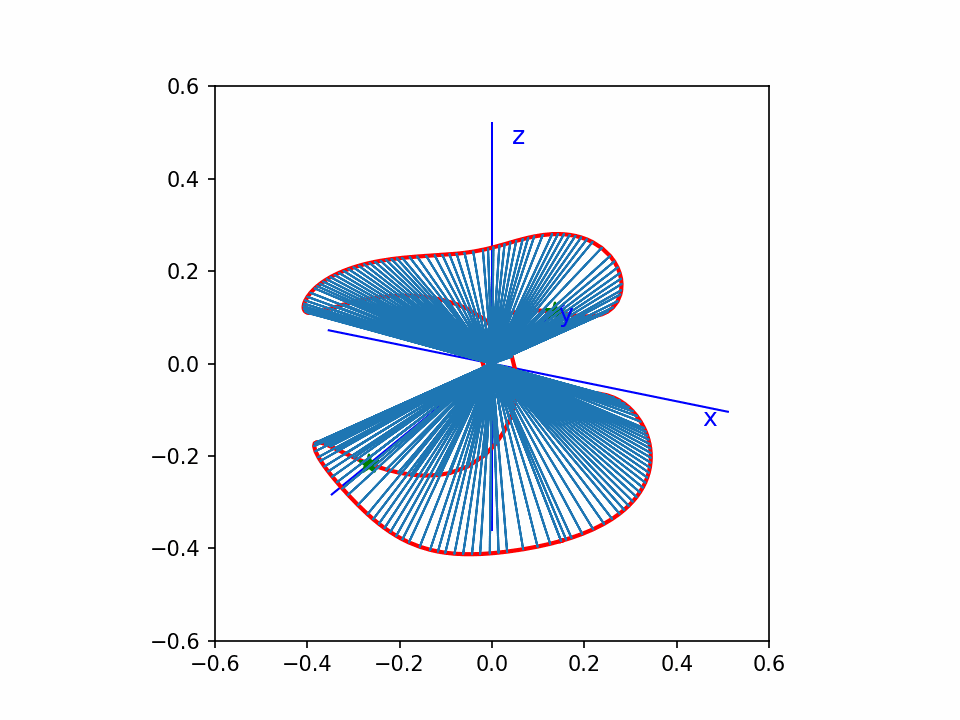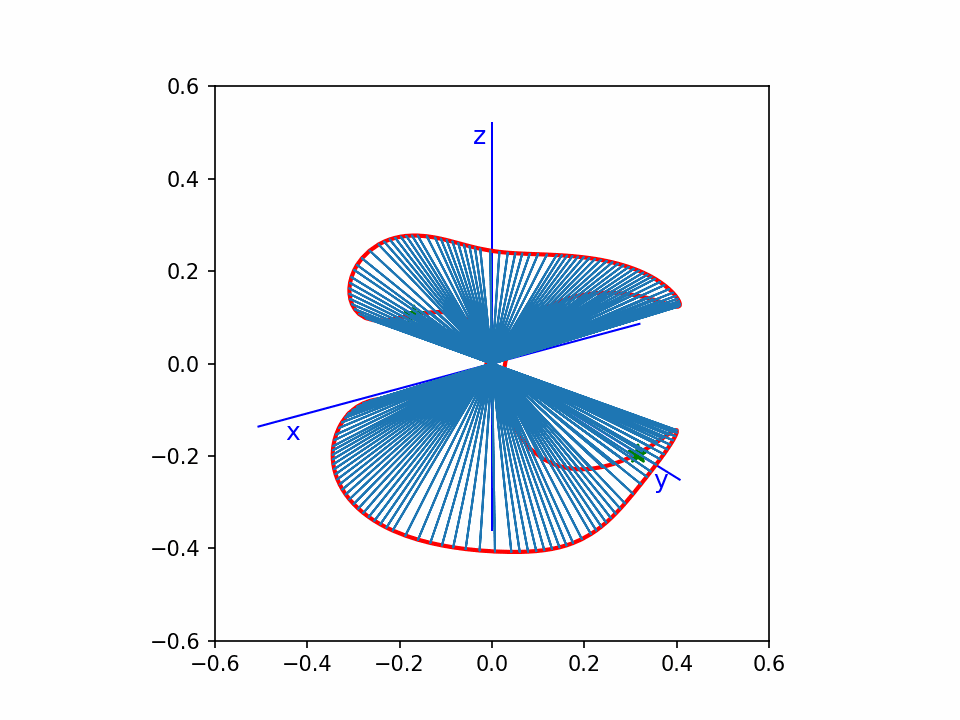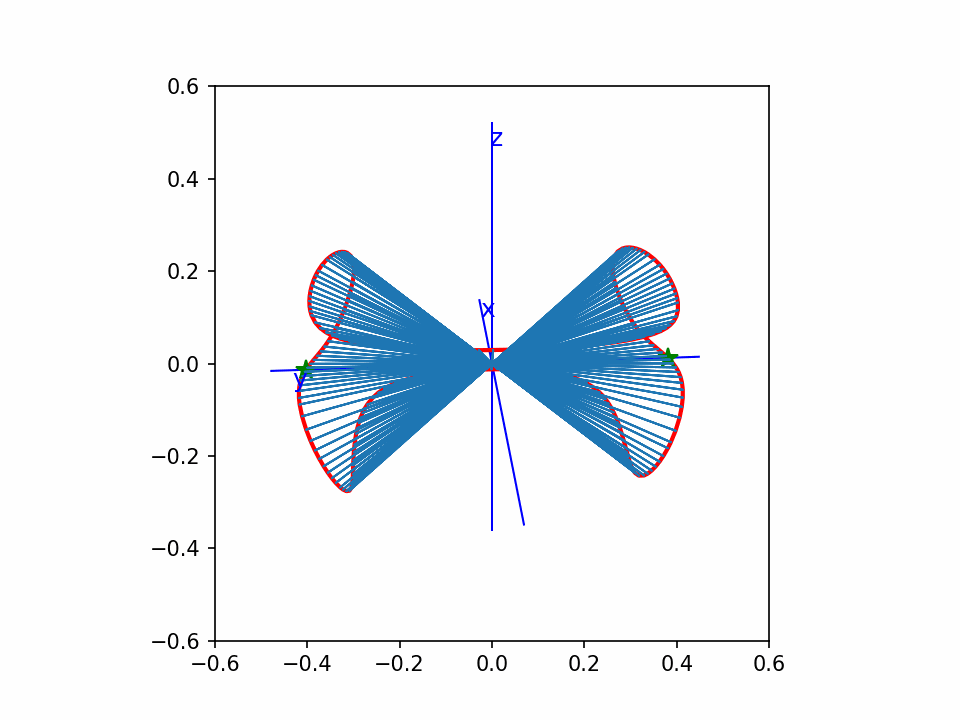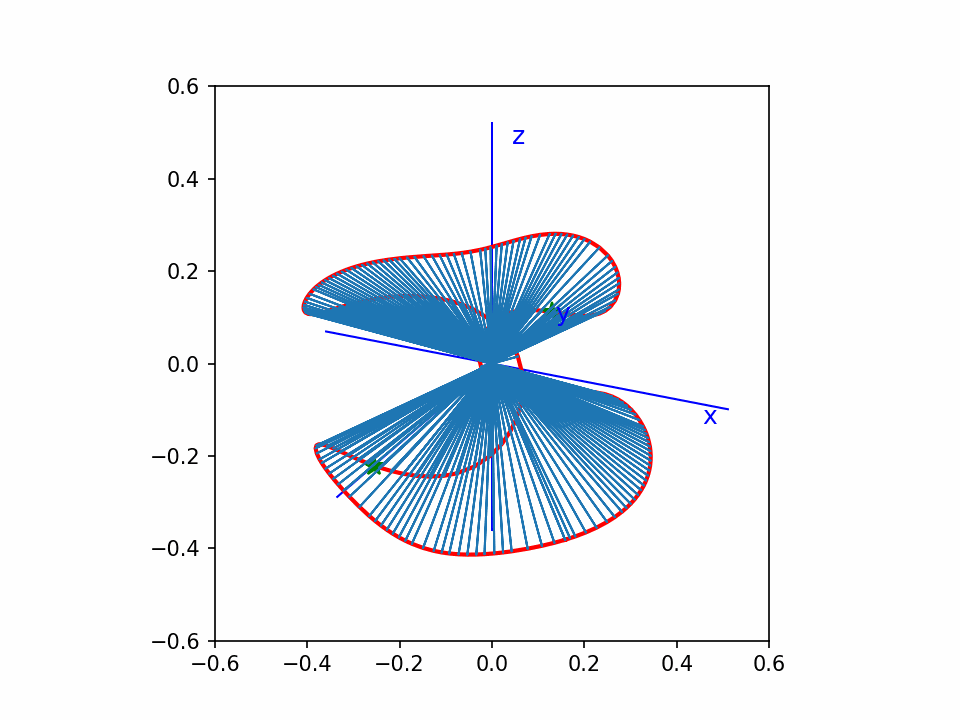
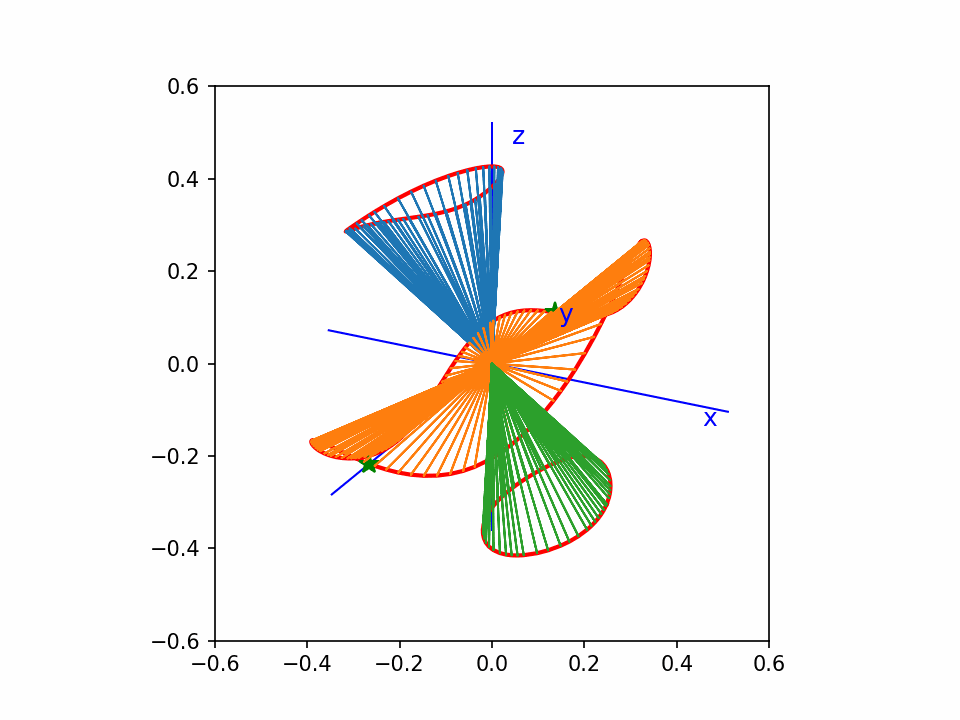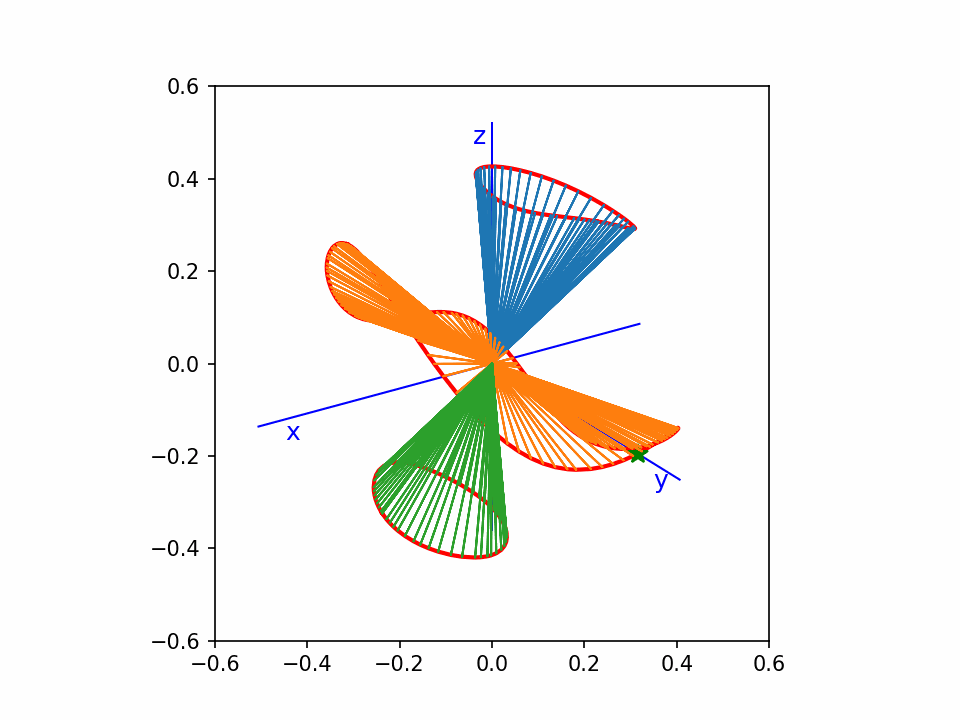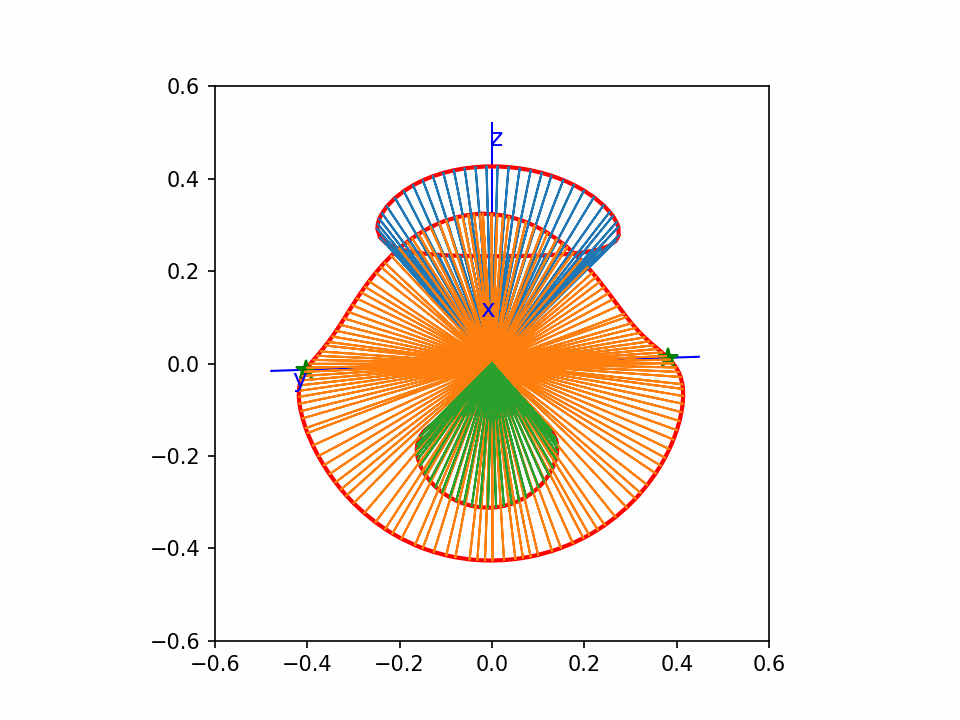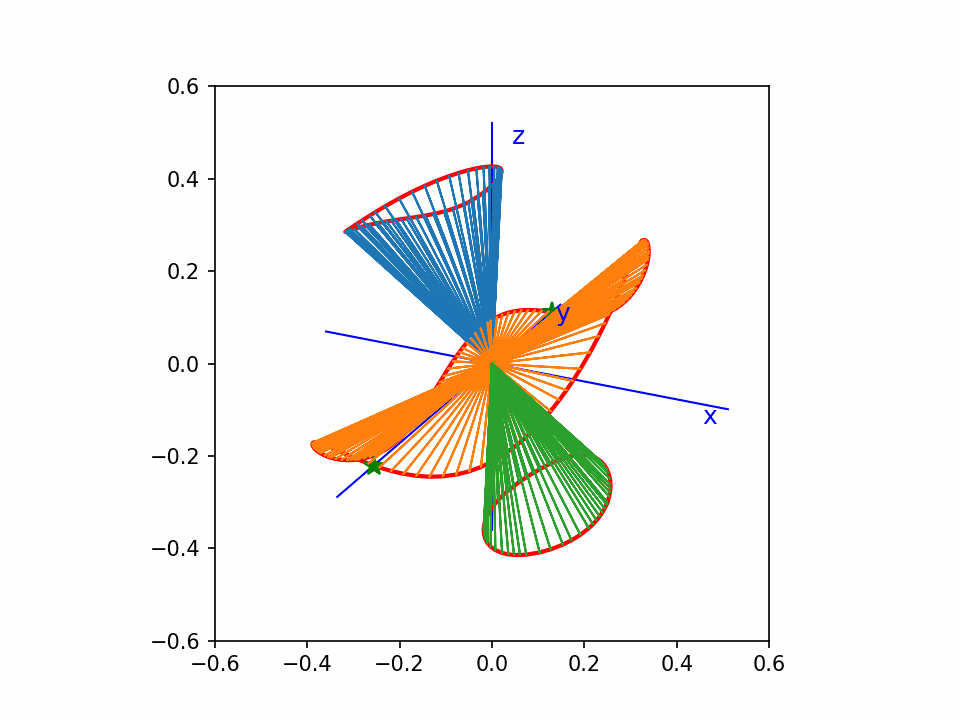
这个是 y2=x3-x 的齐次化直纹面,绕z-轴旋转。
这个还是matplotlib画的点线图,没有遮挡效果,看着比较乱。但是动起来还能看。
从这个动图可以看出,曲线上的点,我基本上做到了均匀分布。
比我以前画的一个效果好。因为以前那个没有做到均匀分布。另外这个图直线都截取到单位球面,比较统一。
中间一片像个木耳。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35