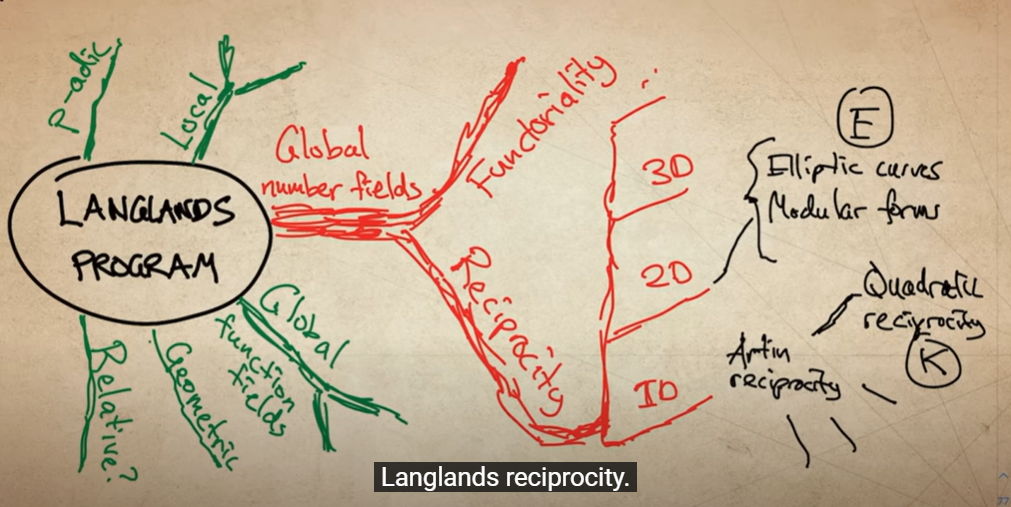
Matthew Emerton是他说的‘世界上懂最多Langlands program的人“。
出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
版主: verdelite, TheMatrix
#22 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
这个视频主是Andreas Holmstrom,现在挪威,在他的网站PeakMath.org上可以找到。
Matthew Emerton是他说的‘世界上懂最多Langlands program的人“。
Matthew Emerton是他说的‘世界上懂最多Langlands program的人“。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#25 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
Adeles and ideles 确实是比较复杂的代数结构。作者专门写了两段评述:
We close this discussion by a recapitulation of the role of the adeles in this
argument, and, more generally, in contemporary number theory. Like many mathematical innovations, the use of the adeles at first seems to be a merely technical
device, which one becomes used to over time; and which one might eventually regard as natural and even intuitive, just through habit alone. There is certainly an
aspect of this with regard to the use of the adeles, and I believe that it reflects the
attitude of many, perhaps even most, students of number theory upon encountering
them for the first time. And the adeles do have many advantages which appear
purely technical at first; e.g. as we already indicated (in footnote 16 above), one
such advantage is that we get to replace the ring Z with the field Q. It seems, then,
worthwhile to reflect on what fundamental number theoretic ideas and intuitions
might be being captured in the concept of the adeles, beyond their purely technical
advantages. We conclude with a short series of remarks in this spirit:
The product structure of the adeles, a structural product in the sense of modern
algebra, reflects in a subtle but important way the literal, arithmetic product that
appears in the statement of the fundamental theorem of arithmetic (that any natural number factors uniquely as a product of prime powers). The restricted nature
of the product reflects the boundedness of the denominator of any rational number.
And even though Q is a field, and so in some sense has no intrinsic arithmetic (unlike the ring Z), the primes are still present and making their influence felt, once we
consider the embedding Q → A. One might summarize these points by saying that
the embedding Q → A “externalizes” the traditional arithmetic concepts of prime
number, unique factorization, and boundedness of denominators, and reinterprets
them in a framework which more comfortably accommodates the mores of modern
algebra, which require one to manipulate rings and fields themselves, rather than
their individual elements.
#26 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
我一直没学懂,但感觉Adeles and ideles 不是太复杂,就是把所有local的东西都放在一起的一种形式。
大家如果有兴趣,可以来讨论。
大家如果有兴趣,可以来讨论。
TheMatrix 写了: 2023年 12月 24日 10:08 Adeles and ideles 确实是比较复杂的代数结构。作者专门写了两段评述:
We close this discussion by a recapitulation of the role of the adeles in this
argument, and, more generally, in contemporary number theory. Like many mathematical innovations, the use of the adeles at first seems to be a merely technical
device, which one becomes used to over time; and which one might eventually regard as natural and even intuitive, just through habit alone. There is certainly an
aspect of this with regard to the use of the adeles, and I believe that it reflects the
attitude of many, perhaps even most, students of number theory upon encountering
them for the first time. And the adeles do have many advantages which appear
purely technical at first; e.g. as we already indicated (in footnote 16 above), one
such advantage is that we get to replace the ring Z with the field Q. It seems, then,
worthwhile to reflect on what fundamental number theoretic ideas and intuitions
might be being captured in the concept of the adeles, beyond their purely technical
advantages. We conclude with a short series of remarks in this spirit:
The product structure of the adeles, a structural product in the sense of modern
algebra, reflects in a subtle but important way the literal, arithmetic product that
appears in the statement of the fundamental theorem of arithmetic (that any natural number factors uniquely as a product of prime powers). The restricted nature
of the product reflects the boundedness of the denominator of any rational number.
And even though Q is a field, and so in some sense has no intrinsic arithmetic (unlike the ring Z), the primes are still present and making their influence felt, once we
consider the embedding Q → A. One might summarize these points by saying that
the embedding Q → A “externalizes” the traditional arithmetic concepts of prime
number, unique factorization, and boundedness of denominators, and reinterprets
them in a framework which more comfortably accommodates the mores of modern
algebra, which require one to manipulate rings and fields themselves, rather than
their individual elements.
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#27 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
我也不懂。这两个词我的感觉是:conglomerate。FoxMe 写了: 2023年 12月 24日 10:53 我一直没学懂,但感觉Adeles and ideles 不是太复杂,就是把所有local的东西都放在一起的一种形式。
大家如果有兴趣,可以来讨论。
他的这段评论,我觉得还要提到拓扑上合拍。A看起来就是一个product of Qp,但是Q和Qp拓扑上是不同的,一个是阿基米德norm,一个是非阿基米德norm,强行embedding,就不可能同时尊重两个拓扑。但是把Qp conglomerate到一起,这上面是有拓扑的,对吧?再embedding Q --> A,就尊重了拓扑结构。这应该是一种diagonal embedding。
#28 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
差不多,我还没领会。
Adele是一个歌手的名字,中文翻译为阿黛尔。喜欢一首忧伤的情歌Someone Like You
Adele是一个歌手的名字,中文翻译为阿黛尔。喜欢一首忧伤的情歌Someone Like You
TheMatrix 写了: 2023年 12月 24日 12:47 我也不懂。这两个词我的感觉是:conglomerate。
他的这段评论,我觉得还要提到拓扑上合拍。A看起来就是一个product of Qp,但是Q和Qp拓扑上是不同的,一个是阿基米德norm,一个是非阿基米德norm,强行embedding,就不可能同时尊重两个拓扑。但是把Qp conglomerate到一起,这上面是有拓扑的,对吧?再embedding Q --> A,就尊重了拓扑结构。这应该是一种diagonal embedding。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#29 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
ideles class group和ideal class group比较相似。TheMatrix 写了: 2023年 12月 24日 10:08 Adeles and ideles 确实是比较复杂的代数结构。作者专门写了两段评述:
We close this discussion by a recapitulation of the role of the adeles in this
argument, and, more generally, in contemporary number theory. Like many mathematical innovations, the use of the adeles at first seems to be a merely technical
device, which one becomes used to over time; and which one might eventually regard as natural and even intuitive, just through habit alone. There is certainly an
aspect of this with regard to the use of the adeles, and I believe that it reflects the
attitude of many, perhaps even most, students of number theory upon encountering
them for the first time. And the adeles do have many advantages which appear
purely technical at first; e.g. as we already indicated (in footnote 16 above), one
such advantage is that we get to replace the ring Z with the field Q. It seems, then,
worthwhile to reflect on what fundamental number theoretic ideas and intuitions
might be being captured in the concept of the adeles, beyond their purely technical
advantages. We conclude with a short series of remarks in this spirit:
The product structure of the adeles, a structural product in the sense of modern
algebra, reflects in a subtle but important way the literal, arithmetic product that
appears in the statement of the fundamental theorem of arithmetic (that any natural number factors uniquely as a product of prime powers). The restricted nature
of the product reflects the boundedness of the denominator of any rational number.
And even though Q is a field, and so in some sense has no intrinsic arithmetic (unlike the ring Z), the primes are still present and making their influence felt, once we
consider the embedding Q → A. One might summarize these points by saying that
the embedding Q → A “externalizes” the traditional arithmetic concepts of prime
number, unique factorization, and boundedness of denominators, and reinterprets
them in a framework which more comfortably accommodates the mores of modern
algebra, which require one to manipulate rings and fields themselves, rather than
their individual elements.
ideal class group,我觉得可以说是一种度量,看一个integral domain距离一个principal ideal domain有多远。Principal ideal domain比较好处理。而ideal class group可以说是度量一个integral domain的处理难度。
在完全general的setting下,假设有一个integral domain R。它有一个field of fraction F,也就是 r/s 形式的元素。F可以看成是一个R-module。R本身也可以看成是一个R-module。
R本身看成R-module的话,其ideal可以看成是R-submodule。F作为R-module的话,它也有R-submodule,沿用ideal的称呼,就叫fractional ideal,因为里面的元素都是fraction。
F里全部的fractional ideal的集合,有加法,有乘法,构成一个ring,the ring of fractional ideals,而且是个integral domain。这个ring的group of units,也就是所有的有逆元素的fractional ideals,叫ideal group。这是一个abelian group。- 什么样的fractional ideal作为元素有逆元素,这要看乘法的定义。乘法的定义,基本上就是fraction相乘。
ideal group这个abelian group,其中包含一个subgroup,由principal fractional ideal组成,也就是由单一元素r/s生成的fractional ideal,或者说由单一元素生成的R-submodule - 这些很明显是可逆的,所以是subgroup。
ideal class group,就是ideal group modulo the subgroup of principal fractional ideals。
我在往ideles class group那里走,还没有完全走通。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#31 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
ideal class group是代数数论的基本问题之一。
idele class group我也在看。idele是法语ideal element的缩写。
idele class group我也在看。idele是法语ideal element的缩写。
TheMatrix 写了: 2023年 12月 25日 18:53 ideles class group和ideal class group比较相似。
ideal class group,我觉得可以说是一种度量,看一个integral domain距离一个principal ideal domain有多远。Principal ideal domain比较好处理。而ideal class group可以说是度量一个integral domain的处理难度。
在完全general的setting下,假设有一个integral domain R。它有一个field of fraction F,也就是 r/s 形式的元素。F可以看成是一个R-module。R本身也可以看成是一个R-module。
R本身看成R-module的话,其ideal可以看成是R-submodule。F作为R-module的话,它也有R-submodule,沿用ideal的称呼,就叫fractional ideal,因为里面的元素都是fraction。
F里全部的fractional ideal的集合,有加法,有乘法,构成一个ring,the ring of fractional ideals,而且是个integral domain。这个ring的group of units,也就是所有的有逆元素的fractional ideals,叫ideal group。这是一个abelian group。- 什么样的fractional ideal作为元素有逆元素,这要看乘法的定义。乘法的定义,基本上就是fraction相乘。
ideal group这个abelian group,其中包含一个subgroup,由principal fractional ideal组成,也就是由单一元素r/s生成的fractional ideal,或者说由单一元素生成的R-submodule - 这些很明显是可逆的,所以是subgroup。
ideal class group,就是ideal group modulo the subgroup of principal fractional ideals。
我在往ideles class group那里走,还没有完全走通。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#32 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
我上面说的fractional ideal少了一个限定条件:这个ideal要能够被clear denominator by a single element r in R,也就是分母中出现的素数有限。应该也可以说是finitely generated R-submodule。TheMatrix 写了: 2023年 12月 25日 18:53 ideles class group和ideal class group比较相似。
ideal class group,我觉得可以说是一种度量,看一个integral domain距离一个principal ideal domain有多远。Principal ideal domain比较好处理。而ideal class group可以说是度量一个integral domain的处理难度。
在完全general的setting下,假设有一个integral domain R。它有一个field of fraction F,也就是 r/s 形式的元素。F可以看成是一个R-module。R本身也可以看成是一个R-module。
R本身看成R-module的话,其ideal可以看成是R-submodule。F作为R-module的话,它也有R-submodule,沿用ideal的称呼,就叫fractional ideal,因为里面的元素都是fraction。
F里全部的fractional ideal的集合,有加法,有乘法,构成一个ring,the ring of fractional ideals,而且是个integral domain。这个ring的group of units,也就是所有的有逆元素的fractional ideals,叫ideal group。这是一个abelian group。- 什么样的fractional ideal作为元素有逆元素,这要看乘法的定义。乘法的定义,基本上就是fraction相乘。
ideal group这个abelian group,其中包含一个subgroup,由principal fractional ideal组成,也就是由单一元素r/s生成的fractional ideal,或者说由单一元素生成的R-submodule - 这些很明显是可逆的,所以是subgroup。
ideal class group,就是ideal group modulo the subgroup of principal fractional ideals。
我在往ideles class group那里走,还没有完全走通。
这和idele class group的要求对上了。Adele ring的要求是product中只有有限个fraction。相当于fractional ideal中要求可以被一个数clear denominator。
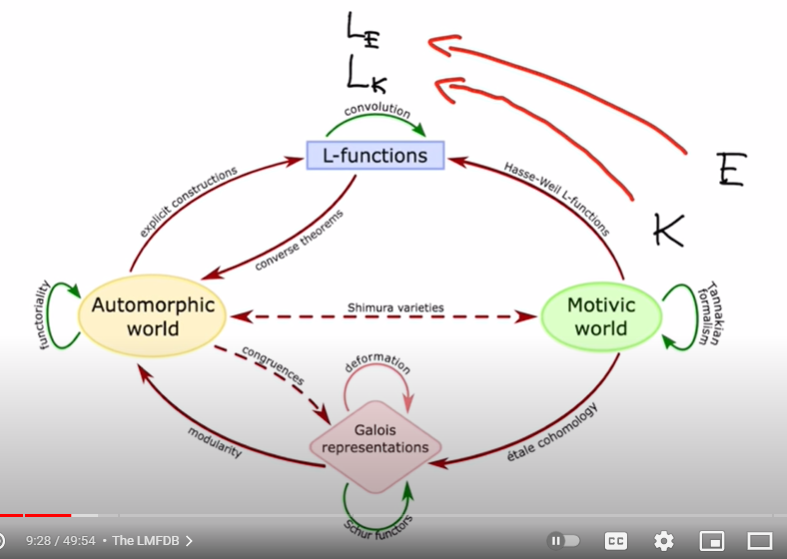
ideal class group和idele class group基本上差不多,好像说都能处理同样的事情。好像说idele class group是更现代的方法。在number field上,Dedekind推广了Dirichlet L-function,其中用的系数,既可以用ideal class group定义(Hecke),也可以用idele class group定义(Tate)。这两种方法中的系数,都叫character,是Dirichlet character的推广,是ideal class group或idele class group到unitary complex number的group homomorphism。
凡是从character这边来的L-function,就叫automorphic。另一边是从代数方程在有限域下解的个数中来的,叫motivic。Motivic这边和Galois group关系很大。Automorphic <---> Motivic/Galois group 之间的对应关系(猜想中),就是Langlands reciprocity。
#33 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
很好的总结,帮我厘清了好几个概念。关于adeles and ideles,你们有没有比较好的书推荐?
TheMatrix 写了: 2023年 12月 26日 21:55 我上面说的fractional ideal少了一个限定条件:这个ideal要能够被clear denominator by a single element r in R,也就是分母中出现的素数有限。应该也可以说是finitely generated R-submodule。
这和idele class group的要求对上了。Adele ring的要求是product中只有有限个fraction。相当于fractional ideal中要求可以被一个数clear denominator。
ideal class group和idele class group基本上差不多,好像说都能处理同样的事情。好像说idele class group是更现代的方法。在number field上,Dedekind推广了Dirichlet L-function,其中用的系数,既可以用ideal class group定义(Hecke),也可以用idele class group定义(Tate)。这两种方法中的系数,都叫character,是Dirichlet character的推广,是ideal class group或idele class group到unitary complex number的group homomorphism。
凡是从character这边来的L-function,就叫automorphic。另一边是从代数方程在有限域下解的个数中来的,叫motivic。Motivic这边和Galois group关系很大。Automorphic <---> Motivic/Galois group 之间的对应关系(猜想中),就是Langlands reciprocity。
#34 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
看了,语速太慢了,以2倍速度播放才好。
明白了L函数不仅形成环(有加法乘法;乘法没太看懂,似乎是系数逐项相乘再修正),而且是内积空间(primitive L-functions形成一组基)。这些性质很强。
明白了L函数不仅形成环(有加法乘法;乘法没太看懂,似乎是系数逐项相乘再修正),而且是内积空间(primitive L-functions形成一组基)。这些性质很强。
#35 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
限制为有限个,就是locally compact,很好。
TheMatrix 写了: 2023年 12月 26日 21:55 我上面说的fractional ideal少了一个限定条件:这个ideal要能够被clear denominator by a single element r in R,也就是分母中出现的素数有限。应该也可以说是finitely generated R-submodule。
这和idele class group的要求对上了。Adele ring的要求是product中只有有限个fraction。相当于fractional ideal中要求可以被一个数clear denominator。
ideal class group和idele class group基本上差不多,好像说都能处理同样的事情。好像说idele class group是更现代的方法。在number field上,Dedekind推广了Dirichlet L-function,其中用的系数,既可以用ideal class group定义(Hecke),也可以用idele class group定义(Tate)。这两种方法中的系数,都叫character,是Dirichlet character的推广,是ideal class group或idele class group到unitary complex number的group homomorphism。
凡是从character这边来的L-function,就叫automorphic。另一边是从代数方程在有限域下解的个数中来的,叫motivic。Motivic这边和Galois group关系很大。Automorphic <---> Motivic/Galois group 之间的对应关系(猜想中),就是Langlands reciprocity。
#36 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
class field theory的书里一般都有,但是不好懂,我也没学过
https://www.jmilne.org/math/CourseNotes/CFT.pdf
https://kskedlaya.org/cft/ch_adelic.html
https://www.jmilne.org/math/CourseNotes/CFT.pdf
https://kskedlaya.org/cft/ch_adelic.html
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#37 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
对。locally compact就能定义Haar measure,然后就能在group上积分,还能做傅里叶变换,傅里叶变换的单元是character,而character又是L-function的系数。互相都联系上了。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#38 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
哦。第一本书我有。这个人写了一系列的书,都是随便下载的。FoxMe 写了: 2023年 12月 27日 10:00 class field theory的书里一般都有,但是不好懂,我也没学过
https://www.jmilne.org/math/CourseNotes/CFT.pdf
https://kskedlaya.org/cft/ch_adelic.html
#39 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
这篇文章看到这里了,初步了解了Adele的好处:可以直接把L函数表示为Euler product. 但是下面这两段话还没有完全理解。
TheMatrix 写了: 2023年 12月 24日 10:08 Adeles and ideles 确实是比较复杂的代数结构。作者专门写了两段评述:
We close this discussion by a recapitulation of the role of the adeles in this
argument, and, more generally, in contemporary number theory. Like many mathematical innovations, the use of the adeles at first seems to be a merely technical
device, which one becomes used to over time; and which one might eventually regard as natural and even intuitive, just through habit alone. There is certainly an
aspect of this with regard to the use of the adeles, and I believe that it reflects the
attitude of many, perhaps even most, students of number theory upon encountering
them for the first time. And the adeles do have many advantages which appear
purely technical at first; e.g. as we already indicated (in footnote 16 above), one
such advantage is that we get to replace the ring Z with the field Q. It seems, then,
worthwhile to reflect on what fundamental number theoretic ideas and intuitions
might be being captured in the concept of the adeles, beyond their purely technical
advantages. We conclude with a short series of remarks in this spirit:
The product structure of the adeles, a structural product in the sense of modern
algebra, reflects in a subtle but important way the literal, arithmetic product that
appears in the statement of the fundamental theorem of arithmetic (that any natural number factors uniquely as a product of prime powers). The restricted nature
of the product reflects the boundedness of the denominator of any rational number.
And even though Q is a field, and so in some sense has no intrinsic arithmetic (unlike the ring Z), the primes are still present and making their influence felt, once we
consider the embedding Q → A. One might summarize these points by saying that
the embedding Q → A “externalizes” the traditional arithmetic concepts of prime
number, unique factorization, and boundedness of denominators, and reinterprets
them in a framework which more comfortably accommodates the mores of modern
algebra, which require one to manipulate rings and fields themselves, rather than
their individual elements.
#40 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
继续看, 知道了什么事motivic zeta-function.
Langlands Program基本上是代数数论中的解析数论,但是其中的motivic 更广泛。从数域推广到环,再推广到variety和scheme,都可以定义zeta-function. 和代数几何联系上了。
Langlands Program基本上是代数数论中的解析数论,但是其中的motivic 更广泛。从数域推广到环,再推广到variety和scheme,都可以定义zeta-function. 和代数几何联系上了。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 265
- 帖子: 13377
- 注册时间: 2022年 7月 26日 00:35
#41 Re: 出个和Langlands Program相关的题,下面的数列接下来十位分别是什么?
motivic L-function 就是可以看成是代数方程 modulo p 然后数解的个数而得到的 L-function 吧?FoxMe 写了: 2023年 12月 29日 09:59 继续看, 知道了什么事motivic zeta-function.
Langlands Program基本上是代数数论中的解析数论,但是其中的motivic 更广泛。从数域推广到环,再推广到variety和scheme,都可以定义zeta-function. 和代数几何联系上了。