其实在TheMatrix 写了: 2025年 3月 20日 16:10 bnf (f: state --> state) 作为状态空间上的自变换,美则美矣,因为它简单,但是丧失了一些信息。
自变量是一个state,这是没问题的。但是函数值不仅仅是一个新的state,还包括很多信息。比如path,从起始的state怎么一步一步到达新的state。如果加上这些,就变成:f: state --> path, where path is a list of state。这就不再是state空间上的自变换了。
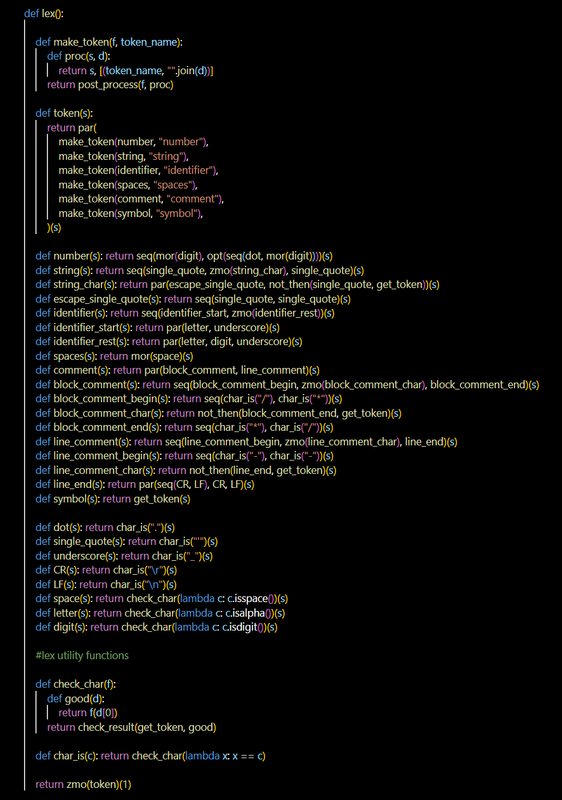
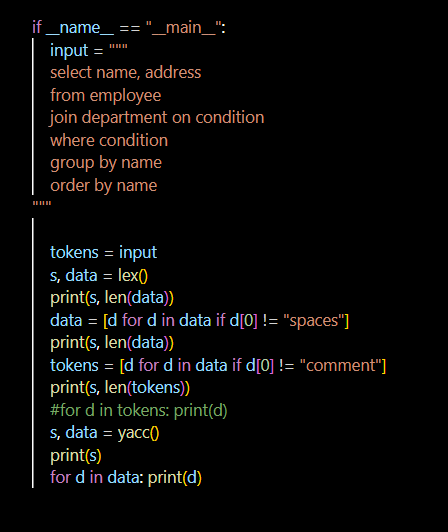
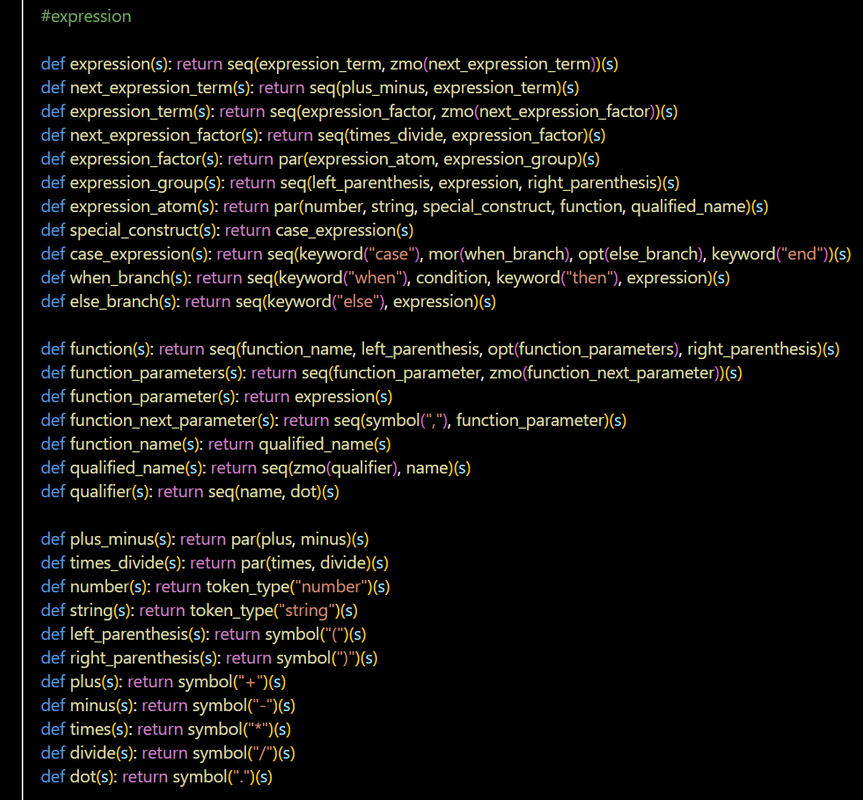
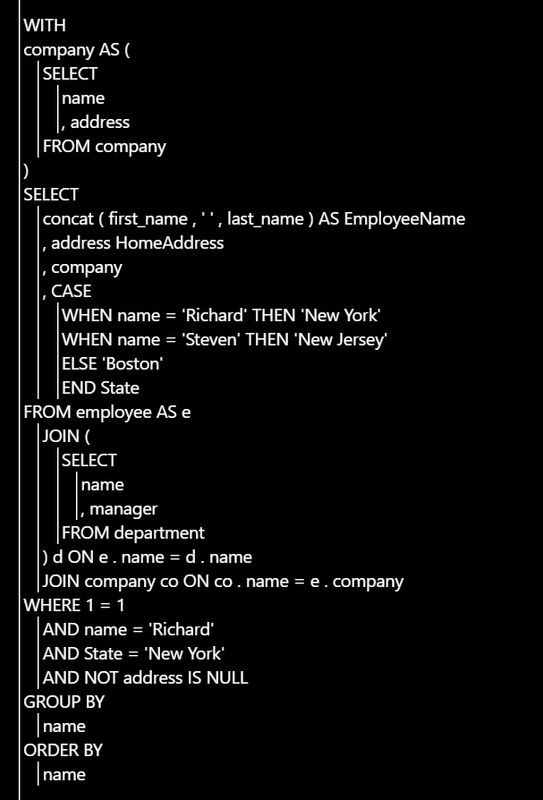
自变换的好处是可以有composition。但是也没必要执着于它。它是什么就是什么。f: state --> state 这个抽象对于识别一个语法true/false是够了。但是没有更多的信息。
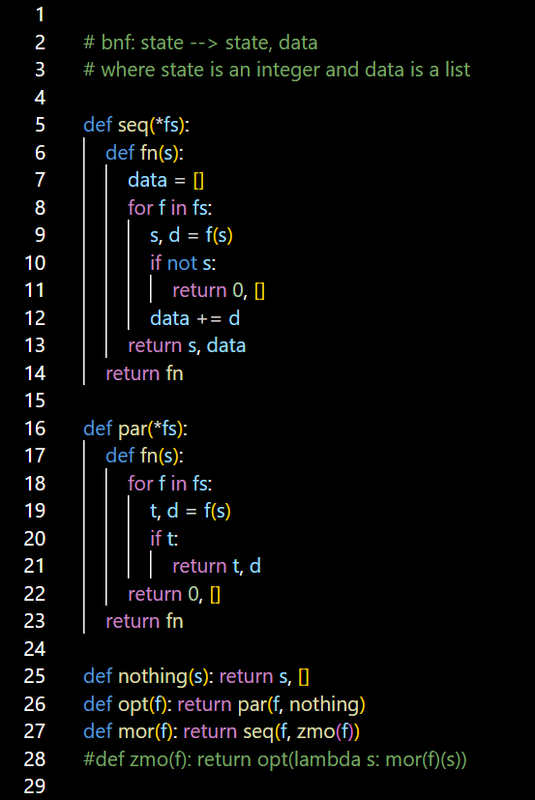
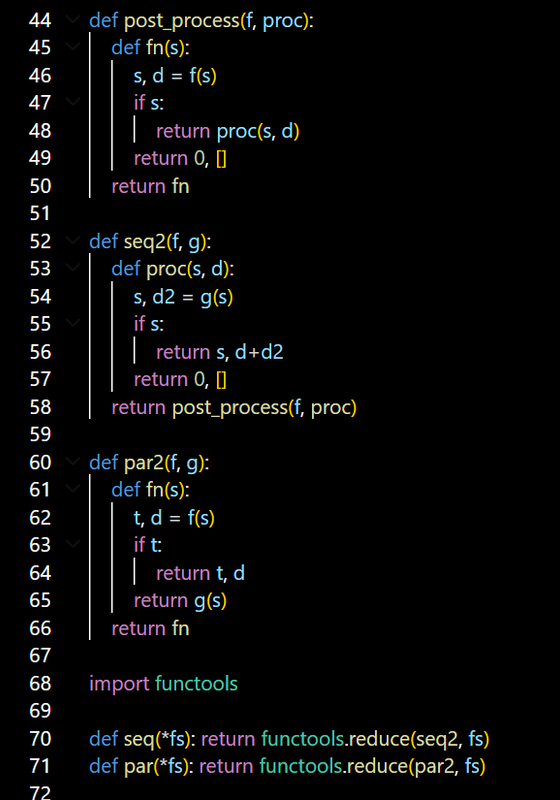
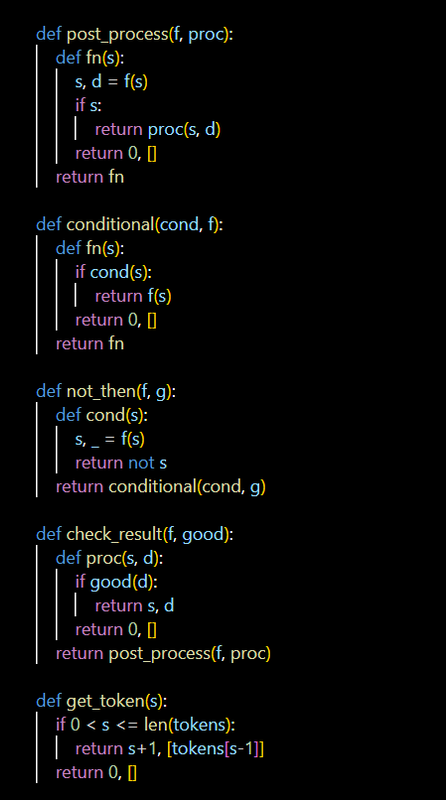
从 f: state --> (state, X) 出发,seq要做的,是把这样的一些函数串在一起,函数结果也要串在一起。结果要串在一起的话,说明X必须是一个list。list of what? 为了保持最大的通用性,就不明确的说list of what了,可以是list of anything,可以是list of list。
所以这两天我想来想去,又回到我之前给出的函数signature了:
f: state --> (state, [])
{ f: state --> (state, []) }
空间上,seq和par仍然构成一个algebra。seq是乘法,par是加法。结合律和分配律仍然成立,没有交换律。
seq和par也构成图灵完备的程序结构。seq是顺序执行,par是分支。loop不需要,因为可以用递归。
所以这可以叫“程序algebra”。
我原来用的函数signature是 f: p --> (p, []),其中p是文本cursor位置。在parser的问题下,等价于state。这次我把p换成state,在一般的状态空间中考虑,state的编号可以不连续。