新未名空间

rgg 写了： 2023年 1月 5日 09:41 你说得对。explicitly 写出矩阵表示，还是挺难。

我在用permutation character/representation做。群作用在某subgroup coset上。permutation representation群矩阵简单，每行只有一个元素，而且是1。

我在找Symm(5)的6维不可约表示。我找到一个20维的permutation representation，按照character table分解，里面有一个trivial character，两个4维character（不同的），一个5维character，和一个6维的character。

我发现：
1，不管几维的表示，每个元素的eigenvalue都是root of unity，和群元素的阶有关。这个比较好理解。
2，每个矩阵都能完全对角化 - 相似对角化。也就是全部eigenvector span。这个应该也是定理吧？

所以在20维中找6维不可约表示，也就是找6维的公共不可约不变子空间，是一个组合问题。这里有对称性，但比较纷乱。

TheMatrix 写了： 2023年 1月 5日 12:01 我在用permutation character/representation做。群作用在某subgroup coset上。permutation representation群矩阵简单，每行只有一个元素，而且是1。

我在找Symm(5)的6维不可约表示。我找到一个20维的permutation representation，按照character table分解，里面有一个trivial character，两个4维character（不同的），一个5维character，和一个6维的character。

我发现：
1，不管几维的表示，每个元素的eigenvalue都是root of unity，和群元素的阶有关。这个比较好理解。
2，每个矩阵都能完全对角化 - 相似对角化。也就是全部eigenvector span。这个应该也是定理吧？

所以在20维中找6维不可约表示，也就是找6维的公共不可约不变子空间，是一个组合问题。这里有对称性，但比较纷乱。

我想这多半是个解决了的问题。 查了查例如这个软件有这个功能：
https://www.gap-system.org/Overview/Cap ... tions.html
https://docs.gap-system.org/doc/ref/cha ... C6846718D9

TheMatrix 写了： 2023年 1月 5日 12:01 我在用permutation character/representation做。群作用在某subgroup coset上。permutation representation群矩阵简单，每行只有一个元素，而且是1。

我在找Symm(5)的6维不可约表示。我找到一个20维的permutation representation，按照character table分解，里面有一个trivial character，两个4维character（不同的），一个5维character，和一个6维的character。

我发现：
1，不管几维的表示，每个元素的eigenvalue都是root of unity，和群元素的阶有关。这个比较好理解。
2，每个矩阵都能完全对角化 - 相似对角化。也就是全部eigenvector span。这个应该也是定理吧？

所以在20维中找6维不可约表示，也就是找6维的公共不可约不变子空间，是一个组合问题。这里有对称性，但比较纷乱。

Every permutation matrix A is diagonalizable, since A commutes with its transpose A^T (which agrees with the inverse of A). In general, a matrix commutes with its conjugate transpose if and only if it is diagonalizable by an orthogonal matric.

rgg 写了： 2023年 1月 5日 12:20 我想这多半是个解决了的问题。 查了查例如这个软件有这个功能：
https://www.gap-system.org/Overview/Cap ... tions.html
https://docs.gap-system.org/doc/ref/cha ... C6846718D9

我想应该是的。我只是编程序for fun。

YWY 写了： 2023年 1月 5日 12:23 Every permutation matrix A is diagonalizable, since A commutes with its transpose A^T (which agrees with the inverse of A). In general, a matrix commutes with its conjugate transpose if and only if it is diagonalizable by an orthogonal matric.

嗯。Permutation matrix的inverse就是它的transpose。它也是orthogonal啊。还能被一个orthogonal的matrix对角化。全搞到一起了。

TheMatrix 写了： 2023年 1月 5日 12:58 嗯。Permutation matrix的inverse就是它的transpose。它也是orthogonal啊。还能被一个orthogonal的matrix对角化。全搞到一起了。

一般默认表示矩阵都是unitary矩阵，就是unitary theorem

TheMatrix 写了： 2023年 1月 5日 12:01 我在用permutation character/representation做。群作用在某subgroup coset上。permutation representation群矩阵简单，每行只有一个元素，而且是1。

我在找Symm(5)的6维不可约表示。我找到一个20维的permutation representation，按照character table分解，里面有一个trivial character，两个4维character（不同的），一个5维character，和一个6维的character。

我发现：
1，不管几维的表示，每个元素的eigenvalue都是root of unity，和群元素的阶有关。这个比较好理解。
2，每个矩阵都能完全对角化 - 相似对角化。也就是全部eigenvector span。这个应该也是定理吧？

所以在20维中找6维不可约表示，也就是找6维的公共不可约不变子空间，是一个组合问题。这里有对称性，但比较纷乱。

搞定了。不是用eigenvector组合的方法。而是用character的方法。这两种方法我都在想。eigenvector组合的方法也值得思考，这里有很多组合和对称。但是character的方法，如果能搞定，是更简洁的。我想出来的就是character的方法。

Symm(5)，已知character table，已知有一个6维的不可约表示，已知其character。它的character，就是一个群函数，也就是这个表示空间(regular representation) 中的一个向量。全部群元素乘以这个向量，不能超出这个不可约表示的总维度。但是，regular representation中，6维的不可约表示有6个。所以全部群元素乘以这个character，会span出36维空间，等于6个6维空间的直和。所以还是要在36维空间中找6维的不变子空间。这就是困难所在。

而我用subgroup coset permutation representation，我可以任意选subgroup。得到的representation根据character table算一下，可以知道其中有哪些不可约表示。我选那种只有一个6维不可约表示的。最小的我找到一个20维的subgroup coset permutation representation。这里面有一个1维trivial表示，两个4维character（不同的），一个5维character，和一个6维的character。我就是要在这个20维空间中找到那个独一份的6维不变子空间。

这个地方我非常的满意自己。我想这个character，作为群函数，它是一个120个元素的群上的函数。我现在要找的是一个20个coset上的一个函数。如果能把120元素上的函数somehow restricted到20个coset上，是不是就直接得到我要找的6维不变子空间中的一个向量了呢？最终是成功的。但是120个元素到20个coset之间的关系，应该是什么关系？inclusion？projection？似乎没有canonical的关系。要试验。最后是projection的关系。然后每个coset里的元素的character的值相加。这是我想出的最“自然”的方法。试了一下，果不其然！

所以我就找到了20维表示中的6维不变子空间，也找到了这个不可约表示的matrix表达。

TheMatrix 写了： 2023年 1月 5日 22:35 搞定了。不是用eigenvector组合的方法。而是用character的方法。这两种方法我都在想。eigenvector组合的方法也值得思考，这里有很多组合和对称。但是character的方法，如果能搞定，是更简洁的。我想出来的就是character的方法。

Symm(5)，已知character table，已知有一个6维的不可约表示，已知其character。它的character，就是一个群函数，也就是这个表示空间(regular representation) 中的一个向量。全部群元素乘以这个向量，不能超出这个不可约表示的总维度。但是，regular representation中，6维的不可约表示有6个。所以全部群元素乘以这个character，会span出36维空间，等于6个6维空间的直和。所以还是要在36维空间中找6维的不变子空间。这就是困难所在。

而我用subgroup coset permutation representation，我可以任意选subgroup。得到的representation根据character table算一下，可以知道其中有哪些不可约表示。我选那种只有一个6维不可约表示的。最小的我找到一个20维的subgroup coset permutation representation。这里面有一个1维trivial表示，两个4维character（不同的），一个5维character，和一个6维的character。我就是要在这个20维空间中找到那个独一份的6维不变子空间。

这个地方我非常的满意自己。我想这个character，作为群函数，它是一个120个元素的群上的函数。我现在要找的是一个20个coset上的一个函数。如果能把120元素上的函数somehow restricted到20个coset上，是不是就直接得到我要找的6维不变子空间中的一个向量了呢？最终是成功的。但是120个元素到20个coset之间的关系，应该是什么关系？inclusion？projection？似乎没有canonical的关系。要试验。最后是projection的关系。然后每个coset里的元素的character的值相加。这是我想出的最“自然”的方法。试了一下，果不其然！

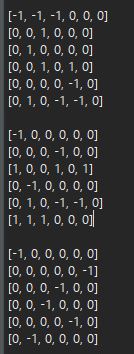
所以我就找到了20维表示中的6维不变子空间，也找到了这个不可约表示的matrix表达。

它长什么样呢？差不多都是这个样子：

TheMatrix 写了： 2023年 1月 5日 22:39 它长什么样呢？差不多都是这个样子：

那个20维表示怎么找到的，正规表示是120维的吧

TheMatrix 写了： 2023年 1月 5日 22:35 搞定了。不是用eigenvector组合的方法。而是用character的方法。这两种方法我都在想。eigenvector组合的方法也值得思考，这里有很多组合和对称。但是character的方法，如果能搞定，是更简洁的。我想出来的就是character的方法。

Symm(5)，已知character table，已知有一个6维的不可约表示，已知其character。它的character，就是一个群函数，也就是这个表示空间(regular representation) 中的一个向量。全部群元素乘以这个向量，不能超出这个不可约表示的总维度。但是，regular representation中，6维的不可约表示有6个。所以全部群元素乘以这个character，会span出36维空间，等于6个6维空间的直和。所以还是要在36维空间中找6维的不变子空间。这就是困难所在。

而我用subgroup coset permutation representation，我可以任意选subgroup。得到的representation根据character table算一下，可以知道其中有哪些不可约表示。我选那种只有一个6维不可约表示的。最小的我找到一个20维的subgroup coset permutation representation。这里面有一个1维trivial表示，两个4维character（不同的），一个5维character，和一个6维的character。我就是要在这个20维空间中找到那个独一份的6维不变子空间。

这个地方我非常的满意自己。我想这个character，作为群函数，它是一个120个元素的群上的函数。我现在要找的是一个20个coset上的一个函数。如果能把120元素上的函数somehow restricted到20个coset上，是不是就直接得到我要找的6维不变子空间中的一个向量了呢？最终是成功的。但是120个元素到20个coset之间的关系，应该是什么关系？inclusion？projection？似乎没有canonical的关系。要试验。最后是projection的关系。然后每个coset里的元素的character的值相加。这是我想出的最“自然”的方法。试了一下，果不其然！

所以我就找到了20维表示中的6维不变子空间，也找到了这个不可约表示的matrix表达。

我没完全看懂（因为我本来就对群表示模模糊糊的），但感觉你这并不是解答“找多个矩阵的共同不变子空间有没有什么经典算法？”，而是解答“给定一个群并给定一个维数，怎么给出一个群表示”。

TheMatrix 写了： 2023年 1月 5日 22:39 它长什么样呢？差不多都是这个样子：

赞！虽然我没看懂。

Caravel 写了： 2023年 1月 5日 23:46 那个20维表示怎么找到的，正规表示是120维的吧

20维的表示是用subgroup coset找到的。取两个元素，生成它们的subgroup，找到subgroup的cosets。群元素也作用在cosets上，是一个permutation of cosets。这个叫permutation representation，因为相当于作用在cosets生成的线性空间上。permutation representation的character很容易计算。然后再用character table算一下其中有哪些不可约表示。我就这样循环找到两个元素，它们的coset permutation representation是20维的，包含1个1维，两个4维，1个5维，1个6维。我的目的是找到一个其中只包含1个6维的。

YWY 写了： 2023年 1月 5日 23:59 我没完全看懂（因为我本来就对群表示模模糊糊的），但感觉你这并不是解答“找多个矩阵的共同不变子空间有没有什么经典算法？”，而是解答“给定一个群并给定一个维数，怎么给出一个群表示”。

你说的对。

我这个是找到群表示空间的一个共同不变子空间。不是对任意的多个矩阵，必须是群表示矩阵。这里有很强的对称性，所以不用general的方法。

如果是general的多个矩阵找共同不变子空间的话，我觉得还得求eigenvalue，eigenspace，若当分解，然后以组合的方法去找。

rgg 写了： 2023年 1月 6日 10:54 赞！虽然我没看懂。

哦。谢谢。这都是早就解决的问题。自己玩玩而已。还得谢谢你那篇不到8页纸的note。字字珠玑啊。

TheMatrix 写了： 2023年 1月 6日 11:28 20维的表示是用subgroup coset找到的。取两个元素，生成它们的subgroup，找到subgroup的cosets。群元素也作用在cosets上，是一个permutation of cosets。这个叫permutation representation，因为相当于作用在cosets生成的线性空间上。permutation representation的character很容易计算。然后再用character table算一下其中有哪些不可约表示。我就这样循环找到两个元素，它们的coset permutation representation是20维的，包含1个1维，两个4维，1个5维，1个6维。我的目的是找到一个其中只包含1个6维的。

哦，和regular representation的思路类似，但是作用在cosets上。这个有点类似商群，2个元素好像有点不够啊？6个元素，cosets的集才能降到20维。

Caravel 写了： 2023年 1月 6日 11:47 哦，和regular representation的思路类似，但是作用在cosets上。这个有点类似商群，2个元素好像有点不够啊？6个元素，cosets的集才能降到20维。

对。regular representation可以看成是trivial subgroup coset representation。我在这两个的关系上想了一段时间，因为希望把character函数从group上迁移到coset上。也没怎么用上。最后用到的就是个简单的相加。

两个元素generate的subgroup。两个元素很容易就generate很大的subgroup，我要的还不能太大，因为coset要20个。

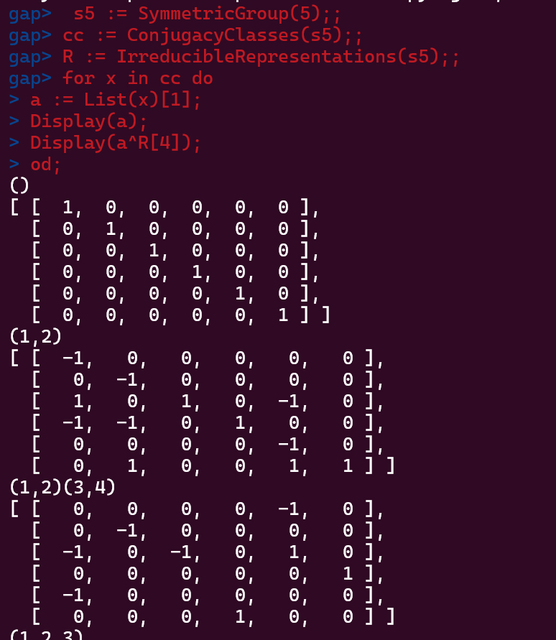
学习一下使用软件GAP：

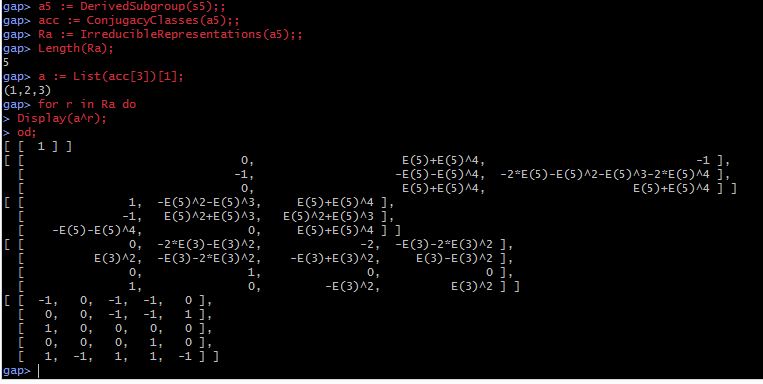
rgg 写了： 2023年 1月 6日 13:46 学习一下使用软件GAP：

不错。我也安装玩了一下。算了一下A5的表示。其中E(3)和E(5)是3次和5次root of unity。

这其中最后一步是怎么弄的我还没有看明白，假设已经找到20维表示了，怎么找到那6维的不变子空间。是直接brute force求解6个基向量么？这样有120个变量，每个群元素的character都知道，有120个方程，好像够了，但是似乎比较慢。

有意思，有空我也来玩玩。