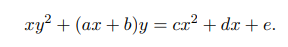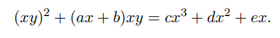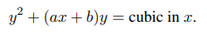椭圆曲线有标准形式:TheMatrix 写了: 2023年 9月 28日 14:13 搭界的东西越来越多,所以就有不同方向的研究 - well,都是研究明白的了 - 也就有不同的展开方式。
直奔主题的话,定义来了:三次方程给出的curve就叫椭圆曲线。注意,叫curve的话,必须首先已经是一个variety,也就是已经是一个方程(组)的zero set。
y2=x3+ax+b
这个叫Weierstrass short form。
还有Weierstrass standard form:
y2+a1xy+a3y = x3+a2x2+a4x+a6
最最一般的三次方程(二元)什么样呢?
y3+c1xy2+c2x2y+c3x3+c4y2+c5xy+c6x2+c7y+c8x+c9=0