分页: 1 / 1
复变函数,帮忙看看,多谢!
发表于 : 2023年 1月 28日 18:09
由 q2014
搞不懂红色框里面的Δz怎么算出来的。

这是我自己算的
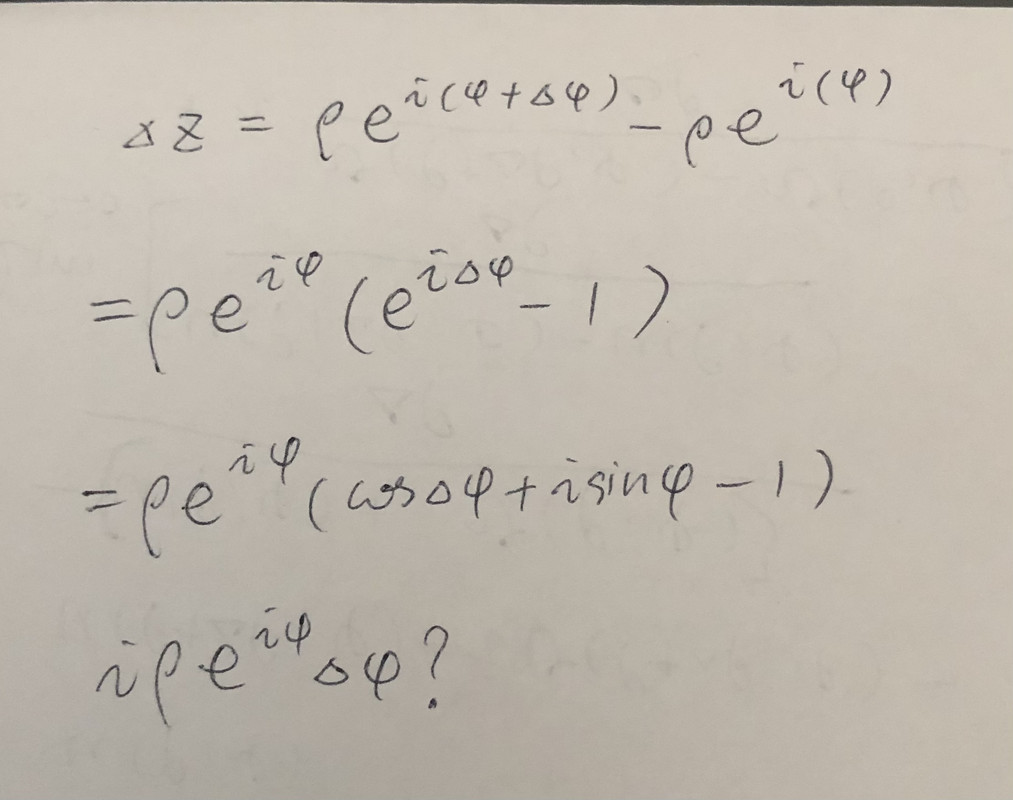
怎么对不上?!
Re: 复变函数,帮忙看看,多谢!
发表于 : 2023年 1月 28日 18:24
由 (ヅ)
q2014 写了: 2023年 1月 28日 18:09
搞不懂红色框里面的Δz怎么算出来的。

这是我自己算的
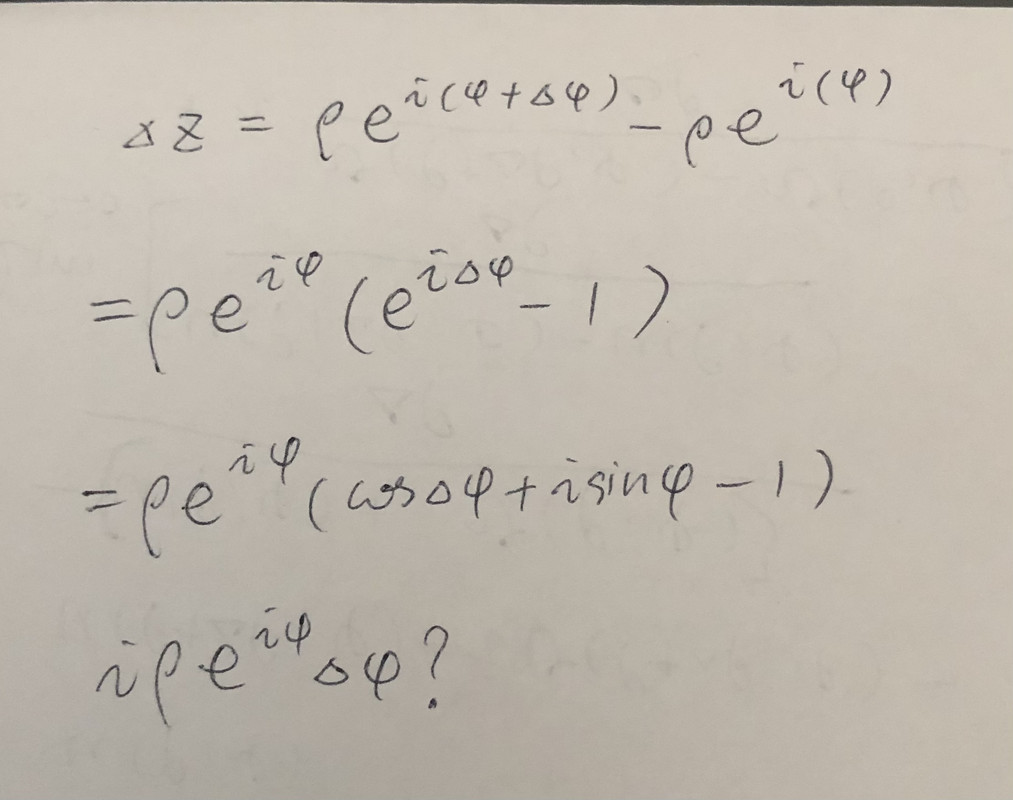
怎么对不上?!
你忘了e^x的taylor series吧
不过也没关系, i*sin(\delta \phi) (这里有个typo)
= i (x- 1/3!* (\delta \phi)^3 + 。。。)
cos(\delta\phi) - 1
= (1- 1/2 *(\delta\phi)^2+1/4! * x^4-\frac{1}{6!}(\delta\phi)^6 + ...) - 1
= - 1/2 *(\delta\phi)^2+1/4! * x^4-\frac{1}{6!}(\delta\phi)^6 + ...
那么cos(\delta \phi) + isin(\delta \phi) - 1
= i(\delta \phi) + O((\delta \phi)^2)
\approx i(\delta \phi)
你求导数偏导数的时候,只有(\delta \phi)的一次项留下来了,剩下的都是
\lim_(\delta\phi \to 0) O((\delta \phi)^2) / (\delta \phi) = 0
Re: 复变函数,帮忙看看,多谢!
发表于 : 2023年 1月 28日 18:39
由 YWY
套公式的话,就是把rho当常数算e^{i phi}对phi的微分。
你图里在草纸上试图自己推导(不套公式),也不是不行。画图的话能看出当 delta phi无穷小时,cos(delta phi) + i sin(delta phi) - 1趋于1 + i sin(delta phi) - 1 = i sin(delta phi) 趋于 i delta phi,这样就出来了。
Re: 复变函数,帮忙看看,多谢!
发表于 : 2023年 1月 28日 19:18
由 Caravel
(ヅ) 写了: 2023年 1月 28日 18:24
你忘了e^x的taylor series吧
不过也没关系, i*sin(\delta \phi) (这里有个typo)
= i (x- 1/3!* (\delta \phi)^3 + 。。。)
cos(\delta\phi) - 1
= (1- 1/2 *(\delta\phi)^2+1/4! * x^4-\frac{1}{6!}(\delta\phi)^6 + ...) - 1
= - 1/2 *(\delta\phi)^2+1/4! * x^4-\frac{1}{6!}(\delta\phi)^6 + ...
那么cos(\delta \phi) + isin(\delta \phi) - 1
= i(\delta \phi) + O((\delta \phi)^2)
\approx i(\delta \phi)
你求导数偏导数的时候,只有(\delta \phi)的一次项留下来了,剩下的都是. 写完发现上面也有人说了
\lim_(\delta\phi \to 0) O((\delta \phi)^2) / (\delta \phi) = 0
cos x , sin x, 展开一下就知道了,一阶近似 cosx 等于1 , sinx 等于 x, 或者你对phi 求导也是一样的结果
Re: 复变函数,帮忙看看,多谢!
发表于 : 2023年 1月 28日 19:23
由 Amorphous
泰勒展开
Re: 复变函数,帮忙看看,多谢!
发表于 : 2023年 1月 29日 11:47
由 q2014
解释的非常清楚,多谢各位!