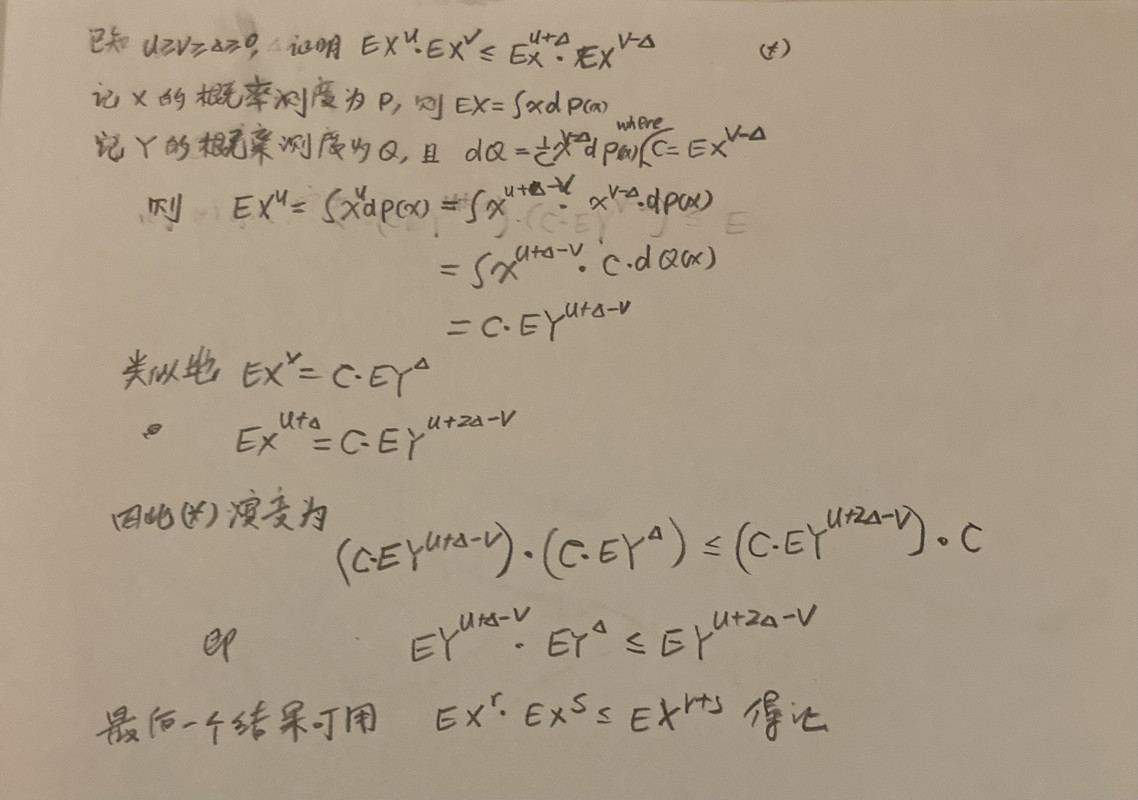分页: 1 / 2
#1 概率题:E[X^i]E[X^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 16日 16:57
由 FoxMe
E[Xi]E[Xj] <= E[Xi+j]成立吗?这里随机变量X>0,i,j是正整数。
#2 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 16日 19:08
由 TheMatrix
FoxMe 写了: 2023年 11月 16日 16:57
E[X
i]E[
j] <= E[X
i+j]成立吗?这里随机变量X>0,i,j是正整数。
方向反了吧?应该是大于等于。
#3 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 16日 19:27
由 nk
FoxMe 写了: 2023年 11月 16日 16:57
E[X
i]E[
j] <= E[X
i+j]成立吗?这里随机变量X>0,i,j是正整数。
这个很好证的, 利用Holder 不等式,得到蓝线的东西,然后用 s=i +j, 然后设 r=i 和 r=j 就可以了

#4 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 16日 19:27
由 nk
TheMatrix 写了: 2023年 11月 16日 19:08
方向反了吧?应该是大于等于。
方向没有错
#5 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 16日 19:28
由 GreatCanada
TheMatrix 写了: 2023年 11月 16日 19:08
方向反了吧?应该是大于等于。
方向没有反,好像可以由赫尔德不等式证明,怎么证忘了
#6 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 16日 21:44
由 TheMatrix
newkids_on_the_block 写了: 2023年 11月 16日 19:27
这个很好证的, 利用Holder 不等式,得到蓝线的东西,然后用 s=i +j, 然后设 r=i 和 r=j 就可以了

确实。
我出一个相关的题:
还是假设X为正随机变量,(p,q)为Holder conjugate,假设p<q。
如果有另一对Holder conjugate (p',q'),p'<q'的话,
那么 p'<=p ==> E(X
1/p)E(X
1/q) <= E(X
1/p')E(X
1/q')。
#7 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 16日 21:56
由 TheMatrix
TheMatrix 写了: 2023年 11月 16日 21:44
确实。
我出一个相关的题:
还是假设X为正随机变量,(p,q)为Holder conjugate,假设p<q。
如果有另一对Holder conjugate (p',q'),p'<q'的话,
那么 p'<=p ==> E(X
1/p)E(X
1/q) <= E(X
1/p')E(X
1/q')。
我这么改一下吧:
假设q>=2,假设p为q的Holder conjugate,即 1/p+1/q=1。
对于任意正随机变量X,定义K(X,q)=E(X
1/p)E(X
1/q),
那么K(X,q)是q的单调递增函数。
#9 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 17日 12:09
由 TheMatrix
TheMatrix 写了: 2023年 11月 16日 21:56
我这么改一下吧:
假设q>=2,假设p为q的Holder conjugate,即 1/p+1/q=1。
对于任意正随机变量X,定义K(X,q)=E(X
1/p)E(X
1/q),
那么K(X,q)是q的单调递增函数。
这个问题引入Holder conjugate有点多余。应该直接这么说:
有两个正数相加等于1:u+v=1。
定义K(X,u)=E(X
u)E(X
v)。
那么,K(X,u)随着u和v之间的距离|u-v|而变化 - 单调递增。
最小的是当u=v=1/2。这时有 E(X
1/2) <= E(X)
1/2。
最大的是当u=0,v=1。这时有 E(X
u)E(X
v) <= E(X)。这基本上就是原问题。
#10 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 17日 13:19
由 FoxMe
赞!
Jensen不等式很厉害,可以不用Holder不等式:如果r<s,则x
r/s凸,那么E[X
r/s]<=E[X]
r/s. 把X改成X
s就得到蓝线里的公式。
newkids_on_the_block 写了: 2023年 11月 16日 19:27
这个很好证的, 利用Holder 不等式,得到蓝线的东西,然后用 s=i +j, 然后设 r=i 和 r=j 就可以了

#11 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 18日 22:38
由 TheMatrix
TheMatrix 写了: 2023年 11月 17日 12:09
这个问题引入Holder conjugate有点多余。应该直接这么说:
有两个正数相加等于1:u+v=1。
定义K(X,u)=E(X
u)E(X
v)。
那么,K(X,u)随着u和v之间的距离|u-v|而变化 - 单调递增。
最小的是当u=v=1/2。这时有 E(X
1/2) <= E(X)
1/2。
最大的是当u=0,v=1。这时有 E(X
u)E(X
v) <= E(X)。这基本上就是原问题。
这个小问题首先应该是对的。证明应该也是比较简单的。但是我还没有找到一个简单的证明。
简单的证明应该是用Jensen 或者 Holder,用上这两个的,一般都很简单,但是很巧妙。
这样的定理数学中有不少,小而硬核,缺了就不行。比如。。。我刚想到一个,一下就忘了。
我又看了一下Jensen 和 Holder,这两个有明显的区别:Jensen是一个函数,而Holder是两个函数相乘。把这两个定理联系到一起,也是非常非常不显而易见的。
#12 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 19日 08:17
由 nk
TheMatrix 写了: 2023年 11月 17日 12:09
这个问题引入Holder conjugate有点多余。应该直接这么说:
有两个正数相加等于1:u+v=1。
定义K(X,u)=E(X
u)E(X
v)。
那么,K(X,u)随着u和v之间的距离|u-v|而变化 - 单调递增。
最小的是当u=v=1/2。这时有 E(X
1/2) <= E(X)
1/2。
最大的是当u=0,v=1。这时有 E(X
u)E(X
v) <= E(X)。这基本上就是原问题。
这个结果有可能是对的,花了几分钟想了一下无果,就放弃了哈。如果有人有答案,不管是简单的还是复杂的,请分享一下。
#13 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 19日 11:58
由 TheMatrix
TheMatrix 写了: 2023年 11月 17日 12:09
这个问题引入Holder conjugate有点多余。应该直接这么说:
有两个正数相加等于1:u+v=1。
定义K(X,u)=E(X
u)E(X
v)。
那么,K(X,u)随着u和v之间的距离|u-v|而变化 - 单调递增。
最小的是当u=v=1/2。这时有 E(X
1/2) <= E(X)
1/2。
最大的是当u=0,v=1。这时有 E(X
u)E(X
v) <= E(X)。这基本上就是原问题。
newkids_on_the_block 写了: 2023年 11月 19日 08:17
这个结果有可能是对的,花了几分钟想了一下无果,就放弃了哈。如果有人有答案,不管是简单的还是复杂的,请分享一下。
我是这么“说明”的:
1,为了比较两对(u,v)对结果的影响,取(u,v),(u',v')都为有理数。一般实数的话,打算用continuity argment。
2,找到全部数的common denominator,clear denominator,把4个数都变成正整数,而且有u+v=u'+v'=k。u<=v,u'<=v',u'<=u,也就是(u',v')之间的距离比(u,v)大。要证明(u',v')得到的结果也比(u,v)大。
3,随机变量X的话,在概率空间上细分,使每个小块的概率相同,并且X在其上的取值“接近”常数。然后打算用极限的argument。
4,两对正整数(u,v)和(u',v'),进一步假设相差仅为1:u=u'+1,对应的v'=v+1。相差不为1的话,证明方式是相同的。
5,随机变量细分,再进一步假设只有两块,每块概率相同,X的取值为a和b。很多块的话,希望用summation notation证明。
6,最后化简的问题就变成,证明:
(a
u+b
u)(a
v+b
v) <= (a
(u-1)+b
(u-1))(a
(v+1)+b
(v+1))
这个比较容易证明。
#14 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 19日 14:23
由 nk
TheMatrix 写了: 2023年 11月 19日 11:58
我是这么“说明”的:
1,为了比较两对(u,v)对结果的影响,取(u,v),(u',v')都为有理数。一般实数的话,打算用continuity argment。
2,找到全部数的common denominator,clear denominator,把4个数都变成正整数,而且有u+v=u'+v'=k。u<=v,u'<=v',u'<=u,也就是(u',v')之间的距离比(u,v)大。要证明(u',v')得到的结果也比(u,v)大。
3,随机变量X的话,在概率空间上细分,使每个小块的概率相同,并且X在其上的取值“接近”常数。然后打算用极限的argument。
4,两对正整数(u,v)和(u',v'),进一步假设相差仅为1:u=u'+1,对应的v'=v+1。相差不为1的话,证明方式是相同的。
5,随机变量细分,再进一步假设只有两块,每块概率相同,X的取值为a和b。很多块的话,希望用summation notation证明。
6,最后化简的问题就变成,证明:
(a
u+b
u)(a
v+b
v) <= (a
(u-1)+b
(u-1))(a
(v+1)+b
(v+1))
这个比较容易证明。
你的很多简化步骤好像已经和原题差得太远了一些。也许从这个想法能够推导出严格的证明。我没有花时间去想。
我自己的想法是 考虑 delta 方法,把 u 增加到 u+d, d是一个非常小的数,会对E(X
u)E(X
v) 产生什么影响。
但是没有演算出来,也不知道这一条道可不可行。
#15 Re: 概率题:E[X^i]E[^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 19日 15:22
由 TheMatrix
newkids_on_the_block 写了: 2023年 11月 19日 14:23
你的很多简化步骤好像已经和原题差得太远了一些。也许从这个想法能够推导出严格的证明。我没有花时间去想。
我自己的想法是 考虑 delta 方法,把 u 增加到 u+d, d是一个非常小的数,会对E(X
u)E(X
v) 产生什么影响。
但是没有演算出来,也不知道这一条道可不可行。
嗯。你这个思路是直接的,也是这个问题的目的。
如果能用上Jensen,Holder,或者Young's的话,应该会简单很多。
#16 Re: 概率题:E[X^i]E[X^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 19日 17:51
由 FoxMe
赞二位的专研精神,这个推广很有意思。考虑以下情况就差不多了:
E[X2]E[X2] <= E[X3]E[X1] <= E[X4]是否成立?
#17 Re: 概率题:E[X^i]E[X^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 19日 19:13
由 TheMatrix
FoxMe 写了: 2023年 11月 19日 17:51
赞二位的专研精神,这个推广很有意思。考虑以下情况就差不多了:
E[X
2]E[X
2] <= E[X
3]E[X
1] <= E[X
4]是否成立?
对。就是这个情况。下面这个更好,中间的两个:
E[X
3]E[X
3] <= E[X
2]E[X
4] <= E[X
1]E[X
5] <= E[X
6]
#18 Re: 概率题:E[X^i]E[X^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 20日 06:25
由 nk
TheMatrix 写了: 2023年 11月 19日 15:22
嗯。你这个思路是直接的,也是这个问题的目的。
如果能用上Jensen,Holder,或者Young's的话,应该会简单很多。
FoxMe 写了: 2023年 11月 19日 17:51
赞二位的专研精神,这个推广很有意思。考虑以下情况就差不多了:
E[X
2]E[X
2] <= E[X
3]E[X
1] <= E[X
4]是否成立?
居然还是想出来了。很多年没有动这些方面的东西了,年轻时应该是容易的题目。
不懂概率测度的ID,就用概率密度函数做,思路完全一样的
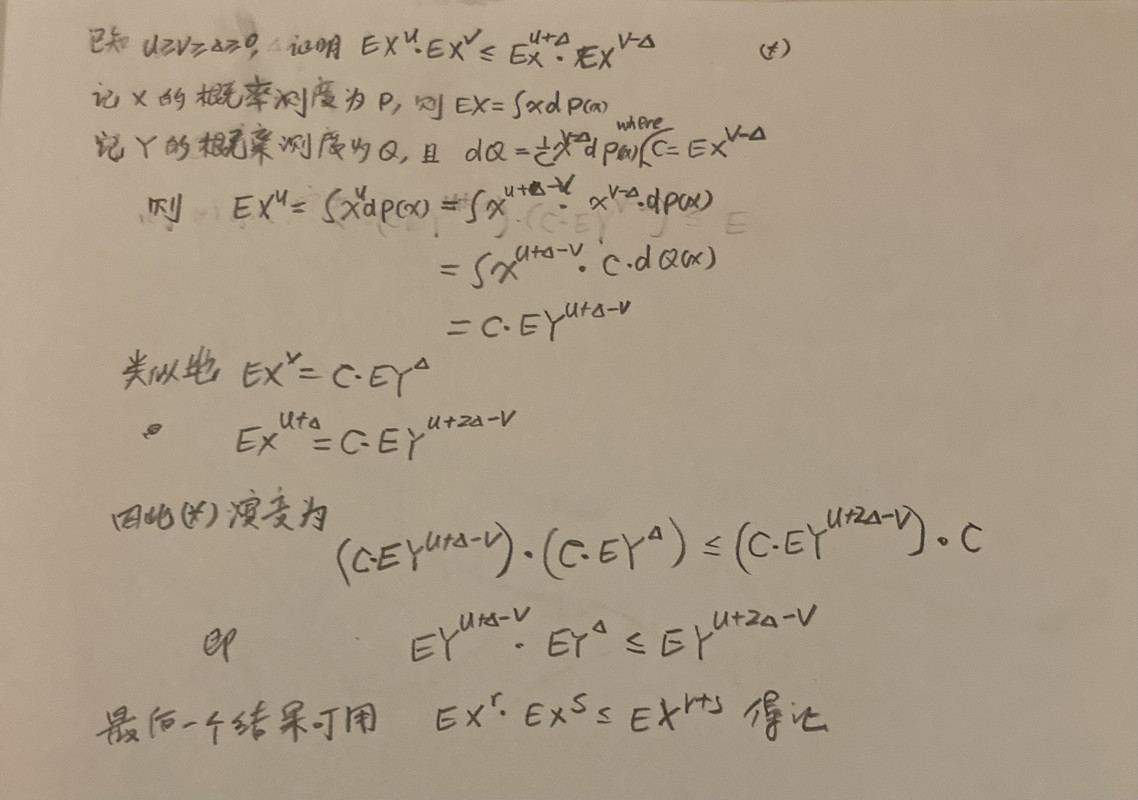
#19 Re: 概率题:E[X^i]E[X^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 20日 11:35
由 TheMatrix
newkids_on_the_block 写了: 2023年 11月 20日 06:25
居然还是想出来了。很多年没有动这些方面的东西了,年轻时应该是容易的题目。
不懂概率测度的ID,就用概率密度函数做,思路完全一样的
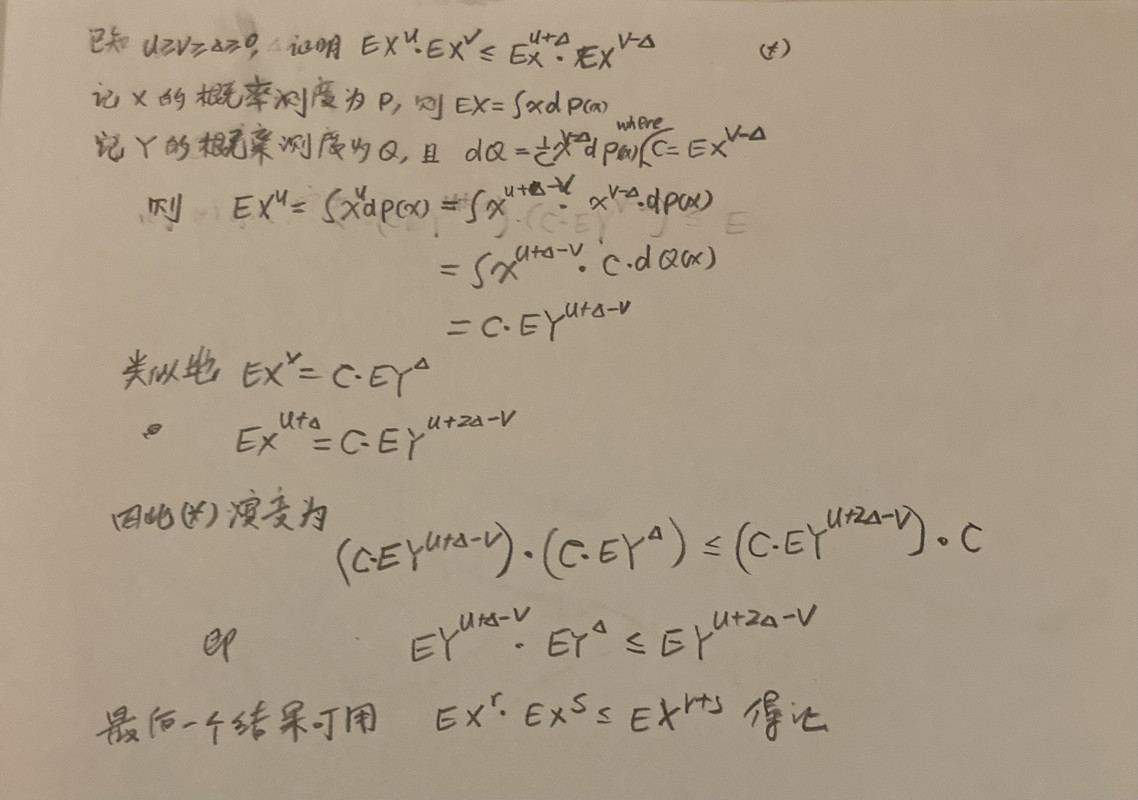
嗯。很好!
还是归结到E[X^i]E[X^j] <= E[X^(i+j)]的形式。换measure的处理有点像证明Holder不等式。
#20 Re: 概率题:E[X^i]E[X^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 20日 13:48
由 FoxMe
赞!我也看到一个证明,用logE(x
t)的凹性:
https://www.researchgate.net/publicatio ... _variables
For a nonnegative random variable X, the Sclove et al. inequality [38, (5)] is
E X
r+1 E X
s−1 <= E X
r E X
s, 0 <= r <= s − 1.
引用的是196几年的文章。
#21 Re: 概率题:E[X^i]E[X^j] <= E[X^(i+j)]成立吗
发表于 : 2023年 11月 20日 16:30
由 nk
也提到了Olkin 2006 的结果,就和我的描述是一模一样的。说起来我还邀请他做过报告的和他一起吃饭的,哈哈。
那个年轻时做概率统计的经历太久远了。