出个和黎曼猜想相关的题

[TheMatrix]

黎曼zeta函数：zeta(s) = Σ n^-s

令 s = x + iy，其中x,y为实数。

众所周知，当x>1的时候，该级数绝对收敛。

问：当0<x<=1的时候，该级数是否收敛。

注意：这个问题不同于zeta函数的解析延拓 - 众所周知，zeta函数可以解析延拓到整个复平面上。而这个问题问的是级数本身是否收敛。

[TheMatrix]

首先，当x<=0的时候，该级数肯定是不收敛的。因为一个级数 Σ a_n 收敛的必要条件是 a_n --> 0。而当x<=0时，n^-s不趋近于0。

[TheMatrix]

n^-s = n^-xn^-iy

而n^-iy = e^-iθ，where θ = y ln(n)，这是一个纯角度旋转。

而n^-x是该项的长度。当x<=1的时候，长度绝对和是不收敛的。

我本来以为每一项的角度旋转可以使该级数收敛，就好像alternating级数互相cancel的效果一样。但是看来可能并不如此。

[TheMatrix]

n^-s = n^-xn^-iy

而n^-iy = e^-iθ，where θ = y ln(n)，这是一个纯角度旋转。

而n^-x是该项的长度。当x<=1的时候，长度绝对和是不收敛的。

我本来以为每一项的角度旋转可以使该级数收敛，就好像alternating级数互相cancel的效果一样。但是看来可能并不如此。

下图是 s=x+iy在各种情况下的级数增长图。取2000项。

可以看到 x>1 的时候级数绝对收敛，所以总长度有限。

0<x<1的时候，比如x=0.5，总长度是趋于无穷的，而角度的变化并不产生cancel的效果，所以是螺旋扩大的曲线，看起来是不收敛的。

x=1的时候，总长度是调和级数，也是不收敛的。角度的旋转恰好和长度相配合，所以看起来是在圆周上旋转。级数总体来看，应该也是不收敛的。

不知道怎么证明。

s = 1.5 + 3i


s = 0.5 + 3i


s = 1 + 3i

[TheMatrix]

下图是 s=x+iy在各种情况下的级数增长图。取2000项。

可以看到 x>1 的时候级数绝对收敛，所以总长度有限。

0<x<1的时候，比如x=0.5，总长度是趋于无穷的，而角度的变化并不产生cancel的效果，所以是螺旋扩大的曲线，看起来是不收敛的。

x=1的时候，总长度是调和级数，也是不收敛的。角度的旋转恰好和长度相配合，所以看起来是在圆周上旋转。级数总体来看，应该也是不收敛的。

不知道怎么证明。

s = 1.5 + 3i


s = 0.5 + 3i


s = 1 + 3i

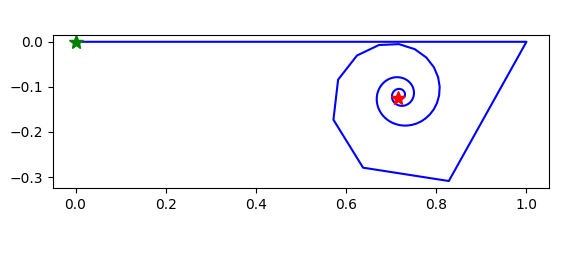
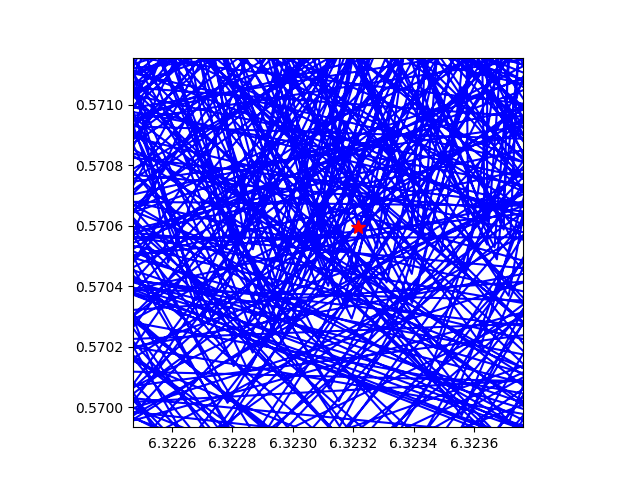
这个图也是很有意思的。

比如看 s = 0.5 + 3i的情况。每一项的长度 n^-0.5 = 1/√n。而每一项和上一项相比，转动的角度是 ln(n)-ln(n-1) ≈ 1/n，比长度的增量要小。所以长度的增量无处安放，只能是螺旋向外扩展。所以该级数不收敛。

这是一个形象化说明。我觉得应该可以据此形成一个证明。

[TheMatrix]

这个图也是很有意思的。

比如看 s = 0.5 + 3i的情况。每一项的长度 n^-0.5 = 1/√n。而每一项和上一项相比，转动的角度是 ln(n)-ln(n-1) ≈ 1/n，比长度的增量要小。所以长度的增量无处安放，只能是螺旋向外扩展。所以该级数不收敛。

这是一个形象化说明。我觉得应该可以据此形成一个证明。

zeta级数在critical strip (0<=x<=1)上不收敛，那么zeta函数的定义就只能依赖解析延拓了。

[randomatrices]

谢谢你问这个问题。我曾经也想在这问同样的问题，当时我不清楚的是 x=1, y /= 0时这个级数是否收敛。
因为一般的介绍黎曼zeta函数对应的Dirichlet's 级数时， 都会说， 当 x >1 时， 该Dirichlet's 级数收敛， 当 x < 1 时，该Dirichlet's 级数发散。但很少有介绍会说 x = 1 的情形， 当然我们都知道 x = 1 时， 对于 y = 0 的情形， 级数是趋向于无穷大的，但对于 x = 1, y /= 0的情形下，几乎没有关于黎曼zeta函数的书会提到， 大概是和在 line of abscissa上没有普遍适用的判别方法相关。

不过我检索了一下文献， 发现Hardy在他的 Dirichlet's series 书上有提到这个问题， 顺藤摸瓜， 也发现了Bromwich的证明。不过我还没有完整的研究完这个证明 ， 看上去是很有趣的证明。
https://sci-hub.se/https://doi.org/10.1 ... s2-6.1.327

黎曼zeta函数：zeta(s) = Σ n^-s

令 s = x + iy，其中x,y为实数。

众所周知，当x>1的时候，该级数绝对收敛。

问：当0<x<=1的时候，该级数是否收敛。

注意：这个问题不同于zeta函数的解析延拓 - 众所周知，zeta函数可以解析延拓到整个复平面上。而这个问题问的是级数本身是否收敛。

[FoxMe]

一般书上只讨论绝对收敛的情况，没见过其它情况。

[TheMatrix]

谢谢你问这个问题。我曾经也想在这问同样的问题，当时我不清楚的是 x=1, y /= 0时这个级数是否收敛。
因为一般的介绍黎曼zeta函数对应的Dirichlet's 级数时， 都会说， 当 x >1 时， 该Dirichlet's 级数收敛， 当 x < 1 时，该Dirichlet's 级数发散。但很少有介绍会说 x = 1 的情形， 当然我们都知道 x = 1 时， 对于 y = 0 的情形， 级数是趋向于无穷大的，但对于 x = 1, y /= 0的情形下，几乎没有关于黎曼zeta函数的书会提到， 大概是和在 line of abscissa上没有普遍适用的判别方法相关。

不过我检索了一下文献， 发现Hardy在他的 Dirichlet's series 书上有提到这个问题， 顺藤摸瓜， 也发现了Bromwich的证明。不过我还没有完整的研究完这个证明 ， 看上去是很有趣的证明。
https://sci-hub.se/https://doi.org/10.1 ... s2-6.1.327

嗯。关于x=1的情况，结论就是zeta级数在一个圆周上旋转，所以不收敛。

不错。你这个文献好。

研究级数是很困难的，因为级数自带无穷，本质上就是一个无穷维空间。

无穷维空间很难研究，没有系统性穷尽的办法，只能靠洞见。

不过自然界出现的问题，都是无穷的。

不过这里我又看到了combinatorics。复指数级数相当于把两个级数编织在一起，一个负责长度，一个负责角度。角度级数中，本质上还是用了combinatorics的方法 - 我指的是这篇paper靠近结尾处，对角度在周期内变化的讨论。

[TheMatrix]

这个图也是很有意思的。

比如看 s = 0.5 + 3i的情况。每一项的长度 n^-0.5 = 1/√n。而每一项和上一项相比，转动的角度是 ln(n)-ln(n-1) ≈ 1/n，比长度的增量要小。所以长度的增量无处安放，只能是螺旋向外扩展。所以该级数不收敛。

这是一个形象化说明。我觉得应该可以据此形成一个证明。

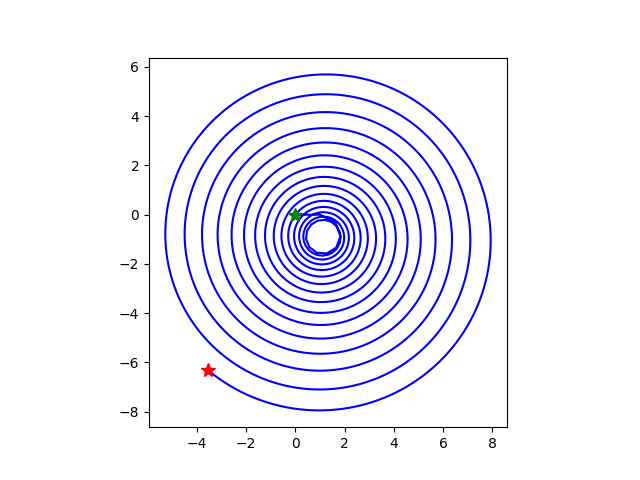
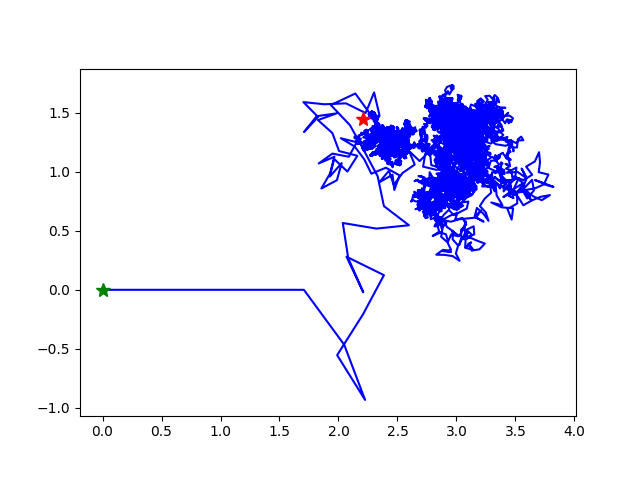
又做了几个有趣的图。

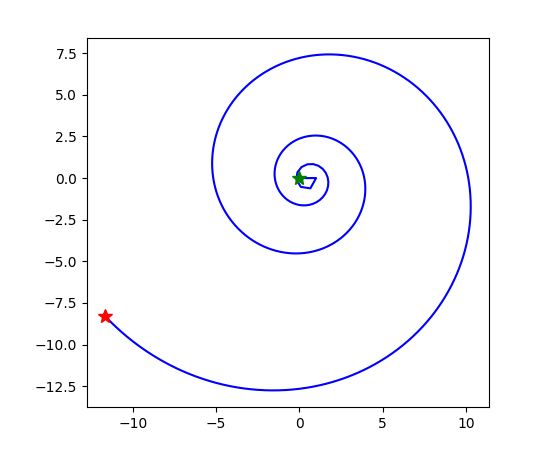
zeta级数 Σ n^-s 的每一项 n^-s=n^-xn^-iy 包含一个长度项n^-x和一个角度项n^-iy=e^{-iy ln(n)}。当x=0.5时，长度项之和不收敛，也就是这个级数的部分和画出的曲线会越来越长。但是它怎么发展要看角度项的变化。

设y=1。我把角度项中的ln(n)变成 ln(n)^k，就是让角度项的变化幅度稍微大一些。看看效果：

取20000项部分和。

k=2，还是螺旋向外扩展的曲线：


k=3，这个还是螺旋向外扩展，但是扩展的很慢了：


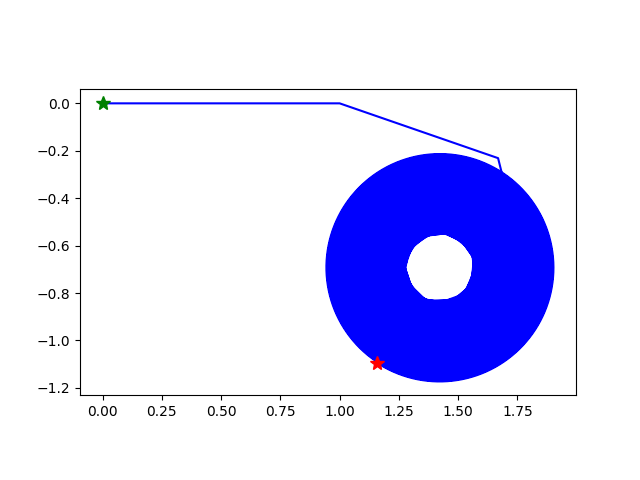
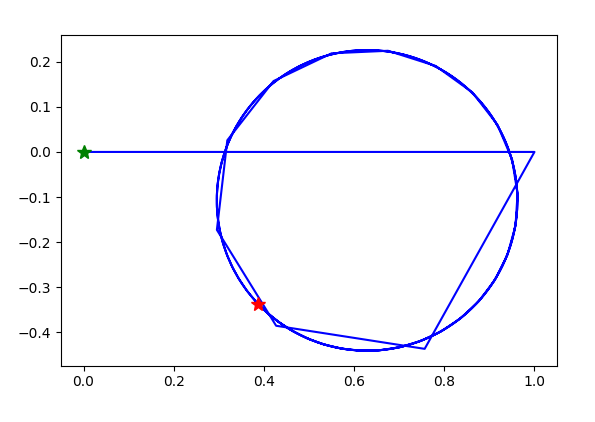
k=4，现在是螺旋向内了！


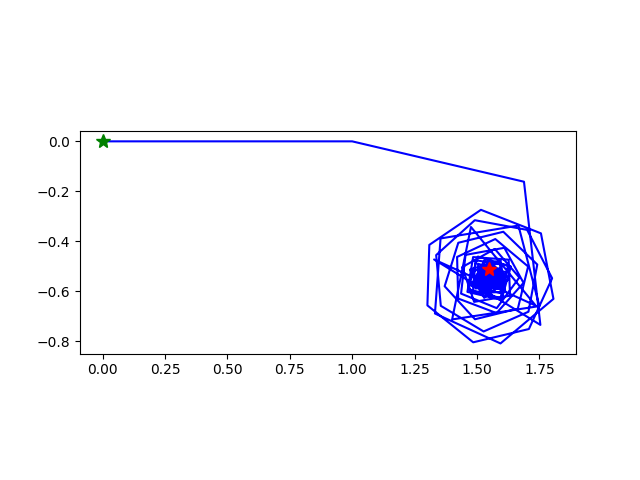
k=5，这个花样很好看。现在看出，虽然是螺旋向内，但是因为长度增长无界，所以一个螺旋满了会跳到另一个螺旋：


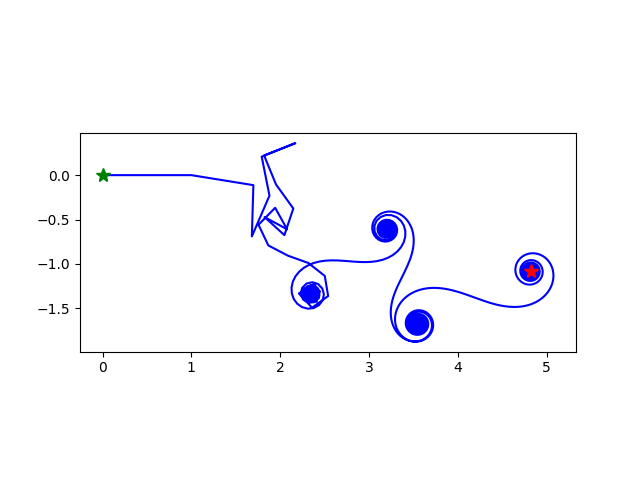
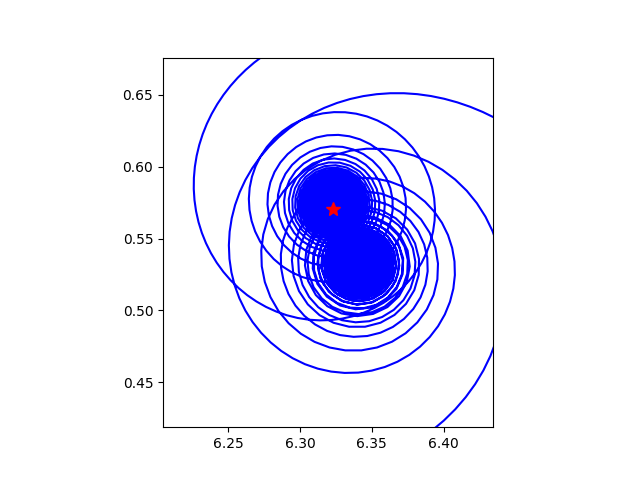
k=6，这个有点奇怪了，最后的点（红色marker）好像不在最后一个螺旋里：


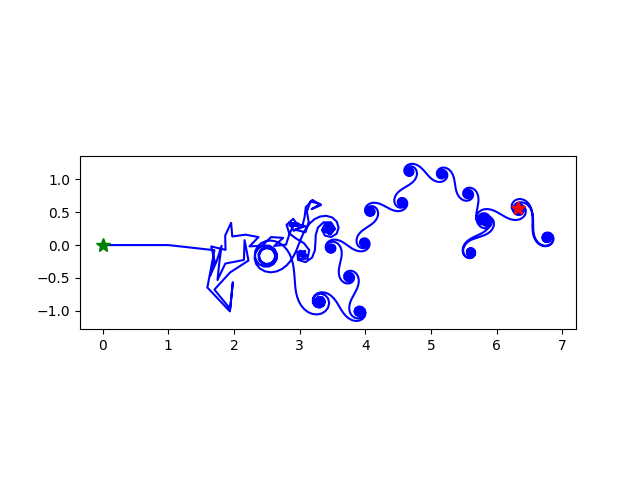
k=7，


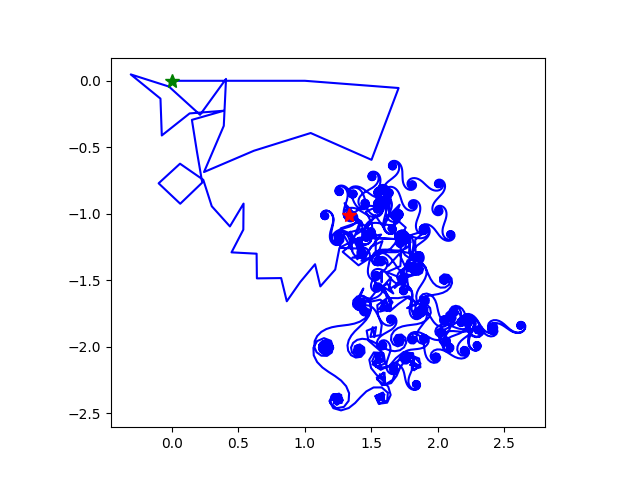
k=8，


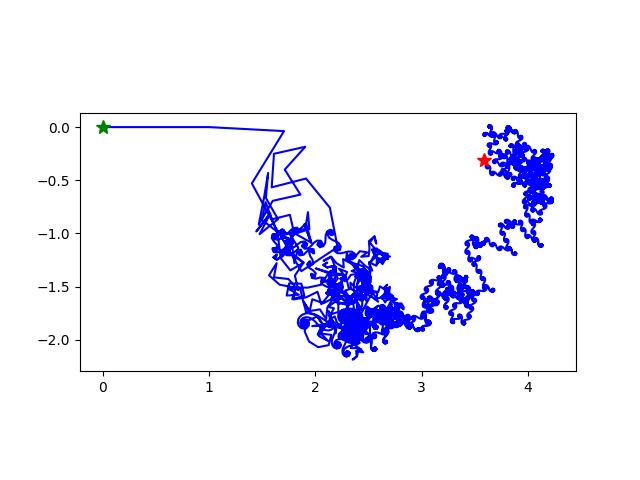
k=100，

[（ヅ）]

s=1为调和级数

[TheMatrix]

k=6，这个有点奇怪了，最后的点（红色marker）好像不在最后一个螺旋里：

k=6放大来看，原来是两个螺旋有点重合：





放大到这么大应该没什么意义了，电脑误差可能已经超过图形精度了：

[changbaihou]

In most courses on analytic number theory, analytic continuation of zeta(s) is one of the first topics covered. Of all the different ways to extend zeta(s) (the series that holds from Re(s) > 1), one classical method is via Euler-Maclaurin summation. Through its simplest form (the Abelian summation formula), you can analytically extend zeta(s) to Re(s)>0 and find that the partial sum \sum{n\leq N}n^{-s} is unbounded (N\to\infty) when 0<Re(s)<1. When s=1+it (t/ne 0), the partial sum is bounded (in terms of t), but does not approach any limit. Therefore, the series \sum{n=1}^{\infty}n^{-s} converges if and only if Re(s)>1.

[TheMatrix]

In most courses on analytic number theory, analytic continuation of zeta(s) is one of the first topics covered. Of all the different ways to extend zeta(s) (the series that holds from Re(s) > 1), one classical method is via Euler-Maclaurin summation. Through its simplest form (the Abelian summation formula), you can analytically extend zeta(s) to Re(s)>0 and find that the partial sum \sum{n\leq N}n^{-s} is unbounded (N\to\infty) when 0<Re(s)<1. When s=1+it (t/ne 0), the partial sum is bounded (in terms of t), but does not approach any limit. Therefore, the series \sum{n=1}^{\infty}n^{-s} converges if and only if Re(s)>1.

嗯，看了一下wiki。这个以积分来估算级数的方法还是很自然的。

wiki上看到一个zeta reciprocal的公式，和zeta本身的公式很相似。有没有巧妙的证明方法？

[pinfish]

这几个图有点混沌的味道...

又做了几个有趣的图。

zeta级数 Σ n^-s 的每一项 n^-s=n^-xn^-iy 包含一个长度项n^-x和一个角度项n^-iy=e^{-iy ln(n)}。当x=0.5时，长度项之和不收敛，也就是这个级数的部分和画出的曲线会越来越长。但是它怎么发展要看角度项的变化。

设y=1。我把角度项中的ln(n)变成 ln(n)^k，就是让角度项的变化幅度稍微大一些。看看效果：

取20000项部分和。

k=2，还是螺旋向外扩展的曲线：


k=3，这个还是螺旋向外扩展，但是扩展的很慢了：


k=4，现在是螺旋向内了！


k=5，这个花样很好看。现在看出，虽然是螺旋向内，但是因为长度增长无界，所以一个螺旋满了会跳到另一个螺旋：


k=6，这个有点奇怪了，最后的点（红色marker）好像不在最后一个螺旋里：


k=7，


k=8，


k=100，

[changbaihou]

嗯，看了一下wiki。这个以积分来估算级数的方法还是很自然的。

wiki上看到一个zeta reciprocal的公式，和zeta本身的公式很相似。有没有巧妙的证明方法？

When Re(s)>1, we have

(\sum_{n=1}^{\infty}1/n^s)(\sum_{m=1}^{\infty}\mu(m)/m^s)=\sum_{m, n=1}^{\infty}\mu(m)/(mn)^s=\sum_{k=1}^{\infty}a(k)/k^s

where a(k)=\sum_{m|k}\mu(k) which is equal to 1 only if k=1, and 0 for k>1. Thus (\sum_{n=1}^{\infty}1/n^s)(\sum_{m=1}^{\infty}\mu(m)/m^s)=1, and so \sum_{m=1}^{\infty}\mu(m)/m^s=1/\zeta(s).

Apparently, a(1)=1, and a(p^h)=\mu(1)+\mu(p)+...+\mu(p^h)=1-1+0+...+0=0 if p is a prime and h\geq 1. The fact that a(k)=0 for k>1 is a result from elementary number theory. For any arithmetic function f, g(n):=\sum_{d|n}f(d) is multiplicative. So a(k) is multiplicative. Let k={p_1}^{\alpha_1}...{p_s}^{\alpha_s} be the prime factorization of k, then a(k)=a(p_1^{\alpha_1})... a(p_s^{\alpha_s}), which is zero if s>0 (ie, k>1).

[TheMatrix]

When Re(s)>1, we have

(\sum_{n=1}^{\infty}1/n^s)(\sum_{m=1}^{\infty}\mu(m)/m^s)=\sum_{m, n=1}^{\infty}\mu(m)/(mn)^s=\sum_{k=1}^{\infty}a(k)/k^s

where a(k)=\sum_{m|k}\mu(k) which is equal to 1 only if k=1, and 0 for k>1. Thus (\sum_{n=1}^{\infty}1/n^s)(\sum_{m=1}^{\infty}\mu(m)/m^s)=1, and so \sum_{m=1}^{\infty}\mu(m)/m^s=1/\zeta(s).

Apparently, a(1)=1, and a(p^h)=\mu(1)+\mu(p)+...+\mu(p^h)=1-1+0+...+0=0 if p is a prime and h\geq 1. The fact that a(k)=0 for k>1 is a result from elementary number theory. For any arithmetic function f, g(n):=\sum_{d|n}f(d) is multiplicative. So a(k) is multiplicative. Let k={p_1}^{\alpha_1}...{p_s}^{\alpha_s} be the prime factorization of k, then a(k)=a(p_1^{\alpha_1})... a(p_s^{\alpha_s}), which is zero if s>0 (ie, k>1).

漂亮。

这个证明也不trivial啊。

给你转一下latex。

[changbaihou]

漂亮。

这个证明也不trivial啊。

给你转一下latex。

That looks so much better. BTW, in my last post, "For any arithmetic function f" should be "For any multiplicative arithmetic function f". Of course you can get around the result I quoted if you notice that, for k={p_1}^{\alpha_1}...{p_s}^{\alpha_s}, the summation in

a(k)=\sum_{d|k}\mu(d)

is actually over square-free divisors of k and thus

a(k)=(\mu(1)+\mu(p_1)...((\mu(1)+\mu(p_s))=0 unless s>0 because of the multiplicity of \mu.

[TheMatrix]

黎曼zeta函数：zeta(s) = Σ n^-s

令 s = x + iy，其中x,y为实数。

众所周知，当x>1的时候，该级数绝对收敛。

问：当0<x<=1的时候，该级数是否收敛。

注意：这个问题不同于zeta函数的解析延拓 - 众所周知，zeta函数可以解析延拓到整个复平面上。而这个问题问的是级数本身是否收敛。

来总结一下和zeta函数有关的方法 - 这些就是黎曼猜想的抓手：
1，zeta级数的定义。
2，积分定义。
3，解析延拓到全平面。
4，functional equation，zeta(s) ~ zeta(1-s)
5，Euler product

没了。我大放厥词了。请大能有以教我。

这就是为什么zeta函数特别的难。因为它没有抓手。可以说特别贫瘠。

接下来大家就开始使出浑身解数，想要硬给它安装抓手：
1，Dirichlet character modulated zeta series。Σ Χ(n)n^-s，也叫L function。

好像这是唯一一个成功的抓手。大家看到这个抓手之后，就像看到了救命稻草一样，玩命往上抓，发展出各种各样的L function。但是都在同一个方向上。因为没有其他方向。

我又大放厥词了。请大能有以教我。

[TheMatrix]

来总结一下和zeta函数有关的方法 - 这些就是黎曼猜想的抓手：
1，zeta级数的定义。
2，积分定义。
3，解析延拓到全平面。
4，functional equation，zeta(s) ~ zeta(1-s)
5，Euler product

没了。我大放厥词了。请大能有以教我。

这就是为什么zeta函数特别的难。因为它没有抓手。可以说特别贫瘠。

接下来大家就开始使出浑身解数，想要硬给它安装抓手：
1，Dirichlet character modulated zeta series。Σ Χ(n)n^-s，也叫L function。

好像这是唯一一个成功的抓手。大家看到这个抓手之后，就像看到了救命稻草一样，玩命往上抓，发展出各种各样的L function。但是都在同一个方向上。因为没有其他方向。

我又大放厥词了。请大能有以教我。

zeta级数有无穷多项，它怎么能贫瘠呢？应该无穷丰富才对啊。

这是一个深刻的矛盾 - 无穷丰富和无穷贫瘠可以在一个物体上同时发生。

无穷贫瘠是作为一个整体。而无穷丰富是要进去。