#1 zeta(1/2)的几种算法
发表于 : 2023年 12月 28日 21:27
s\in (0, 1]的时候,\sum 1/n^s - 2*\sum 1/(2n)^s = \sum (-1)^(n-1) / n^s非常questionable
(ッ) 写了: 2023年 12月 29日 01:10 s\in (0, 1]的时候,\sum 1/n^s - 2*\sum 1/(2n)^s = \sum (-1)^(n-1) / n^s非常questionable
从代数方程的解,代数函数推广,想实现以奇点,零点表示函数而不是解析式或闭式表示。randomatrices 写了: 2023年 12月 29日 01:45 把我以前在版上关于解析延拓的发言再贴一下:
复变函数的精华是解析延拓。
解析延拓仿似“有物浑然天成,天然去雕琢,妙手偶得之。不增不减,此物唯一”。不似实变函数可以人工裁剪粘贴,如 y = exp(-1/x) when x > 0, y = 0, when x <= 0, 虽然在整个实数轴上无穷可微但它就不是一个天然的复平面上的解析函数, 人工斧凿总归不能胜天工。
解析延拓虽然绝大多数教课书上都是以 power series 的一个一个小收敛圆去逐渐开拓,但实际上的被研究的著名函数很少有这样被拓展的, 如黎曼 zeta 函数, 原因之一当然是因为zeta函数初定义是dirichlet series, 而dirichlet series的收敛域是部分半平面不是收敛圆。黎曼在18xx是怎么想到从复变函数去研究dirichlet series的?实在让人惊叹。
对。randomatrices 写了: 2023年 12月 29日 01:20 s\in (0, 1]的时候,当然\sum 1/n^s - 2*\sum 1/(2n)^s不等于\sum (-1)^(n-1) / n^s, 一个不收敛, 一个收敛。
但是所谓解析延拓就是, 因为在s>1时,\sum 1/n^s - 2*\sum 1/(2n)^s = \sum (-1)^(n-1) / n^s, 所以在s\in (0, 1]时,用那个收敛的级数形式\sum (-1)^(n-1) / n^s。
这就是亚纯函数的精髓啊, 在一个小的区域内定义的级数就定义了整个复平面上的函数(除掉几个奇点外), 并且是唯一的。
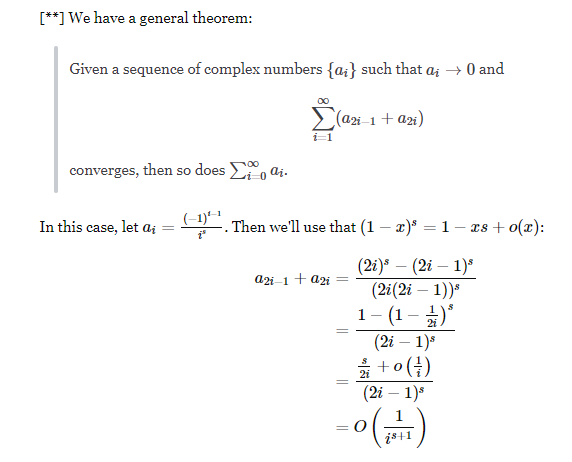
第二个也非常有意思:
解析延拓确实玄妙。randomatrices 写了: 2023年 12月 29日 01:45 把我以前在版上关于解析延拓的发言再贴一下:
复变函数的精华是解析延拓。
解析延拓仿似“有物浑然天成,天然去雕琢,妙手偶得之。不增不减,此物唯一”。不似实变函数可以人工裁剪粘贴,如 y = exp(-1/x) when x > 0, y = 0, when x <= 0, 虽然在整个实数轴上无穷可微但它就不是一个天然的复平面上的解析函数, 人工斧凿总归不能胜天工。
解析延拓虽然绝大多数教课书上都是以 power series 的一个一个小收敛圆去逐渐开拓,但实际上的被研究的著名函数很少有这样被拓展的, 如黎曼 zeta 函数, 原因之一当然是因为zeta函数初定义是dirichlet series, 而dirichlet series的收敛域是部分半平面不是收敛圆。黎曼在18xx是怎么想到从复变函数去研究dirichlet series的?实在让人惊叹。
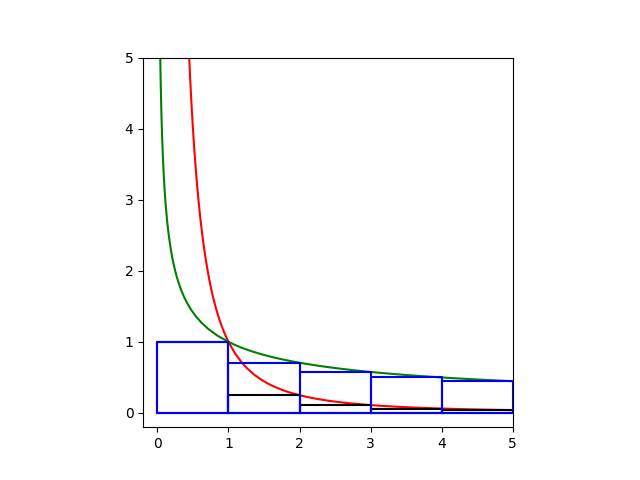
绿色的曲线是1/√x,红色的曲线是 1/x2。两条曲线是关于y=x对称的。TheMatrix 写了: 2023年 12月 29日 10:52 第二个也非常有意思:
2√N = ∫0N 1/√x,
所以ζ(1/2)比较的是
(1+1/√2+1/√3+...)
和 ∫ 1/√x。
和欧拉常数 γ 相似。所以 γ 对应 ζ(1)。
randomatrices 写了: 2023年 12月 29日 01:45 把我以前在版上关于解析延拓的发言再贴一下:
复变函数的精华是解析延拓。
解析延拓仿似“有物浑然天成,天然去雕琢,妙手偶得之。不增不减,此物唯一”。不似实变函数可以人工裁剪粘贴,如 y = exp(-1/x) when x > 0, y = 0, when x <= 0, 虽然在整个实数轴上无穷可微但它就不是一个天然的复平面上的解析函数, 人工斧凿总归不能胜天工。
解析延拓虽然绝大多数教课书上都是以 power series 的一个一个小收敛圆去逐渐开拓,但实际上的被研究的著名函数很少有这样被拓展的, 如黎曼 zeta 函数, 原因之一当然是因为zeta函数初定义是dirichlet series, 而dirichlet series的收敛域是部分半平面不是收敛圆。黎曼在18xx是怎么想到从复变函数去研究dirichlet series的?实在让人惊叹。
TheMatrix 写了: 2023年 12月 29日 11:48 解析延拓确实玄妙。
能不能说一个复变函数,只要在复平面的一个open disk上解析,就一定能够解析延拓到全平面?其中可以有一些pole。
但是能不能扩展到全复平面?
The answer is no. Power series that are lacunary enough cannot be analytically extended beyond the disk of convergence. You can google Hadamard's Gap Theorem for such results.TheMatrix 写了: 2023年 12月 29日 11:48 解析延拓确实玄妙。
能不能说一个复变函数,只要在复平面的一个open disk上解析,就一定能够解析延拓到全平面?其中可以有一些pole。
哦。谢谢。san721 写了: 2023年 12月 29日 19:03 The answer is no. Power series that are lacunary enough cannot be analytically extended beyond the disk of convergence. You can google Hadamard's Gap Theorem for such results.
natural boundaryTheMatrix 写了: 2023年 12月 29日 19:35 哦。谢谢。
查了一下,真的有这样的解析函数,只在unit disk里面解析,不能向外面扩展一点点了:Σ z2n
https://en.wikipedia.org/wiki/Lacunary_function
解了我很久的疑惑。
在unit disk边界点上,应该每一点都是essential singularity吧?
TheMatrix 写了: 2023年 12月 29日 19:35 哦。谢谢。
查了一下,真的有这样的解析函数,只在unit disk里面解析,不能向外面扩展一点点了:Σ z2n
https://en.wikipedia.org/wiki/Lacunary_function
解了我很久的疑惑。
在unit disk边界点上,应该每一点都是essential singularity吧?


