我在用permutation character/representation做。群作用在某subgroup coset上。permutation representation群矩阵简单,每行只有一个元素,而且是1。
我在找Symm(5)的6维不可约表示。我找到一个20维的permutation representation,按照character table分解,里面有一个trivial character,两个4维character(不同的),一个5维character,和一个6维的character。
我发现:
1,不管几维的表示,每个元素的eigenvalue都是root of unity,和群元素的阶有关。这个比较好理解。
2,每个矩阵都能完全对角化 - 相似对角化。也就是全部eigenvector span。这个应该也是定理吧?
所以在20维中找6维不可约表示,也就是找6维的公共不可约不变子空间,是一个组合问题。这里有对称性,但比较纷乱。
搞定了。不是用eigenvector组合的方法。而是用character的方法。这两种方法我都在想。eigenvector组合的方法也值得思考,这里有很多组合和对称。但是character的方法,如果能搞定,是更简洁的。我想出来的就是character的方法。
Symm(5),已知character table,已知有一个6维的不可约表示,已知其character。它的character,就是一个群函数,也就是这个表示空间(regular representation) 中的一个向量。全部群元素乘以这个向量,不能超出这个不可约表示的总维度。但是,regular representation中,6维的不可约表示有6个。所以全部群元素乘以这个character,会span出36维空间,等于6个6维空间的直和。所以还是要在36维空间中找6维的不变子空间。这就是困难所在。
而我用subgroup coset permutation representation,我可以任意选subgroup。得到的representation根据character table算一下,可以知道其中有哪些不可约表示。我选那种只有一个6维不可约表示的。最小的我找到一个20维的subgroup coset permutation representation。这里面有一个1维trivial表示,两个4维character(不同的),一个5维character,和一个6维的character。我就是要在这个20维空间中找到那个独一份的6维不变子空间。
这个地方我非常的满意自己。我想这个character,作为群函数,它是一个120个元素的群上的函数。我现在要找的是一个20个coset上的一个函数。如果能把120元素上的函数somehow restricted到20个coset上,是不是就直接得到我要找的6维不变子空间中的一个向量了呢?最终是成功的。但是120个元素到20个coset之间的关系,应该是什么关系?inclusion?projection?似乎没有canonical的关系。要试验。最后是projection的关系。然后每个coset里的元素的character的值相加。这是我想出的最“自然”的方法。试了一下,果不其然!
所以我就找到了20维表示中的6维不变子空间,也找到了这个不可约表示的matrix表达。
它长什么样呢?差不多都是这个样子:
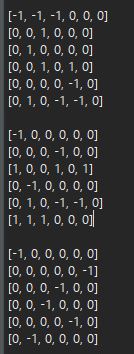
20维的表示是用subgroup coset找到的。取两个元素,生成它们的subgroup,找到subgroup的cosets。群元素也作用在cosets上,是一个permutation of cosets。这个叫permutation representation,因为相当于作用在cosets生成的线性空间上。permutation representation的character很容易计算。然后再用character table算一下其中有哪些不可约表示。我就这样循环找到两个元素,它们的coset permutation representation是20维的,包含1个1维,两个4维,1个5维,1个6维。我的目的是找到一个其中只包含1个6维的。
不是这样求。这样求肯定很慢。
是要找一个20维的向量α,这个向量在那6维的不变子空间中。然后用S5的120个元素作用在这个向量上,得到120个20维的向量。而这120个20维的向量仍然在这6维的不变子空间中 - 它们放在一起,rank=6。然后就可以在其中选出6个向量作为这个6维不变子空间的基。这样就找到这6维的不变子空间了。
所以就是要找这个α。这个α可以看成是20个点(每个点是一个coset)上的一个函数。它和character的有点像 - character是120个点(每个点是一个群元素,也可以看成是一个{e}的coset)上的一个函数。从一个character (ch)可以得到这样一个α。其赋值方法是,for a coset s, α(s)= Σ ch(g) for g in s。
这么做为什么可以呢?这个我也没证明。但是我感觉很合理 - 一试马上confirm了。呵呵。
这个我知道为什么可以了。这个叫equivariant。
我们看的是两个表示空间之间的变换:一个是regular representation空间,也就是120个群元素上的函数的空间,另一个是subgroup coset representation空间,也就是20个coset上的函数空间。这两个都是G的表示空间。我们要找的是大空间到小空间的线性变换,可以称作一个projection。
但是它必须是G-equivariant的,f(g.x)=g.f(x),也就是和G action commute。既是线性,又要G-equivariant,那只能是coset内元素值相加。G-equivariant保证了大空间中的不变子空间project到小空间后,仍然是不变子空间。
确实,group representation是研究G action,有G action的地方必须考虑G-equivariant。回头看了一下Schur Lemma和Maschke theorem,都是要求G-equivariant的,而且用G-equivariant表述也有更高一点的抽象。
Maschke theorem是construct一个G-equivariant projection,Schur Lemma是以G-equivariant为条件,研究线性变换的性质。我前面的构造也是construct一个G-equivariant projection - 从 regular representation 到 subgroup coset permutation representation。