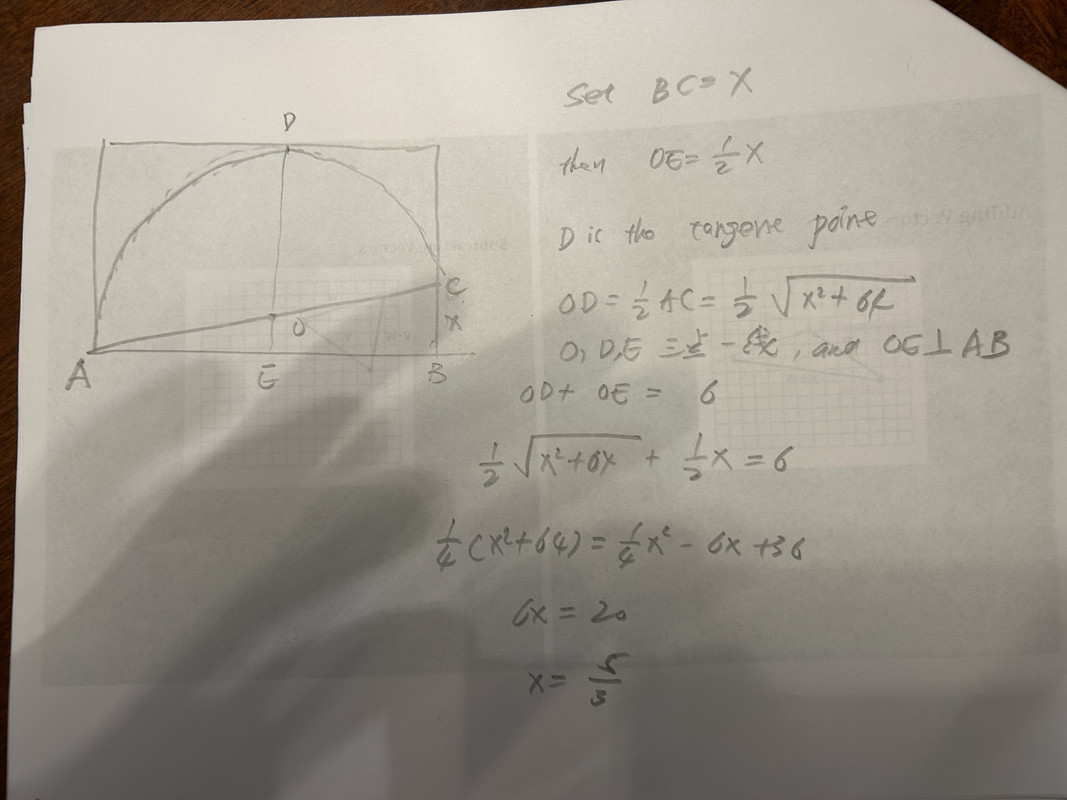
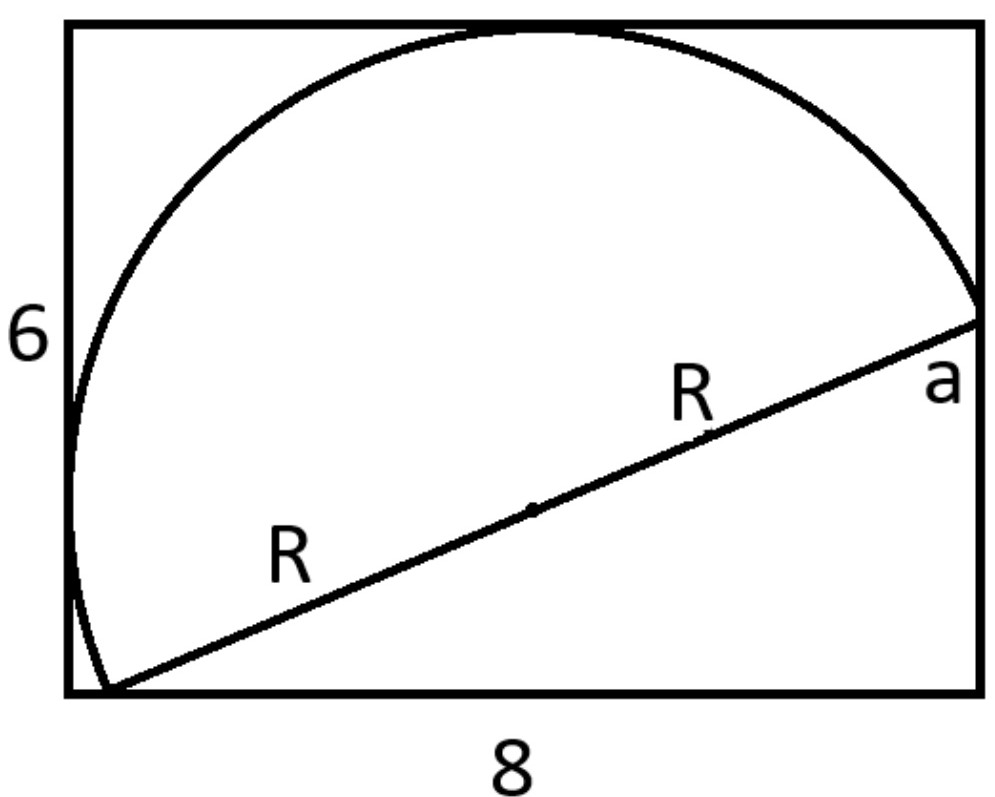
半圆左边要离开A一点点
天朝,碾压!
版主: huangchong
-
cellcycle1
- 论坛元老

cellcycle1 的博客 - 帖子互动: 883
- 帖子: 65043
- 注册时间: 2022年 7月 24日 15:59
#23 Re: 天朝,碾压!
高是 4厘米就对了, 笔误huangchong 写了: 2025年 7月 17日 13:06 因为顶上没碰着 把这个半圆一端往上偏转 可以得一个更大的半圆 另一端当然得往后缩一点 这题要仔细分析其实是比较麻烦的 但是可以假设有个半圆 一个直径靠两边 圆弧切另两边 这个形状可以想象 半径大小也不难算(高中内容)
#24 Re: 天朝,碾压!
你初中高中应该班级成绩排名不高。
rotvap 写了: 2025年 7月 17日 17:48 我觉得大家想多了
底边这样一转,必然会有一段圆弧跑到矩形外面去
必须是8的边当直径
这样两条6的边才能是切线,保证半圆不会跑出去
其实正解应该就是老师想的简单答案
#29 Re: 天朝,碾压!
R+R*cos(theta) = 8
R*sin(theta)+R = 6
solve for R and theta
To solve the system of equations:
R + R*cos(theta) = 8
R*sin(theta) + R = 6
First, factor out R from both equations:
R(1 + cos(theta)) = 8
R(1 + sin(theta)) = 6
From these, we can express R in terms of theta:
From (1): R = 8 / (1 + cos(theta))
From (2): R = 6 / (1 + sin(theta))
Since both expressions equal R, we can set them equal to each other:
8 / (1 + cos(theta)) = 6 / (1 + sin(theta))
Cross-multiply to eliminate the denominators:
8(1 + sin(theta)) = 6(1 + cos(theta))
8 + 8sin(theta) = 6 + 6cos(theta)
Rearrange the terms to get a trigonometric equation:
2 + 8sin(theta) = 6cos(theta)
Divide by 2:
1 + 4sin(theta) = 3cos(theta)
To solve this trigonometric equation, we use the tangent half-angle substitution, where t = tan(theta/2).
Recall the identities: sin(theta) = 2t / (1 + t^2) and cos(theta) = (1 - t^2) / (1 + t^2).
Substitute these into the equation:
1 + 4 * [2t / (1 + t^2)] = 3 * [(1 - t^2) / (1 + t^2)]
1 + 8t / (1 + t^2) = 3(1 - t^2) / (1 + t^2)
Multiply the entire equation by (1 + t^2) to clear the denominators:
(1 + t^2) + 8t = 3(1 - t^2)
1 + t^2 + 8t = 3 - 3t^2
Rearrange into a quadratic equation in terms of t:
t^2 + 3t^2 + 8t + 1 - 3 = 0
4t^2 + 8t - 2 = 0
Divide by 2:
2t^2 + 4t - 1 = 0
Use the quadratic formula t = [-b ± sqrt(b^2 - 4ac)] / 2a:
t = [-4 ± sqrt(4^2 - 4 * 2 * -1)] / (2 * 2)
t = [-4 ± sqrt(16 + 8)] / 4
t = [-4 ± sqrt(24)] / 4
t = [-4 ± 2*sqrt(6)] / 4
t = -1 ± sqrt(6)/2
So we have two possible values for t = tan(theta/2):
t1 = -1 + sqrt(6)/2
t2 = -1 - sqrt(6)/2
Now, we find theta from t = tan(theta/2), so theta = 2 * arctan(t).
Solution 1: Using t1 = -1 + sqrt(6)/2
theta1/2 = arctan(-1 + sqrt(6)/2)
theta1 = 2 * arctan(-1 + sqrt(6)/2)
Numerically:
sqrt(6) ≈ 2.44949
t1 ≈ -1 + 2.44949/2 ≈ -1 + 1.224745 ≈ 0.224745
theta1/2 ≈ arctan(0.224745) ≈ 0.22129 radians ≈ 12.68 degrees
theta1 ≈ 2 * 0.22129 radians ≈ 0.44258 radians ≈ 25.36 degrees
Now, find R using R = 8 / (1 + cos(theta1)) or R = 6 / (1 + sin(theta1)).
It's easier to use the exact values of cos(theta) and sin(theta) from t:
cos(theta1) = (1 - t1^2) / (1 + t1^2) and sin(theta1) = 2t1 / (1 + t1^2)
After algebraic simplification (as shown in thought process), we find:
cos(theta1) = (3 + 8sqrt(6)) / 25
sin(theta1) = (-4 + 6sqrt(6)) / 25
Substitute into R = 8 / (1 + cos(theta1)):
R1 = 8 / (1 + (3 + 8sqrt(6))/25) = 8 / ((25 + 3 + 8sqrt(6))/25) = 8 * 25 / (28 + 8sqrt(6))
R1 = 200 / (28 + 8sqrt(6)) = 50 / (7 + 2sqrt(6))
Rationalize the denominator:
R1 = 50 * (7 - 2sqrt(6)) / ((7 + 2sqrt(6))(7 - 2sqrt(6))) = 50 * (7 - 2sqrt(6)) / (49 - 4*6)
R1 = 50 * (7 - 2sqrt(6)) / (49 - 24) = 50 * (7 - 2sqrt(6)) / 25
R1 = 2 * (7 - 2sqrt(6)) = 14 - 4sqrt(6)
Numerically: R1 ≈ 14 - 4 * 2.44949 ≈ 14 - 9.79796 ≈ 4.20204
Solution 2: Using t2 = -1 - sqrt(6)/2
theta2/2 = arctan(-1 - sqrt(6)/2)
theta2 = 2 * arctan(-1 - sqrt(6)/2)
Numerically:
t2 ≈ -1 - 1.224745 ≈ -2.224745
theta2/2 ≈ arctan(-2.224745) ≈ -1.14799 radians ≈ -65.76 degrees
theta2 ≈ 2 * -1.14799 radians ≈ -2.29598 radians ≈ -131.52 degrees
To express in the range [0, 2pi), add 2pi:
theta2 ≈ -2.29598 + 2pi ≈ 3.9872 radians ≈ 228.48 degrees
Now, find R using R = 8 / (1 + cos(theta2)) or R = 6 / (1 + sin(theta2)).
cos(theta2) = (1 - t2^2) / (1 + t2^2) and sin(theta2) = 2t2 / (1 + t2^2)
After algebraic simplification, we find:
cos(theta2) = (3 - 8sqrt(6)) / 25
sin(theta2) = (-4 - 6sqrt(6)) / 25
Substitute into R = 8 / (1 + cos(theta2)):
R2 = 8 / (1 + (3 - 8sqrt(6))/25) = 8 / ((25 + 3 - 8sqrt(6))/25) = 8 * 25 / (28 - 8sqrt(6))
R2 = 200 / (28 - 8sqrt(6)) = 50 / (7 - 2sqrt(6))
Rationalize the denominator:
R2 = 50 * (7 + 2sqrt(6)) / ((7 - 2sqrt(6))(7 + 2sqrt(6))) = 50 * (7 + 2sqrt(6)) / (49 - 4*6)
R2 = 50 * (7 + 2sqrt(6)) / (49 - 24) = 50 * (7 + 2sqrt(6)) / 25
R2 = 2 * (7 + 2sqrt(6)) = 14 + 4sqrt(6)
Numerically: R2 ≈ 14 + 4 * 2.44949 ≈ 14 + 9.79796 ≈ 23.79796
Summary of Solutions:
There are two pairs of solutions for (R, theta):
Solution 1:
R = 14 - 4sqrt(6) (approximately 4.202)
theta = 2 * arctan(-1 + sqrt(6)/2) (approximately 0.4426 radians or 25.36 degrees)
Solution 2:
R = 14 + 4sqrt(6) (approximately 23.798)
theta = 2 * arctan(-1 - sqrt(6)/2) (approximately 3.9872 radians or 228.48 degrees)
Note: For the angle theta, general solutions would include adding multiples of 2π (or 360 degrees) due to the periodic nature of trigonometric functions. The provided theta values are within the range [0, 2π).).
#31 Re: 天朝,碾压!
ai?真能折腾glowinglake 写了: 2025年 7月 18日 01:12 R+R*cos(theta) = 8
R*sin(theta)+R = 6
solve for R and theta
To solve the system of equations:
R + R*cos(theta) = 8
R*sin(theta) + R = 6
First, factor out R from both equations:
R(1 + cos(theta)) = 8
R(1 + sin(theta)) = 6
From these, we can express R in terms of theta:
From (1): R = 8 / (1 + cos(theta))
From (2): R = 6 / (1 + sin(theta))
Since both expressions equal R, we can set them equal to each other:
8 / (1 + cos(theta)) = 6 / (1 + sin(theta))
Cross-multiply to eliminate the denominators:
8(1 + sin(theta)) = 6(1 + cos(theta))
8 + 8sin(theta) = 6 + 6cos(theta)
Rearrange the terms to get a trigonometric equation:
2 + 8sin(theta) = 6cos(theta)
Divide by 2:
1 + 4sin(theta) = 3cos(theta)
To solve this trigonometric equation, we use the tangent half-angle substitution, where t = tan(theta/2).
Recall the identities: sin(theta) = 2t / (1 + t^2) and cos(theta) = (1 - t^2) / (1 + t^2).
Substitute these into the equation:
1 + 4 * [2t / (1 + t^2)] = 3 * [(1 - t^2) / (1 + t^2)]
1 + 8t / (1 + t^2) = 3(1 - t^2) / (1 + t^2)
Multiply the entire equation by (1 + t^2) to clear the denominators:
(1 + t^2) + 8t = 3(1 - t^2)
1 + t^2 + 8t = 3 - 3t^2
Rearrange into a quadratic equation in terms of t:
t^2 + 3t^2 + 8t + 1 - 3 = 0
4t^2 + 8t - 2 = 0
Divide by 2:
2t^2 + 4t - 1 = 0
Use the quadratic formula t = [-b ± sqrt(b^2 - 4ac)] / 2a:
t = [-4 ± sqrt(4^2 - 4 * 2 * -1)] / (2 * 2)
t = [-4 ± sqrt(16 + 8)] / 4
t = [-4 ± sqrt(24)] / 4
t = [-4 ± 2*sqrt(6)] / 4
t = -1 ± sqrt(6)/2
So we have two possible values for t = tan(theta/2):
t1 = -1 + sqrt(6)/2
t2 = -1 - sqrt(6)/2
Now, we find theta from t = tan(theta/2), so theta = 2 * arctan(t).
Solution 1: Using t1 = -1 + sqrt(6)/2
theta1/2 = arctan(-1 + sqrt(6)/2)
theta1 = 2 * arctan(-1 + sqrt(6)/2)
Numerically:
sqrt(6) ≈ 2.44949
t1 ≈ -1 + 2.44949/2 ≈ -1 + 1.224745 ≈ 0.224745
theta1/2 ≈ arctan(0.224745) ≈ 0.22129 radians ≈ 12.68 degrees
theta1 ≈ 2 * 0.22129 radians ≈ 0.44258 radians ≈ 25.36 degrees
Now, find R using R = 8 / (1 + cos(theta1)) or R = 6 / (1 + sin(theta1)).
It's easier to use the exact values of cos(theta) and sin(theta) from t:
cos(theta1) = (1 - t1^2) / (1 + t1^2) and sin(theta1) = 2t1 / (1 + t1^2)
After algebraic simplification (as shown in thought process), we find:
cos(theta1) = (3 + 8sqrt(6)) / 25
sin(theta1) = (-4 + 6sqrt(6)) / 25
Substitute into R = 8 / (1 + cos(theta1)):
R1 = 8 / (1 + (3 + 8sqrt(6))/25) = 8 / ((25 + 3 + 8sqrt(6))/25) = 8 * 25 / (28 + 8sqrt(6))
R1 = 200 / (28 + 8sqrt(6)) = 50 / (7 + 2sqrt(6))
Rationalize the denominator:
R1 = 50 * (7 - 2sqrt(6)) / ((7 + 2sqrt(6))(7 - 2sqrt(6))) = 50 * (7 - 2sqrt(6)) / (49 - 4*6)
R1 = 50 * (7 - 2sqrt(6)) / (49 - 24) = 50 * (7 - 2sqrt(6)) / 25
R1 = 2 * (7 - 2sqrt(6)) = 14 - 4sqrt(6)
Numerically: R1 ≈ 14 - 4 * 2.44949 ≈ 14 - 9.79796 ≈ 4.20204
Solution 2: Using t2 = -1 - sqrt(6)/2
theta2/2 = arctan(-1 - sqrt(6)/2)
theta2 = 2 * arctan(-1 - sqrt(6)/2)
Numerically:
t2 ≈ -1 - 1.224745 ≈ -2.224745
theta2/2 ≈ arctan(-2.224745) ≈ -1.14799 radians ≈ -65.76 degrees
theta2 ≈ 2 * -1.14799 radians ≈ -2.29598 radians ≈ -131.52 degrees
To express in the range [0, 2pi), add 2pi:
theta2 ≈ -2.29598 + 2pi ≈ 3.9872 radians ≈ 228.48 degrees
Now, find R using R = 8 / (1 + cos(theta2)) or R = 6 / (1 + sin(theta2)).
cos(theta2) = (1 - t2^2) / (1 + t2^2) and sin(theta2) = 2t2 / (1 + t2^2)
After algebraic simplification, we find:
cos(theta2) = (3 - 8sqrt(6)) / 25
sin(theta2) = (-4 - 6sqrt(6)) / 25
Substitute into R = 8 / (1 + cos(theta2)):
R2 = 8 / (1 + (3 - 8sqrt(6))/25) = 8 / ((25 + 3 - 8sqrt(6))/25) = 8 * 25 / (28 - 8sqrt(6))
R2 = 200 / (28 - 8sqrt(6)) = 50 / (7 - 2sqrt(6))
Rationalize the denominator:
R2 = 50 * (7 + 2sqrt(6)) / ((7 - 2sqrt(6))(7 + 2sqrt(6))) = 50 * (7 + 2sqrt(6)) / (49 - 4*6)
R2 = 50 * (7 + 2sqrt(6)) / (49 - 24) = 50 * (7 + 2sqrt(6)) / 25
R2 = 2 * (7 + 2sqrt(6)) = 14 + 4sqrt(6)
Numerically: R2 ≈ 14 + 4 * 2.44949 ≈ 14 + 9.79796 ≈ 23.79796
Summary of Solutions:
There are two pairs of solutions for (R, theta):
Solution 1:
R = 14 - 4sqrt(6) (approximately 4.202)
theta = 2 * arctan(-1 + sqrt(6)/2) (approximately 0.4426 radians or 25.36 degrees)
Solution 2:
R = 14 + 4sqrt(6) (approximately 23.798)
theta = 2 * arctan(-1 - sqrt(6)/2) (approximately 3.9872 radians or 228.48 degrees)
Note: For the angle theta, general solutions would include adding multiples of 2π (or 360 degrees) due to the periodic nature of trigonometric functions. The provided theta values are within the range [0, 2π).).