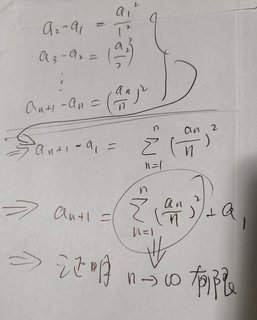阿里巴巴决赛试题
版主: Softfist
#18 Re: 阿里巴巴决赛试题
0<=a1<1
a_(n+1)= a_n + (a_n)^2/n^2
a1<1
a2= a1 + a1^2= a1(1+a1) < 2
a3= a2+ a2^2/4 = a2 (1+ a2/4) < 3
…
We can have a_n<n
a_(n+1)/a_n= 1 + a_n/n^2 < 1+ n/n^2 = 1+1/n
a_(n+1)< (1+1/n) a_n
Since Lim (1+1/n)^n = e
Then Lim(a_n) = L is bounded.
a_(n+1)= a_n + (a_n)^2/n^2
a1<1
a2= a1 + a1^2= a1(1+a1) < 2
a3= a2+ a2^2/4 = a2 (1+ a2/4) < 3
…
We can have a_n<n
a_(n+1)/a_n= 1 + a_n/n^2 < 1+ n/n^2 = 1+1/n
a_(n+1)< (1+1/n) a_n
Since Lim (1+1/n)^n = e
Then Lim(a_n) = L is bounded.
x1


#19 Re: 阿里巴巴决赛试题
17岁中专服装姜神能想到这个,非常了不起了greenspring 写了: 2024年 6月 23日 13:17 0<=a1<1
a_(n+1)= a_n + (a_n)^2/n^2
a1<1
a2= a1 + a1^2= a1(1+a1) < 2
a3= a2+ a2^2/4 = a2 (1+ a2/4) < 3
…
We can have a_n<n
a_(n+1)/a_n= 1 + a_n/n^2 < 1+ n/n^2 = 1+1/n
a_(n+1)< (1+1/n) a_n
Since Lim (1+1/n)^n = e
Then Lim(a_n) = L is bounded.
肘子急得连夜会把阿里祖坟刨了