
请问这道平几怎么做?
版主: Softfist
#2 Re: 请问这道平几怎么做?
用平面几何方法真心不会做。
但是,用解析几何方法分分钟搞定。
但是,用解析几何方法分分钟搞定。
2023年12月,张雪峰在一个直播片段中表示“文科都是服务业,什么是服务业?总结称一个字就是‘舔’,就是‘爷, 我给你笑一个’”。这一言论引发网民争议。
#4 Re: 请问这道平几怎么做?
平几能做,打好多字,麻烦死
大致上是假设角b和c不相等,不妨设角c大于角b
过b点作射线bp使得角pbo等于角c
射线bp与oe的延长线交于点p
角角边可得三角形boq和ofc全等
作线段连接p点和f点,与线段ae交于点q
pf平行于bc
然后分情况讨论,
角c是锐角时,过a点作射线ar平行于bp,射线ar与线段pf交于点r
射线bp和ca交于点s
因为ar平行于bp,角rac等于角bsc,而角bsc=角bac - 角sba,所以角rac小鱼角bac
所以r点线段qf上
过a点做垂直于ef的垂线,垂足为点t,t在线段rf上
用勾股定理知aq大于ar,而ae=eq+aq大于ar
但是角arf=角pbo=角c=角afr,所以三角形afr是等腰三角形,ar=af,得到ae大于af,矛盾
角c是直角和钝角时更简单。。
大致上是假设角b和c不相等,不妨设角c大于角b
过b点作射线bp使得角pbo等于角c
射线bp与oe的延长线交于点p
角角边可得三角形boq和ofc全等
作线段连接p点和f点,与线段ae交于点q
pf平行于bc
然后分情况讨论,
角c是锐角时,过a点作射线ar平行于bp,射线ar与线段pf交于点r
射线bp和ca交于点s
因为ar平行于bp,角rac等于角bsc,而角bsc=角bac - 角sba,所以角rac小鱼角bac
所以r点线段qf上
过a点做垂直于ef的垂线,垂足为点t,t在线段rf上
用勾股定理知aq大于ar,而ae=eq+aq大于ar
但是角arf=角pbo=角c=角afr,所以三角形afr是等腰三角形,ar=af,得到ae大于af,矛盾
角c是直角和钝角时更简单。。
#6 Re: 请问这道平几怎么做?
反证法 假设角B不等于角C
设角B大于角C 那么AC>AB 而AE=AF 则CF>BE
CF对应角2 BE对应角1 而OC=OB 那么角BEO>角CFO
那么角B + 角BEO + 角1 > 角C + 角CFO + 角2
这样两个小三角形内角和不能同为180度 矛盾
所以 角B=角C
设角B大于角C 那么AC>AB 而AE=AF 则CF>BE
CF对应角2 BE对应角1 而OC=OB 那么角BEO>角CFO
那么角B + 角BEO + 角1 > 角C + 角CFO + 角2
这样两个小三角形内角和不能同为180度 矛盾
所以 角B=角C
#9 Re: 请问这道平几怎么做?
ABC是内禀的等腰三角,反正法最迅速。
greenspring 写了: 2024年 7月 25日 08:23 反证法 假设角B不等于角C
设角B大于角C 那么AC>AB 而AE=AF 则CF>BE
CF对应角2 BE对应角1 而OC=OB 那么角BEO>角CFO
那么角B + 角BEO + 角1 > 角C + 角CFO + 角2
这样两个小三角形内角和不能同为180度 矛盾
所以 角B=角C
应运而生 在劫难逃
#10 Re: 请问这道平几怎么做?
第三步怎么得出角BEO > CFO的结论?有相关定理吗?greenspring 写了: 2024年 7月 25日 08:23 反证法 假设角B不等于角C
设角B大于角C 那么AC>AB 而AE=AF 则CF>BE
CF对应角2 BE对应角1 而OC=OB 那么角BEO>角CFO
那么角B + 角BEO + 角1 > 角C + 角CFO + 角2
这样两个小三角形内角和不能同为180度 矛盾
所以 角B=角C
#15 Re: 请问这道平几怎么做?
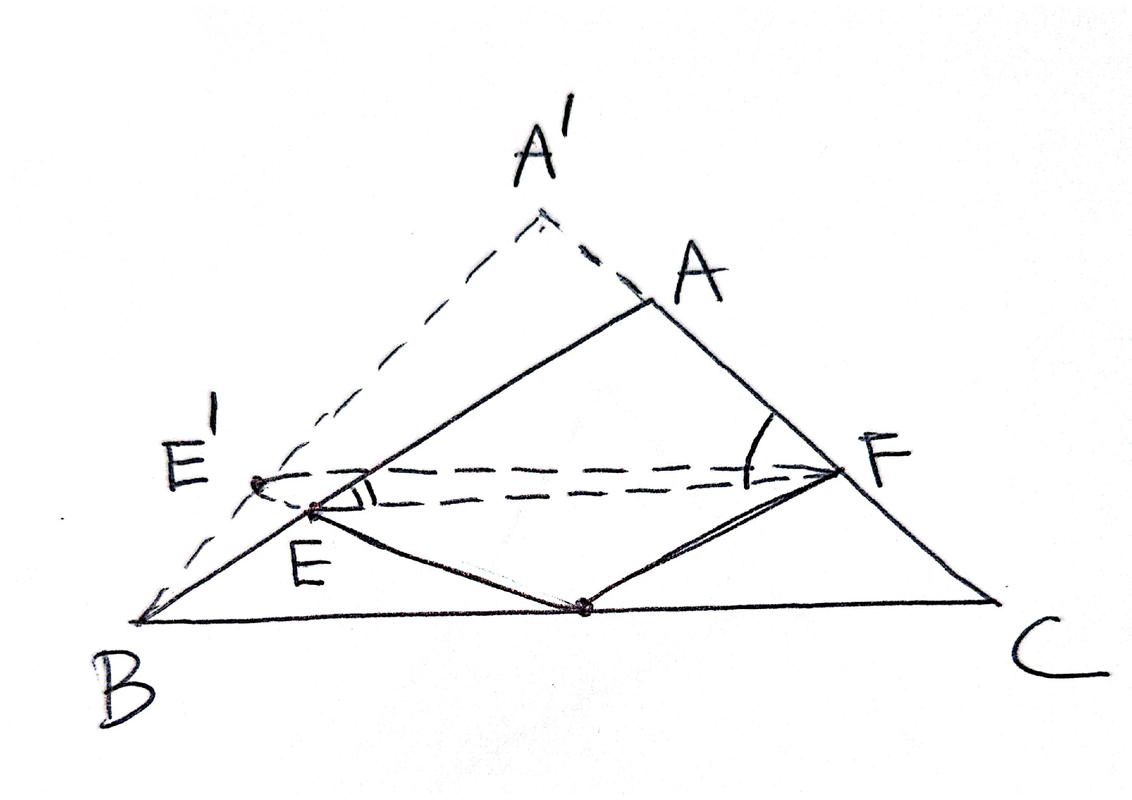
这个有点想当然,如果OE非常直立,你就不会很容易看出来了。pinwheel 写了: 2024年 7月 25日 11:51 假设角B比角C小,可以在CA延长线上找一个点A'使得BA'=CA'。然后延长OE交BA'于点E'。很容易看出来角AFE>角AFE'=角A'E'F>角AEF。
以习近平思想为指导,不忘初心,牢记使命,狠抓海外华人的思想政治工作







