DS R1 还在想，想了好几分钟了，搞了一堆积分方程，还没想明白。
各位试试看？
题目如下：
Suppose I use Rendezvous Hashing to distribute objects to different shards. At beginning I have 2 shards, once the number of objects in the shards goes over a preset threshold, I want to add a new shard. I can set this new shard's weight higher so it is more likely to get new objects. What would be a mathematically sound schema to assign weights to new shard so that the distribution of objects are still even, assuming this goes on forever?
@foxme @TheMatrix @ forecasting @ Caravel
来做题了
版主： hci
#2 Re: 来做题了
这个题目是我写码中遇到的的真实问题。
GPT 4o写答案写了一半就终止了，我让它“go on"，它才写完，你们看看对不对？
Let’s continue and refine the approach to ensure the distribution of objects remains fair and balanced while dynamically adding new shards with appropriately adjusted weights.
---
### Step 3 (Continued): Weight Assignment Strategy
We want the weight of the new shard to be slightly higher than the existing shards initially, which allows it to attract more objects when first added. However, as more shards are added, the weights of all shards should balance over time.
#### Weight Formulas:
1. **Existing Shards**:
For existing shards, scale their weights based on the current number of shards, \( n \), and ensure their total weight decreases slightly to account for the introduction of the new shard.
\[
w_i = \frac{1}{n^2}, \quad \text{for all existing shards (i = 1, 2, ..., n)}.
\]
2. **New Shard**:
The weight of the new shard is set slightly higher to initially attract more objects. A good formula for the new shard weight is:
\[
w_{new} = \frac{1}{n^2} \cdot (1 + k),
\]
where \( k \) is a small constant that determines the bias toward the new shard. For example, \( k = 1 \) means the new shard gets twice the weight of existing shards initially.
3. **Normalization**:
After assigning weights, normalize them so that the total weight \( W \) sums to 1. This ensures the probabilities are well-defined:
\[
W = \sum_{i=1}^{n} w_i + w_{new}.
\]
Normalize by dividing each weight by \( W \).
---
### Step 4: Dynamic Adjustment Over Time
As more shards are added, the weights of all shards will need to adjust dynamically to maintain fairness. The key is to reduce the bias of the new shard's weight as the total number of shards increases.
The bias factor \( k \) can be made a function of \( n \) (e.g., decrease \( k \) as \( n \) grows). For example:
\[
k = \frac{c}{n},
\]
where \( c \) is a constant. This ensures that the bias \( k \) diminishes as the number of shards increases, leading to a more uniform distribution.
---
### Algorithm for Adding a New Shard
1. **Calculate Base Weight for Existing Shards**:
Assign each existing shard a weight proportional to \( \frac{1}{n^2} \), where \( n \) is the current number of shards.
2. **Assign Weight to the New Shard**:
Use the formula:
\[
w_{new} = \frac{1}{n^2} \cdot (1 + \frac{c}{n}),
\]
where \( c \) is a constant controlling the initial bias.
3. **Normalize Weights**:
After assigning weights, normalize them so that the total weight equals 1:
\[
w_i = \frac{w_i}{W}, \quad W = \sum_{i=1}^{n+1} w_i.
\]
4. **Rehash Objects**:
Using the new weights, recompute the hash scores for each object to redistribute them among the shards.
---
### Step 5: Mathematical Soundness
This approach satisfies the following properties:
1. **Fairness**:
Over time, the weights of all shards converge to uniformity, ensuring a fair distribution of objects.
2. **Bias for New Shards**:
New shards initially attract more objects due to their slightly higher weight, which helps balance the load when they are introduced.
3. **Scalability**:
As the number of shards grows, the bias diminishes, and the system smoothly transitions to an even distribution.
---
### Example Walkthrough
#### Initial State:
Suppose you have 2 shards:
- Shard 1 weight: \( w_1 = 0.5 \),
- Shard 2 weight: \( w_2 = 0.5 \).
#### Adding a New Shard:
1. Set \( n = 2 \) (current number of shards).
2. Assign weights:
- Existing shards: \( w_1 = w_2 = \frac{1}{n^2} = \frac{1}{4} = 0.25 \),
- New shard: \( w_{new} = \frac{1}{4} \cdot (1 + \frac{1}{2}) = 0.375 \).
3. Normalize:
Total weight \( W = 0.25 + 0.25 + 0.375 = 0.875 \).
Normalized weights:
- \( w_1 = \frac{0.25}{0.875} = 0.2857 \),
- \( w_2 = \frac{0.25}{0.875} = 0.2857 \),
- \( w_{new} = \frac{0.375}{0.875} = 0.4286 \).
#### Adding Another Shard:
Repeat the process with \( n = 3 \), and so on.
---
### Conclusion
This approach ensures that new shards receive a higher weight initially, but as more shards are added, the weights converge to uniformity. The key is using a weight formula that decreases the bias dynamically as the system grows. Let me know if you have further questions!
GPT 4o写答案写了一半就终止了，我让它“go on"，它才写完，你们看看对不对？
Let’s continue and refine the approach to ensure the distribution of objects remains fair and balanced while dynamically adding new shards with appropriately adjusted weights.
---
### Step 3 (Continued): Weight Assignment Strategy
We want the weight of the new shard to be slightly higher than the existing shards initially, which allows it to attract more objects when first added. However, as more shards are added, the weights of all shards should balance over time.
#### Weight Formulas:
1. **Existing Shards**:
For existing shards, scale their weights based on the current number of shards, \( n \), and ensure their total weight decreases slightly to account for the introduction of the new shard.
\[
w_i = \frac{1}{n^2}, \quad \text{for all existing shards (i = 1, 2, ..., n)}.
\]
2. **New Shard**:
The weight of the new shard is set slightly higher to initially attract more objects. A good formula for the new shard weight is:
\[
w_{new} = \frac{1}{n^2} \cdot (1 + k),
\]
where \( k \) is a small constant that determines the bias toward the new shard. For example, \( k = 1 \) means the new shard gets twice the weight of existing shards initially.
3. **Normalization**:
After assigning weights, normalize them so that the total weight \( W \) sums to 1. This ensures the probabilities are well-defined:
\[
W = \sum_{i=1}^{n} w_i + w_{new}.
\]
Normalize by dividing each weight by \( W \).
---
### Step 4: Dynamic Adjustment Over Time
As more shards are added, the weights of all shards will need to adjust dynamically to maintain fairness. The key is to reduce the bias of the new shard's weight as the total number of shards increases.
The bias factor \( k \) can be made a function of \( n \) (e.g., decrease \( k \) as \( n \) grows). For example:
\[
k = \frac{c}{n},
\]
where \( c \) is a constant. This ensures that the bias \( k \) diminishes as the number of shards increases, leading to a more uniform distribution.
---
### Algorithm for Adding a New Shard
1. **Calculate Base Weight for Existing Shards**:
Assign each existing shard a weight proportional to \( \frac{1}{n^2} \), where \( n \) is the current number of shards.
2. **Assign Weight to the New Shard**:
Use the formula:
\[
w_{new} = \frac{1}{n^2} \cdot (1 + \frac{c}{n}),
\]
where \( c \) is a constant controlling the initial bias.
3. **Normalize Weights**:
After assigning weights, normalize them so that the total weight equals 1:
\[
w_i = \frac{w_i}{W}, \quad W = \sum_{i=1}^{n+1} w_i.
\]
4. **Rehash Objects**:
Using the new weights, recompute the hash scores for each object to redistribute them among the shards.
---
### Step 5: Mathematical Soundness
This approach satisfies the following properties:
1. **Fairness**:
Over time, the weights of all shards converge to uniformity, ensuring a fair distribution of objects.
2. **Bias for New Shards**:
New shards initially attract more objects due to their slightly higher weight, which helps balance the load when they are introduced.
3. **Scalability**:
As the number of shards grows, the bias diminishes, and the system smoothly transitions to an even distribution.
---
### Example Walkthrough
#### Initial State:
Suppose you have 2 shards:
- Shard 1 weight: \( w_1 = 0.5 \),
- Shard 2 weight: \( w_2 = 0.5 \).
#### Adding a New Shard:
1. Set \( n = 2 \) (current number of shards).
2. Assign weights:
- Existing shards: \( w_1 = w_2 = \frac{1}{n^2} = \frac{1}{4} = 0.25 \),
- New shard: \( w_{new} = \frac{1}{4} \cdot (1 + \frac{1}{2}) = 0.375 \).
3. Normalize:
Total weight \( W = 0.25 + 0.25 + 0.375 = 0.875 \).
Normalized weights:
- \( w_1 = \frac{0.25}{0.875} = 0.2857 \),
- \( w_2 = \frac{0.25}{0.875} = 0.2857 \),
- \( w_{new} = \frac{0.375}{0.875} = 0.4286 \).
#### Adding Another Shard:
Repeat the process with \( n = 3 \), and so on.
---
### Conclusion
This approach ensures that new shards receive a higher weight initially, but as more shards are added, the weights converge to uniformity. The key is using a weight formula that decreases the bias dynamically as the system grows. Let me know if you have further questions!
#3 Re: 来做题了
好了，DS R1 想好了，思维过程太长了，让我先贴一下它的解决方案吧，貌似与GTP4o的方案很不一样。你们觉得谁对谁错呢？
hci 写了： 2025年 1月 28日 00:48 DS R1 还在想，想了十几分钟了，搞了一堆积分方程，还没想明白。
各位试试看？
题目如下：
Suppose I use Rendezvous Hashing to distribute objects to different shards. At beginning I have 2 shards, once the number of shards goes over a preset threshold, I want to add a new shard. I can set this new shard's weight higher so it is more likely to get new objects. What would be a mathematically sound schema to assign weights to new shard so that the distribution of objects are still even, assuming this goes on forever?
@foxme @TheMatrix @ forecasting @ Caravel
#4 Re: 来做题了
GPT4o这个答案不符合要求。她说要“recompute the hash scores for each object to redistribute them among the shards.”，这是不可接受的。
"“recompute the hash scores for each object to redistribute them among the shards.“ is not acceptable. We want to minimize redistribution. Ideally, no redistribution."
这是新答案：
Ah, I see! Thank you for clarifying that **minimizing redistribution** (ideally **no redistribution**) is a critical requirement. This makes the problem more challenging but also aligns well with the fundamental benefit of **Rendezvous Hashing**, which is to minimize changes when shards are added or removed.
Let’s refine the solution to satisfy these constraints:
---
### Key Objective
We must:
1. **Add new shards dynamically** while ensuring that the distribution of objects remains balanced.
2. **Minimize or avoid redistribution** of objects already assigned to existing shards.
---
### Revisiting Rendezvous Hashing with Weighted Shards
In Rendezvous Hashing (also called Highest Random Weight hashing), each object is mapped to a shard by computing a weighted score for each shard. The shard with the **highest score** is chosen for the object.
For shard \( S_i \), the score for an object \( O \) is computed as:
\[
\text{score}(S_i, O) = h(S_i, O) \times w_i,
\]
where:
- \( h(S_i, O) \) is the hash of the shard \( S_i \) and object \( O \), normalized to a value between 0 and 1.
- \( w_i \) is the weight of shard \( S_i \).
Objects are assigned to the shard with the highest score. When a new shard is added, only objects that score higher for the new shard will move to it, which ensures minimal redistribution.
---
### Weight Adjustment for New Shards
We can use a **progressive weight adjustment scheme** that ensures fairness while preventing unnecessary redistribution. Here's how it works:
1. **Initial Weights for Existing Shards**:
Let the current number of shards be \( n \). Assign equal weights to all existing shards initially:
\[
w_i = 1, \quad \text{for } i = 1, 2, \dots, n.
\]
2. **Weight for the New Shard**:
When adding a new shard, assign it a higher weight (e.g., \( w_{\text{new}} > 1 \)), but scale it down progressively as more shards are added. A good choice for the new shard’s weight is:
\[
w_{\text{new}} = \frac{c}{n},
\]
where \( c > 1 \) is a constant that controls the initial bias toward the new shard. This ensures that the new shard is more likely to attract new objects, while existing objects remain largely unaffected.
3. **Dynamic Weight Normalization**:
To avoid large deviations in the distribution, normalize all weights so that the total weight remains proportional to the number of shards:
\[
\hat{w}_i = \frac{w_i}{\sum_{j=1}^{n+1} w_j}.
\]
---
### Why Redistribution Is Minimized
In Rendezvous Hashing, an object \( O \) is **only reassigned** to a new shard if the new shard’s score is higher than its current shard’s score. By carefully assigning weights to the new shard, we ensure that:
1. Most objects will remain with their original shard because the new shard’s weight is not drastically higher than the existing shards.
2. The objects that do move will naturally tend to be objects that are **better suited** for the new shard due to its higher weight.
This property of Rendezvous Hashing inherently minimizes redistribution, as only objects that are more closely associated with the new shard (based on the hash function and weights) will move.
---
### Mathematical Soundness of the Weight Scheme
The key to minimizing redistribution while maintaining fairness is to control the bias introduced by new shards. Using the weight scheme \( w_{\text{new}} = \frac{c}{n} \), we achieve the following:
1. **Initial Bias Toward New Shards**:
When the system is small (i.e., \( n \) is small), the new shard receives a relatively large weight, encouraging new objects to be assigned to it.
2. **Convergence to Uniformity**:
As \( n \) grows, \( w_{\text{new}} \) decreases, ensuring that the distribution of objects across shards becomes more uniform over time.
3. **Bounded Redistribution**:
The redistribution of objects is bounded by the difference in weights between the new shard and the existing shards. This difference decreases as \( n \) increases, leading to minimal disruption as the system grows.
---
### Example Walkthrough
#### Initial State:
Suppose there are 2 shards:
- Shard 1 weight: \( w_1 = 1 \),
- Shard 2 weight: \( w_2 = 1 \).
#### Add a New Shard:
1. Compute the new shard's weight:
\[
w_{\text{new}} = \frac{c}{n} = \frac{2}{2} = 1, \quad \text{(assuming \( c = 2 \))}.
\]
Now all shards have equal weights:
\[
w_1 = w_2 = w_{\text{new}} = 1.
\]
This results in no redistribution because the weights are balanced.
#### Add Another Shard:
1. Compute the new shard's weight:
\[
w_{\text{new}} = \frac{c}{n} = \frac{2}{3}.
\]
Normalize the weights:
\[
w_1 = w_2 = w_3 = 1, \quad w_{\text{new}} = \frac{2}{3}.
\]
Redistribution will only occur for objects that hash to a significantly higher score for the new shard, which ensures minimal disruption.
---
### Final Thoughts
By carefully controlling the weights of new shards, we can ensure that:
- Redistribution is minimized (only objects that strongly favor the new shard will move).
- The system remains balanced, with new shards initially receiving more objects but converging to uniformity over time.
This approach leverages the natural properties of Rendezvous Hashing to handle dynamic scaling gracefully without requiring a complete reassignment of objects. Let me know if you’d like further clarification or refinements!
"“recompute the hash scores for each object to redistribute them among the shards.“ is not acceptable. We want to minimize redistribution. Ideally, no redistribution."
这是新答案：
Ah, I see! Thank you for clarifying that **minimizing redistribution** (ideally **no redistribution**) is a critical requirement. This makes the problem more challenging but also aligns well with the fundamental benefit of **Rendezvous Hashing**, which is to minimize changes when shards are added or removed.
Let’s refine the solution to satisfy these constraints:
---
### Key Objective
We must:
1. **Add new shards dynamically** while ensuring that the distribution of objects remains balanced.
2. **Minimize or avoid redistribution** of objects already assigned to existing shards.
---
### Revisiting Rendezvous Hashing with Weighted Shards
In Rendezvous Hashing (also called Highest Random Weight hashing), each object is mapped to a shard by computing a weighted score for each shard. The shard with the **highest score** is chosen for the object.
For shard \( S_i \), the score for an object \( O \) is computed as:
\[
\text{score}(S_i, O) = h(S_i, O) \times w_i,
\]
where:
- \( h(S_i, O) \) is the hash of the shard \( S_i \) and object \( O \), normalized to a value between 0 and 1.
- \( w_i \) is the weight of shard \( S_i \).
Objects are assigned to the shard with the highest score. When a new shard is added, only objects that score higher for the new shard will move to it, which ensures minimal redistribution.
---
### Weight Adjustment for New Shards
We can use a **progressive weight adjustment scheme** that ensures fairness while preventing unnecessary redistribution. Here's how it works:
1. **Initial Weights for Existing Shards**:
Let the current number of shards be \( n \). Assign equal weights to all existing shards initially:
\[
w_i = 1, \quad \text{for } i = 1, 2, \dots, n.
\]
2. **Weight for the New Shard**:
When adding a new shard, assign it a higher weight (e.g., \( w_{\text{new}} > 1 \)), but scale it down progressively as more shards are added. A good choice for the new shard’s weight is:
\[
w_{\text{new}} = \frac{c}{n},
\]
where \( c > 1 \) is a constant that controls the initial bias toward the new shard. This ensures that the new shard is more likely to attract new objects, while existing objects remain largely unaffected.
3. **Dynamic Weight Normalization**:
To avoid large deviations in the distribution, normalize all weights so that the total weight remains proportional to the number of shards:
\[
\hat{w}_i = \frac{w_i}{\sum_{j=1}^{n+1} w_j}.
\]
---
### Why Redistribution Is Minimized
In Rendezvous Hashing, an object \( O \) is **only reassigned** to a new shard if the new shard’s score is higher than its current shard’s score. By carefully assigning weights to the new shard, we ensure that:
1. Most objects will remain with their original shard because the new shard’s weight is not drastically higher than the existing shards.
2. The objects that do move will naturally tend to be objects that are **better suited** for the new shard due to its higher weight.
This property of Rendezvous Hashing inherently minimizes redistribution, as only objects that are more closely associated with the new shard (based on the hash function and weights) will move.
---
### Mathematical Soundness of the Weight Scheme
The key to minimizing redistribution while maintaining fairness is to control the bias introduced by new shards. Using the weight scheme \( w_{\text{new}} = \frac{c}{n} \), we achieve the following:
1. **Initial Bias Toward New Shards**:
When the system is small (i.e., \( n \) is small), the new shard receives a relatively large weight, encouraging new objects to be assigned to it.
2. **Convergence to Uniformity**:
As \( n \) grows, \( w_{\text{new}} \) decreases, ensuring that the distribution of objects across shards becomes more uniform over time.
3. **Bounded Redistribution**:
The redistribution of objects is bounded by the difference in weights between the new shard and the existing shards. This difference decreases as \( n \) increases, leading to minimal disruption as the system grows.
---
### Example Walkthrough
#### Initial State:
Suppose there are 2 shards:
- Shard 1 weight: \( w_1 = 1 \),
- Shard 2 weight: \( w_2 = 1 \).
#### Add a New Shard:
1. Compute the new shard's weight:
\[
w_{\text{new}} = \frac{c}{n} = \frac{2}{2} = 1, \quad \text{(assuming \( c = 2 \))}.
\]
Now all shards have equal weights:
\[
w_1 = w_2 = w_{\text{new}} = 1.
\]
This results in no redistribution because the weights are balanced.
#### Add Another Shard:
1. Compute the new shard's weight:
\[
w_{\text{new}} = \frac{c}{n} = \frac{2}{3}.
\]
Normalize the weights:
\[
w_1 = w_2 = w_3 = 1, \quad w_{\text{new}} = \frac{2}{3}.
\]
Redistribution will only occur for objects that hash to a significantly higher score for the new shard, which ensures minimal disruption.
---
### Final Thoughts
By carefully controlling the weights of new shards, we can ensure that:
- Redistribution is minimized (only objects that strongly favor the new shard will move).
- The system remains balanced, with new shards initially receiving more objects but converging to uniformity over time.
This approach leverages the natural properties of Rendezvous Hashing to handle dynamic scaling gracefully without requiring a complete reassignment of objects. Let me know if you’d like further clarification or refinements!
hci 写了： 2025年 1月 28日 01:04 这个题目是我写码中遇到的的真实问题。
GPT 4o写答案写了一半就终止了，我让它“go on"，它才写完，你们看看对不对？
Let’s continue and refine the approach to ensure the distribution of objects remains fair and balanced while dynamically adding new shards with appropriately adjusted weights.
---
### Step 3 (Continued): Weight Assignment Strategy
We want the weight of the new shard to be slightly higher than the existing shards initially, which allows it to attract more objects when first added. However, as more shards are added, the weights of all shards should balance over time.
#### Weight Formulas:
1. **Existing Shards**:
For existing shards, scale their weights based on the current number of shards, \( n \), and ensure their total weight decreases slightly to account for the introduction of the new shard.
\[
w_i = \frac{1}{n^2}, \quad \text{for all existing shards (i = 1, 2, ..., n)}.
\]
2. **New Shard**:
The weight of the new shard is set slightly higher to initially attract more objects. A good formula for the new shard weight is:
\[
w_{new} = \frac{1}{n^2} \cdot (1 + k),
\]
where \( k \) is a small constant that determines the bias toward the new shard. For example, \( k = 1 \) means the new shard gets twice the weight of existing shards initially.
3. **Normalization**:
After assigning weights, normalize them so that the total weight \( W \) sums to 1. This ensures the probabilities are well-defined:
\[
W = \sum_{i=1}^{n} w_i + w_{new}.
\]
Normalize by dividing each weight by \( W \).
---
### Step 4: Dynamic Adjustment Over Time
As more shards are added, the weights of all shards will need to adjust dynamically to maintain fairness. The key is to reduce the bias of the new shard's weight as the total number of shards increases.
The bias factor \( k \) can be made a function of \( n \) (e.g., decrease \( k \) as \( n \) grows). For example:
\[
k = \frac{c}{n},
\]
where \( c \) is a constant. This ensures that the bias \( k \) diminishes as the number of shards increases, leading to a more uniform distribution.
---
### Algorithm for Adding a New Shard
1. **Calculate Base Weight for Existing Shards**:
Assign each existing shard a weight proportional to \( \frac{1}{n^2} \), where \( n \) is the current number of shards.
2. **Assign Weight to the New Shard**:
Use the formula:
\[
w_{new} = \frac{1}{n^2} \cdot (1 + \frac{c}{n}),
\]
where \( c \) is a constant controlling the initial bias.
3. **Normalize Weights**:
After assigning weights, normalize them so that the total weight equals 1:
\[
w_i = \frac{w_i}{W}, \quad W = \sum_{i=1}^{n+1} w_i.
\]
4. **Rehash Objects**:
Using the new weights, recompute the hash scores for each object to redistribute them among the shards.
---
### Step 5: Mathematical Soundness
This approach satisfies the following properties:
1. **Fairness**:
Over time, the weights of all shards converge to uniformity, ensuring a fair distribution of objects.
2. **Bias for New Shards**:
New shards initially attract more objects due to their slightly higher weight, which helps balance the load when they are introduced.
3. **Scalability**:
As the number of shards grows, the bias diminishes, and the system smoothly transitions to an even distribution.
---
### Example Walkthrough
#### Initial State:
Suppose you have 2 shards:
- Shard 1 weight: \( w_1 = 0.5 \),
- Shard 2 weight: \( w_2 = 0.5 \).
#### Adding a New Shard:
1. Set \( n = 2 \) (current number of shards).
2. Assign weights:
- Existing shards: \( w_1 = w_2 = \frac{1}{n^2} = \frac{1}{4} = 0.25 \),
- New shard: \( w_{new} = \frac{1}{4} \cdot (1 + \frac{1}{2}) = 0.375 \).
3. Normalize:
Total weight \( W = 0.25 + 0.25 + 0.375 = 0.875 \).
Normalized weights:
- \( w_1 = \frac{0.25}{0.875} = 0.2857 \),
- \( w_2 = \frac{0.25}{0.875} = 0.2857 \),
- \( w_{new} = \frac{0.375}{0.875} = 0.4286 \).
#### Adding Another Shard:
Repeat the process with \( n = 3 \), and so on.
---
### Conclusion
This approach ensures that new shards receive a higher weight initially, but as more shards are added, the weights converge to uniformity. The key is using a weight formula that decreases the bias dynamically as the system grows. Let me know if you have further questions!
#5 Re: 来做题了
这个答案应该是错的。因为早先的Shards反而得到了更多的份额。我指出这个问题，它又开始想了。
上次由 hci 在 2025年 1月 28日 01:34 修改。
原因： 未提供修改原因
原因： 未提供修改原因
#6 Re: 来做题了
还是要redistribute.不符合要求。打回去重做。
Got it! If **no redistribution of objects** is the goal when adding new shards, we need to carefully design the weight system in **Rendezvous Hashing** so that already-assigned objects remain with their current shards, and only **newly added objects** will preferentially go to the new shard(s). This is a subtle but achievable modification to standard Rendezvous Hashing.
Here’s how we can achieve this:
---
### Key Objective
1. **No redistribution** of objects already assigned to existing shards.
2. New objects should preferentially go to the newly added shard(s) to balance the load over time.
3. Ensure fairness in the long term as the system grows (i.e., eventually, all shards handle a roughly equal share of the load).
---
### Approach: Weight Adjustment Without Redistribution
In traditional **Rendezvous Hashing**, objects are distributed based on the shard with the highest weighted hash score. To avoid redistributing objects when new shards are added, we **must keep the scores of existing shards unchanged for existing objects**. This can be achieved by:
1. **Fixing the weights of existing shards** for objects already assigned.
2. Introducing the new shard(s) with a higher relative weight, but only for **new objects**.
---
### Implementation Steps
#### Step 1: Maintain Existing Assignments
For each existing shard \( S_i \), its weight \( w_i \) remains fixed for all existing objects. This ensures that the scores for these objects, computed as:
\[
\text{score}(S_i, O) = h(S_i, O) \times w_i,
\]
are unchanged, and thus the assignment of objects remains the same.
#### Step 2: Add a New Shard with Higher Weight
When a new shard \( S_{new} \) is added, assign it a relatively higher weight \( w_{new} \) compared to the existing shards. This makes the new shard more attractive for **new objects** without affecting the assignments of existing objects.
The weight \( w_{new} \) can be chosen dynamically based on the number of existing shards \( n \). For example:
\[
w_{new} = \alpha \cdot \max(w_i),
\]
where \( \alpha > 1 \) is a scaling factor (e.g., \( \alpha = 2 \)) that gives the new shard a higher weight relative to existing shards.
#### Step 3: Ensure Existing Objects Are Unchanged
Since the hash scores for existing shards and objects are unchanged, objects already assigned to a shard will remain with their current shard.
New objects will tend to go to the new shard due to its higher weight, which helps balance the load over time.
#### Step 4: Gradually Adjust Weights
If additional new shards are added, their weights can be adjusted relative to the current set of shards to ensure fairness in the long term. For example:
- Set the weight of a new shard \( S_{new} \) proportional to the inverse of the total number of shards:
\[
w_{new} = \frac{c}{n},
\]
where \( c \) is a constant controlling the initial bias.
- Normalize weights so that the overall system remains balanced.
---
### Why This Works
1. **No Redistribution**:
Existing objects are not affected because the hash scores for existing shards remain unchanged. Rendezvous Hashing ensures that an object only moves if its new shard has a higher score, which we prevent by keeping existing shard weights fixed.
2. **New Objects Prefer New Shards**:
By giving the new shard a higher weight, it will tend to win the hash scores for new objects, ensuring that it takes on more of the new load.
3. **Fairness Over Time**:
As more shards are added, their relative weights can be adjusted to ensure that the overall load distribution remains even, without impacting existing assignments.
---
### Example Walkthrough
#### Initial State:
Suppose you have two shards:
- Shard 1 (\( S_1 \)): \( w_1 = 1 \),
- Shard 2 (\( S_2 \)): \( w_2 = 1 \).
Objects are hashed and assigned based on the scores:
\[
\text{score}(S_i, O) = h(S_i, O) \times w_i.
\]
#### Add a New Shard:
1. Add a new shard \( S_3 \) with weight \( w_3 = 2 \) (higher than the existing shards).
2. For existing objects:
- Their assignments remain the same because the scores for \( S_1 \) and \( S_2 \) are unchanged.
3. For new objects:
- The new shard \( S_3 \) is more likely to win because of its higher weight \( w_3 = 2 \).
#### Add Another Shard:
1. Add another shard \( S_4 \) with weight \( w_4 = 1.5 \).
2. Repeat the process: existing objects remain with their original shards, while new objects are distributed among \( S_3 \) and \( S_4 \), with some still going to \( S_1 \) and \( S_2 \) based on their scores.
---
### Advantages of This Approach
1. **No Redistribution**:
Existing object assignments are unchanged, ensuring stability and minimizing disruption.
2. **Load Balancing**:
New objects are preferentially assigned to the new shard(s), helping balance the load dynamically.
3. **Scalability**:
As the system grows, the weights can be adjusted to ensure fairness in the long term without impacting existing assignments.
4. **Simple Implementation**:
This approach leverages the natural properties of Rendezvous Hashing, requiring only weight adjustments for new shards.
---
### Summary
To achieve **no redistribution** of existing objects while dynamically adding new shards:
1. Keep the weights of existing shards fixed for existing objects.
2. Assign a higher weight to new shards to attract new objects.
3. Gradually reduce the relative weight of new shards as the system grows to ensure fairness over time.
This approach leverages the flexibility of **Rendezvous Hashing** while maintaining stability and fairness. Let me know if you'd like further clarification!
Got it! If **no redistribution of objects** is the goal when adding new shards, we need to carefully design the weight system in **Rendezvous Hashing** so that already-assigned objects remain with their current shards, and only **newly added objects** will preferentially go to the new shard(s). This is a subtle but achievable modification to standard Rendezvous Hashing.
Here’s how we can achieve this:
---
### Key Objective
1. **No redistribution** of objects already assigned to existing shards.
2. New objects should preferentially go to the newly added shard(s) to balance the load over time.
3. Ensure fairness in the long term as the system grows (i.e., eventually, all shards handle a roughly equal share of the load).
---
### Approach: Weight Adjustment Without Redistribution
In traditional **Rendezvous Hashing**, objects are distributed based on the shard with the highest weighted hash score. To avoid redistributing objects when new shards are added, we **must keep the scores of existing shards unchanged for existing objects**. This can be achieved by:
1. **Fixing the weights of existing shards** for objects already assigned.
2. Introducing the new shard(s) with a higher relative weight, but only for **new objects**.
---
### Implementation Steps
#### Step 1: Maintain Existing Assignments
For each existing shard \( S_i \), its weight \( w_i \) remains fixed for all existing objects. This ensures that the scores for these objects, computed as:
\[
\text{score}(S_i, O) = h(S_i, O) \times w_i,
\]
are unchanged, and thus the assignment of objects remains the same.
#### Step 2: Add a New Shard with Higher Weight
When a new shard \( S_{new} \) is added, assign it a relatively higher weight \( w_{new} \) compared to the existing shards. This makes the new shard more attractive for **new objects** without affecting the assignments of existing objects.
The weight \( w_{new} \) can be chosen dynamically based on the number of existing shards \( n \). For example:
\[
w_{new} = \alpha \cdot \max(w_i),
\]
where \( \alpha > 1 \) is a scaling factor (e.g., \( \alpha = 2 \)) that gives the new shard a higher weight relative to existing shards.
#### Step 3: Ensure Existing Objects Are Unchanged
Since the hash scores for existing shards and objects are unchanged, objects already assigned to a shard will remain with their current shard.
New objects will tend to go to the new shard due to its higher weight, which helps balance the load over time.
#### Step 4: Gradually Adjust Weights
If additional new shards are added, their weights can be adjusted relative to the current set of shards to ensure fairness in the long term. For example:
- Set the weight of a new shard \( S_{new} \) proportional to the inverse of the total number of shards:
\[
w_{new} = \frac{c}{n},
\]
where \( c \) is a constant controlling the initial bias.
- Normalize weights so that the overall system remains balanced.
---
### Why This Works
1. **No Redistribution**:
Existing objects are not affected because the hash scores for existing shards remain unchanged. Rendezvous Hashing ensures that an object only moves if its new shard has a higher score, which we prevent by keeping existing shard weights fixed.
2. **New Objects Prefer New Shards**:
By giving the new shard a higher weight, it will tend to win the hash scores for new objects, ensuring that it takes on more of the new load.
3. **Fairness Over Time**:
As more shards are added, their relative weights can be adjusted to ensure that the overall load distribution remains even, without impacting existing assignments.
---
### Example Walkthrough
#### Initial State:
Suppose you have two shards:
- Shard 1 (\( S_1 \)): \( w_1 = 1 \),
- Shard 2 (\( S_2 \)): \( w_2 = 1 \).
Objects are hashed and assigned based on the scores:
\[
\text{score}(S_i, O) = h(S_i, O) \times w_i.
\]
#### Add a New Shard:
1. Add a new shard \( S_3 \) with weight \( w_3 = 2 \) (higher than the existing shards).
2. For existing objects:
- Their assignments remain the same because the scores for \( S_1 \) and \( S_2 \) are unchanged.
3. For new objects:
- The new shard \( S_3 \) is more likely to win because of its higher weight \( w_3 = 2 \).
#### Add Another Shard:
1. Add another shard \( S_4 \) with weight \( w_4 = 1.5 \).
2. Repeat the process: existing objects remain with their original shards, while new objects are distributed among \( S_3 \) and \( S_4 \), with some still going to \( S_1 \) and \( S_2 \) based on their scores.
---
### Advantages of This Approach
1. **No Redistribution**:
Existing object assignments are unchanged, ensuring stability and minimizing disruption.
2. **Load Balancing**:
New objects are preferentially assigned to the new shard(s), helping balance the load dynamically.
3. **Scalability**:
As the system grows, the weights can be adjusted to ensure fairness in the long term without impacting existing assignments.
4. **Simple Implementation**:
This approach leverages the natural properties of Rendezvous Hashing, requiring only weight adjustments for new shards.
---
### Summary
To achieve **no redistribution** of existing objects while dynamically adding new shards:
1. Keep the weights of existing shards fixed for existing objects.
2. Assign a higher weight to new shards to attract new objects.
3. Gradually reduce the relative weight of new shards as the system grows to ensure fairness over time.
This approach leverages the flexibility of **Rendezvous Hashing** while maintaining stability and fairness. Let me know if you'd like further clarification!
hci 写了： 2025年 1月 28日 01:18 GPT4o这个答案不符合要求。她说要“recompute the hash scores for each object to redistribute them among the shards.”，这是不可接受的。
"“recompute the hash scores for each object to redistribute them among the shards.“ is not acceptable. We want to minimize redistribution. Ideally, no redistribution."
这是新答案：
Ah, I see! Thank you for clarifying that **minimizing redistribution** (ideally **no redistribution**) is a critical requirement. This makes the problem more challenging but also aligns well with the fundamental benefit of **Rendezvous Hashing**, which is to minimize changes when shards are added or removed.
Let’s refine the solution to satisfy these constraints:
---
### Key Objective
We must:
1. **Add new shards dynamically** while ensuring that the distribution of objects remains balanced.
2. **Minimize or avoid redistribution** of objects already assigned to existing shards.
---
### Revisiting Rendezvous Hashing with Weighted Shards
In Rendezvous Hashing (also called Highest Random Weight hashing), each object is mapped to a shard by computing a weighted score for each shard. The shard with the **highest score** is chosen for the object.
For shard \( S_i \), the score for an object \( O \) is computed as:
\[
\text{score}(S_i, O) = h(S_i, O) \times w_i,
\]
where:
- \( h(S_i, O) \) is the hash of the shard \( S_i \) and object \( O \), normalized to a value between 0 and 1.
- \( w_i \) is the weight of shard \( S_i \).
Objects are assigned to the shard with the highest score. When a new shard is added, only objects that score higher for the new shard will move to it, which ensures minimal redistribution.
---
### Weight Adjustment for New Shards
We can use a **progressive weight adjustment scheme** that ensures fairness while preventing unnecessary redistribution. Here's how it works:
1. **Initial Weights for Existing Shards**:
Let the current number of shards be \( n \). Assign equal weights to all existing shards initially:
\[
w_i = 1, \quad \text{for } i = 1, 2, \dots, n.
\]
2. **Weight for the New Shard**:
When adding a new shard, assign it a higher weight (e.g., \( w_{\text{new}} > 1 \)), but scale it down progressively as more shards are added. A good choice for the new shard’s weight is:
\[
w_{\text{new}} = \frac{c}{n},
\]
where \( c > 1 \) is a constant that controls the initial bias toward the new shard. This ensures that the new shard is more likely to attract new objects, while existing objects remain largely unaffected.
3. **Dynamic Weight Normalization**:
To avoid large deviations in the distribution, normalize all weights so that the total weight remains proportional to the number of shards:
\[
\hat{w}_i = \frac{w_i}{\sum_{j=1}^{n+1} w_j}.
\]
---
### Why Redistribution Is Minimized
In Rendezvous Hashing, an object \( O \) is **only reassigned** to a new shard if the new shard’s score is higher than its current shard’s score. By carefully assigning weights to the new shard, we ensure that:
1. Most objects will remain with their original shard because the new shard’s weight is not drastically higher than the existing shards.
2. The objects that do move will naturally tend to be objects that are **better suited** for the new shard due to its higher weight.
This property of Rendezvous Hashing inherently minimizes redistribution, as only objects that are more closely associated with the new shard (based on the hash function and weights) will move.
---
### Mathematical Soundness of the Weight Scheme
The key to minimizing redistribution while maintaining fairness is to control the bias introduced by new shards. Using the weight scheme \( w_{\text{new}} = \frac{c}{n} \), we achieve the following:
1. **Initial Bias Toward New Shards**:
When the system is small (i.e., \( n \) is small), the new shard receives a relatively large weight, encouraging new objects to be assigned to it.
2. **Convergence to Uniformity**:
As \( n \) grows, \( w_{\text{new}} \) decreases, ensuring that the distribution of objects across shards becomes more uniform over time.
3. **Bounded Redistribution**:
The redistribution of objects is bounded by the difference in weights between the new shard and the existing shards. This difference decreases as \( n \) increases, leading to minimal disruption as the system grows.
---
### Example Walkthrough
#### Initial State:
Suppose there are 2 shards:
- Shard 1 weight: \( w_1 = 1 \),
- Shard 2 weight: \( w_2 = 1 \).
#### Add a New Shard:
1. Compute the new shard's weight:
\[
w_{\text{new}} = \frac{c}{n} = \frac{2}{2} = 1, \quad \text{(assuming \( c = 2 \))}.
\]
Now all shards have equal weights:
\[
w_1 = w_2 = w_{\text{new}} = 1.
\]
This results in no redistribution because the weights are balanced.
#### Add Another Shard:
1. Compute the new shard's weight:
\[
w_{\text{new}} = \frac{c}{n} = \frac{2}{3}.
\]
Normalize the weights:
\[
w_1 = w_2 = w_3 = 1, \quad w_{\text{new}} = \frac{2}{3}.
\]
Redistribution will only occur for objects that hash to a significantly higher score for the new shard, which ensures minimal disruption.
---
### Final Thoughts
By carefully controlling the weights of new shards, we can ensure that:
- Redistribution is minimized (only objects that strongly favor the new shard will move).
- The system remains balanced, with new shards initially receiving more objects but converging to uniformity over time.
This approach leverages the natural properties of Rendezvous Hashing to handle dynamic scaling gracefully without requiring a complete reassignment of objects. Let me know if you’d like further clarification or refinements!
上次由 hci 在 2025年 1月 28日 01:38 修改。
原因： 未提供修改原因
原因： 未提供修改原因
#7 Re: 来做题了
好了，这次想得没那么久了（第一次想了509秒，这次374秒），最后结论如下：
貌似合理。
GPT4o没有想出这个简单办法。
看来DS R1还是要更好。明天试试O1。现在要去睡觉了。
貌似合理。
GPT4o没有想出这个简单办法。
看来DS R1还是要更好。明天试试O1。现在要去睡觉了。
x1
上次由 hci 在 2025年 1月 28日 01:45 修改。
原因： 未提供修改原因
原因： 未提供修改原因
#8 Re: 来做题了
和Gemini的答案有点相似，AI回答这种问题是不是看过例题就会做，没见过的就瞎做？
1. Understanding the Challenge
Rendezvous Hashing: In this scheme, each shard has a "weight" associated with it. When assigning an object, the object's key is hashed multiple times, and the shard with the highest hash value "wins" and gets the object.
Adding Shards: As you add shards, you want to ensure:
Even Distribution: New objects should be distributed evenly across all existing shards, including the new one.
Fairness: Older shards shouldn't be starved of new objects as new shards are added.
2. Proposed Weighting Schema
To achieve even distribution and fairness, we can use a harmonic series to determine the weight of the new shard.
Initial Shards:
Start with all existing shards having equal weights. For example, if you have 2 shards, each has a weight of 1/2.
Adding a New Shard:
Calculate the weight of the new shard using the following formula:
New Shard Weight = 1 / log(N + 1)
Where N is the current number of shards.
Adjust the weights of existing shards proportionally to maintain a total weight of 1.
3. Mathematical Justification
Harmonic Series: The harmonic series (1 + 1/2 + 1/3 + 1/4 + ...) diverges, meaning it grows infinitely slowly. This ensures that:
New Shards Get Attention: The weight of new shards decreases as the number of shards increases, but it never reaches zero. This allows new shards to receive a fair share of new objects.
Existing Shards Remain Relevant: The weights of older shards decrease gradually, but they still have a significant influence on object distribution.
4. Example
Initial State (2 Shards):
Shard 1: Weight = 1/2
Shard 2: Weight = 1/2
Adding Shard 3:
New Shard Weight: 1 / log(3 + 1) ≈ 0.721
Existing Shard Weight: (1 - 0.721) / 2 ≈ 0.1395
Adding Shard 4:
New Shard Weight: 1 / log(4 + 1) ≈ 0.621
Existing Shard Weight: (1 - 0.621) / 3 ≈ 0.1263
5. Implementation Notes
Normalization: After adding a new shard, normalize the weights of all shards so that their sum equals 1.
Threshold: Determine the threshold for adding a new shard based on your system's capacity and performance requirements.
Monitoring: Monitor the distribution of objects across shards to ensure evenness and adjust the weighting schema if necessary.
This schema provides a mathematically sound approach to assigning weights to new shards in a Rendezvous Hashing system. It ensures fairness for both new and existing shards while maintaining even object distribution over time.
#9 Re: 来做题了
hci 写了： 2025年 1月 28日 00:48 DS R1 还在想，想了好几分钟了，搞了一堆积分方程，还没想明白。
各位试试看？
题目如下：
Suppose I use Rendezvous Hashing to distribute objects to different shards. At beginning I have 2 shards, once the number of shards goes over a preset threshold, I want to add a new shard. I can set this new shard's weight higher so it is more likely to get new objects. What would be a mathematically sound schema to assign weights to new shard so that the distribution of objects are still even, assuming this goes on forever?
@foxme @TheMatrix @ forecasting @ Caravel
新的是1，老的都变成0.
-
Caravel
- 论坛元老
Caravel 的博客 - 帖子互动： 561
- 帖子： 24550
- 注册时间： 2022年 7月 24日 17:21
#12 Re: 来做题了
这和流媒体， 不知道什么时候结束， 要随机取一个元素， 方法类似啊。hci 写了： 2025年 1月 28日 00:48 DS R1 还在想，想了好几分钟了，搞了一堆积分方程，还没想明白。
各位试试看？
题目如下：
Suppose I use Rendezvous Hashing to distribute objects to different shards. At beginning I have 2 shards, once the number of shards goes over a preset threshold, I want to add a new shard. I can set this new shard's weight higher so it is more likely to get new objects. What would be a mathematically sound schema to assign weights to new shard so that the distribution of objects are still even, assuming this goes on forever?
@foxme @TheMatrix @ forecasting @ Caravel
-
Caravel
- 论坛元老
Caravel 的博客 - 帖子互动： 561
- 帖子： 24550
- 注册时间： 2022年 7月 24日 17:21
#13 Re: 来做题了
4o不是reasoning model吧，长cot不行hci 写了： 2025年 1月 28日 01:41 好了，这次想得没那么久了（第一次想了509秒，这次374秒），最后结论如下：
貌似合理。
GPT4o没有想出这个简单办法。
看来DS R1还是要更好。明天试试O1。现在要去睡觉了。
#15 Re: 来做题了
O1想了一分钟（思维过程不可见），结论如下：
A convenient way to think about “evenness” in Rendezvous (HRW) Hashing is that each shard i should receive a share of objects in proportion to its relative weight Wᵢ. If you want to add shards incrementally—always giving new shards more weight at the beginning so they “catch up” on load but still converge to an even overall distribution—one mathematically clean approach is to make the weight of each shard proportional to its available capacity (or inversely proportional to its current load).
────────────────────────────────────────────────────────────────────────
Basic principle: weight ∝ (capacity − used_space)
────────────────────────────────────────────────────────────────────────
A common concrete formula is:
Wᵢ(t) = Cᵢ − Uᵢ(t)
where:
• Cᵢ is the total capacity of shard i,
• Uᵢ(t) is how much of that capacity is used at “time” t (or as you add more objects).
If all shards have the same total capacity C, then:
Wᵢ(t) = C − Uᵢ(t).
Because Rendezvous Hashing chooses the shard i that maximizes h(key, i) × Wᵢ(t) (where h is a good hash function), the probability of choosing shard i is roughly proportional to Wᵢ(t) (assuming uniform hashing). Consequently:
• A brand‑new shard j with (C − Uⱼ(t)) close to C will initially have a large weight, so it will attract new objects more aggressively.
• As soon as shard j’s used_space Uⱼ(t) increases, its weight decreases, and it no longer “over‑attracts” compared to other shards.
Hence, each shard’s “share” of new objects automatically tapers off as it fills up, leading to a long‑run even distribution of load across all shards.
────────────────────────────────────────────────────────────────────────
Key benefits of weight = (capacity − used_space)
────────────────────────────────────────────────────────────────────────
1) It works “forever.” Each time you add a shard, that shard starts with a large (C − Uᵢ) and thus quickly comes up to speed, but its weight naturally tapers off so it does not continue to over‑soak traffic after it is “caught up.”
2) There is no need for manual rebalancing or complicated feedback loops. The formula itself ensures that heavily loaded shards have (C − Uᵢ) ≈ 0 and thus get fewer new objects.
Thus, in summary, a “mathematically sound” scheme is to make each shard’s HRW weight proportional to its remaining capacity. This guarantees that, over time (and over many inserted objects), the load converges to an even distribution, no matter how many shards you add.
A convenient way to think about “evenness” in Rendezvous (HRW) Hashing is that each shard i should receive a share of objects in proportion to its relative weight Wᵢ. If you want to add shards incrementally—always giving new shards more weight at the beginning so they “catch up” on load but still converge to an even overall distribution—one mathematically clean approach is to make the weight of each shard proportional to its available capacity (or inversely proportional to its current load).
────────────────────────────────────────────────────────────────────────
Basic principle: weight ∝ (capacity − used_space)
────────────────────────────────────────────────────────────────────────
A common concrete formula is:
Wᵢ(t) = Cᵢ − Uᵢ(t)
where:
• Cᵢ is the total capacity of shard i,
• Uᵢ(t) is how much of that capacity is used at “time” t (or as you add more objects).
If all shards have the same total capacity C, then:
Wᵢ(t) = C − Uᵢ(t).
Because Rendezvous Hashing chooses the shard i that maximizes h(key, i) × Wᵢ(t) (where h is a good hash function), the probability of choosing shard i is roughly proportional to Wᵢ(t) (assuming uniform hashing). Consequently:
• A brand‑new shard j with (C − Uⱼ(t)) close to C will initially have a large weight, so it will attract new objects more aggressively.
• As soon as shard j’s used_space Uⱼ(t) increases, its weight decreases, and it no longer “over‑attracts” compared to other shards.
Hence, each shard’s “share” of new objects automatically tapers off as it fills up, leading to a long‑run even distribution of load across all shards.
────────────────────────────────────────────────────────────────────────
Key benefits of weight = (capacity − used_space)
────────────────────────────────────────────────────────────────────────
1) It works “forever.” Each time you add a shard, that shard starts with a large (C − Uᵢ) and thus quickly comes up to speed, but its weight naturally tapers off so it does not continue to over‑soak traffic after it is “caught up.”
2) There is no need for manual rebalancing or complicated feedback loops. The formula itself ensures that heavily loaded shards have (C − Uᵢ) ≈ 0 and thus get fewer new objects.
Thus, in summary, a “mathematically sound” scheme is to make each shard’s HRW weight proportional to its remaining capacity. This guarantees that, over time (and over many inserted objects), the load converges to an even distribution, no matter how many shards you add.
hci 写了： 2025年 1月 28日 01:41 好了，这次想得没那么久了（第一次想了509秒，这次374秒），最后结论如下：
貌似合理。
GPT4o没有想出这个简单办法。
看来DS R1还是要更好。明天试试O1。现在要去睡觉了。
-
TheMatrix
- 论坛支柱
2024年度优秀版主
TheMatrix 的博客 - 帖子互动： 264
- 帖子： 13241
- 注册时间： 2022年 7月 26日 00:35
#17 Re: 来做题了
我先贴一下什么是Rendezvous Hashing：hci 写了： 2025年 1月 28日 00:48 DS R1 还在想，想了好几分钟了，搞了一堆积分方程，还没想明白。
各位试试看？
题目如下：
Suppose I use Rendezvous Hashing to distribute objects to different shards. At beginning I have 2 shards, once the number of objects in the shards goes over a preset threshold, I want to add a new shard. I can set this new shard's weight higher so it is more likely to get new objects. What would be a mathematically sound schema to assign weights to new shard so that the distribution of objects are still even, assuming this goes on forever?
@foxme @TheMatrix @ forecasting @ Caravel
-
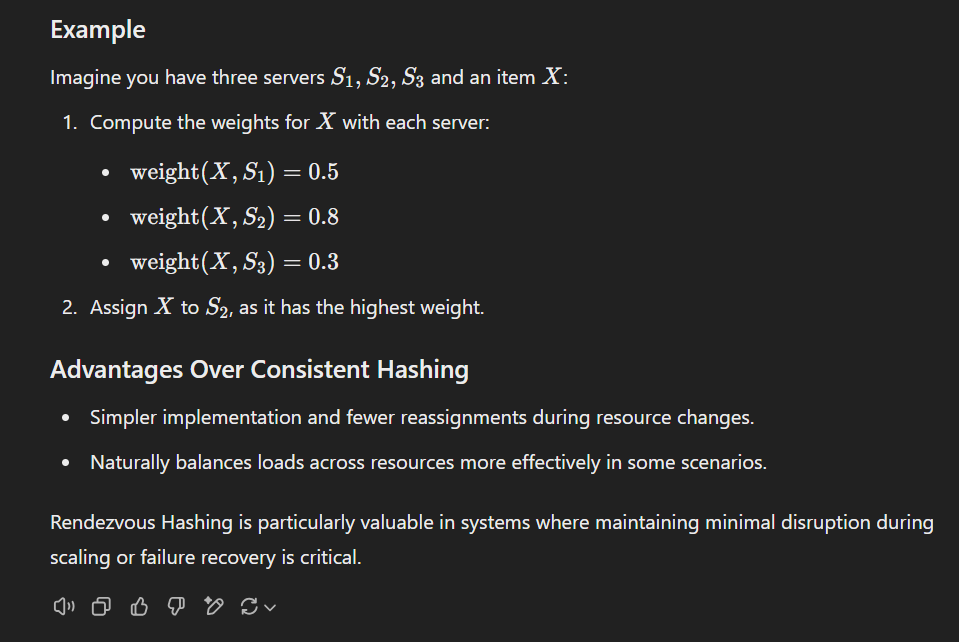
Caravel
- 论坛元老
Caravel 的博客 - 帖子互动： 561
- 帖子： 24550
- 注册时间： 2022年 7月 24日 17:21
#18 Re: 来做题了
是不是R1的cot是最厉害的？hci 写了： 2025年 1月 28日 11:59 O1的方案也有道理，但引入了一个capacity的概念，可能是看过别的地方的答案。
而R1是直接根据题目数学建模，推理过程反复进行积分计算，貌似还是更胜一筹。
#19 Re: 来做题了
它会把自己绕糊涂了。
比如第一次的错误答案，是在它把自己绕得最后得出了”这是不可能的”的结论之后，随便抛出的一个答案。当然是错的。
我指出错误之后，它才有了第二次的靠谱的答案。
就是一个实习生，有些技巧，有些知识，但缺乏智慧。
这其实也够用了。与肉人相比，就是它不会说No。明明想不出，它非要说一个错的。
比如第一次的错误答案，是在它把自己绕得最后得出了”这是不可能的”的结论之后，随便抛出的一个答案。当然是错的。
我指出错误之后，它才有了第二次的靠谱的答案。
就是一个实习生，有些技巧，有些知识，但缺乏智慧。
这其实也够用了。与肉人相比，就是它不会说No。明明想不出，它非要说一个错的。
上次由 hci 在 2025年 1月 28日 16:37 修改。
原因： 未提供修改原因
原因： 未提供修改原因
-
Caravel
- 论坛元老
Caravel 的博客 - 帖子互动： 561
- 帖子： 24550
- 注册时间： 2022年 7月 24日 17:21
#20 Re: 来做题了
有思考过程的好处是你知道他哪里想错了，可以prompt，我认为这是OAI的重大失误。hci 写了： 2025年 1月 28日 16:32 它会把自己绕糊涂了。
比如第一次的错误答案，是在它把自己绕得最后得出了”这是不可能的”的结论之后，随便抛出的一个答案。当然是错的。
我指出错误之后，它才有了第二次的靠谱的答案。