如图一
右上角水平线段为f(t)
左上角为频率图,这里看上去欧米伽为连续的任意real number
可是图二里的n为啥是整数而非任意real number?
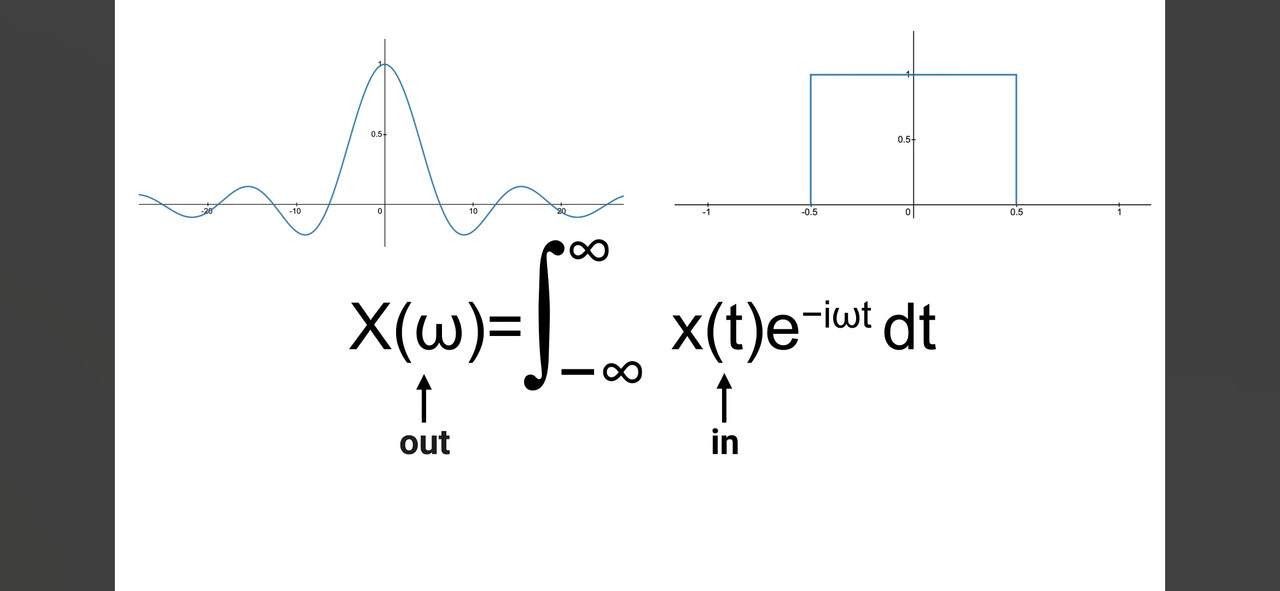
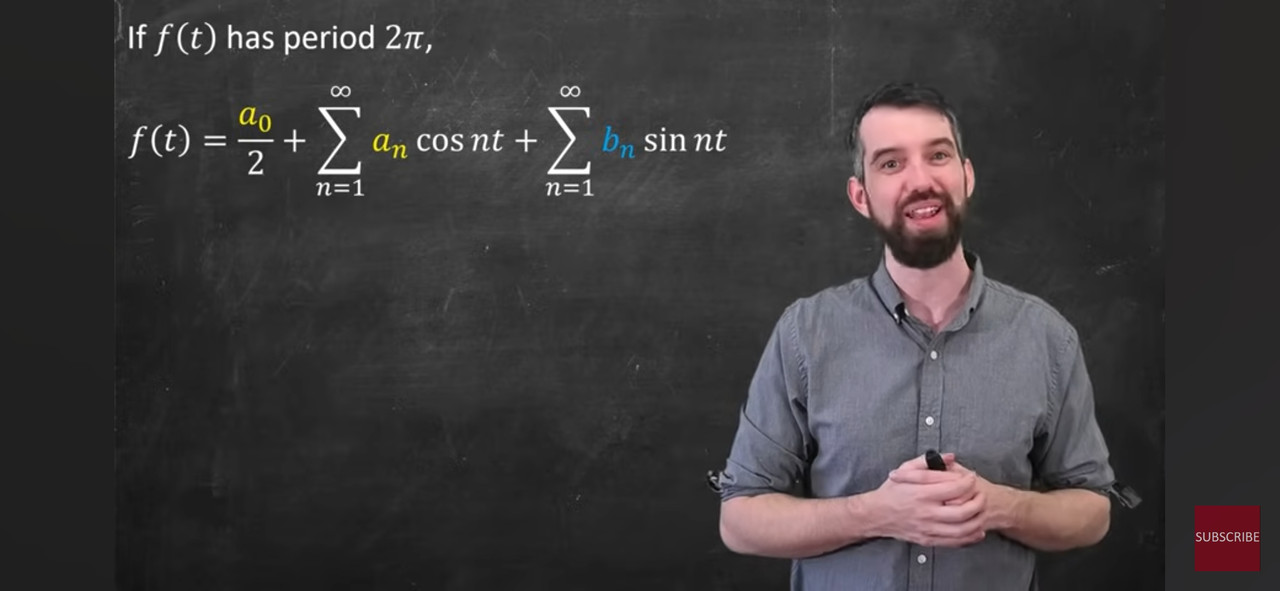
版主: Softfist

傅立叶级数是周期函数,你这里是傅立叶变换monday 写了: 2025年 3月 30日 20:53 本人初学,请高手指教
如图一
右上角水平线段为f(t)
左上角为频率图,这里看上去欧米伽为连续的任意real number
可是图二里的n为啥是整数而非任意real number?
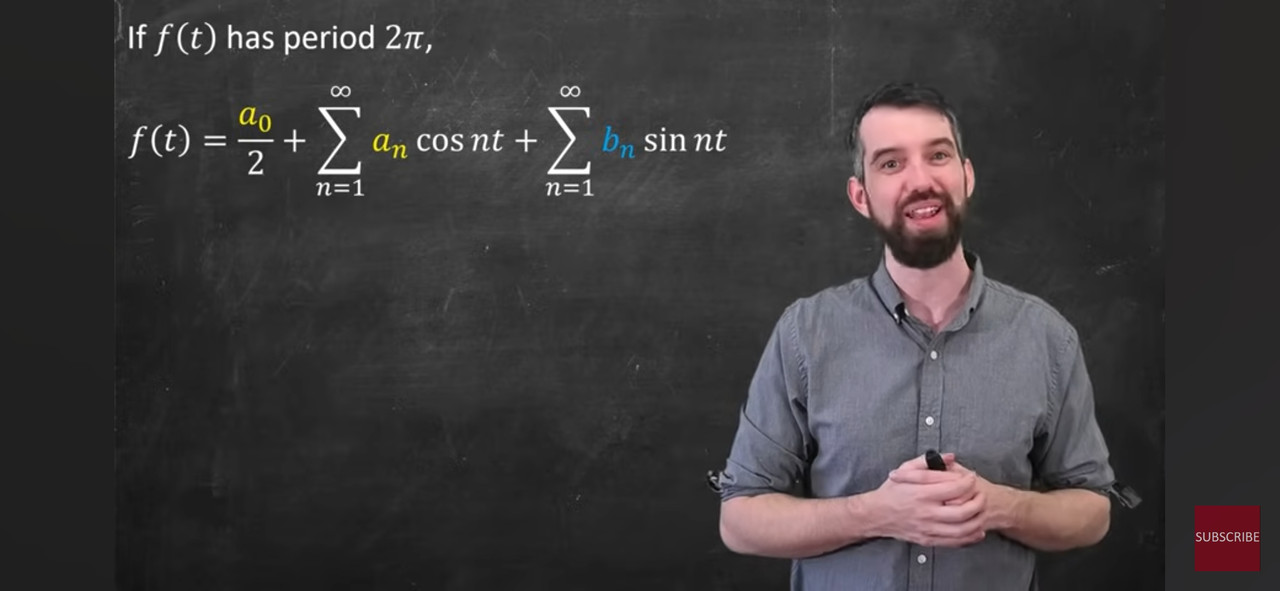
图二左上角写着:if f(t) is a function with period 2\pi。图一的f(t)显然没有这个周期。楼主需要先学图二的东西,搞明白傅里叶级数后,书上会通过padding过度到图一的傅里叶变换。monday 写了: 2025年 3月 30日 20:53 本人初学,请高手指教
如图一
右上角水平线段为f(t)
左上角为频率图,这里看上去欧米伽为连续的任意real number
可是图二里的n为啥是整数而非任意real number?
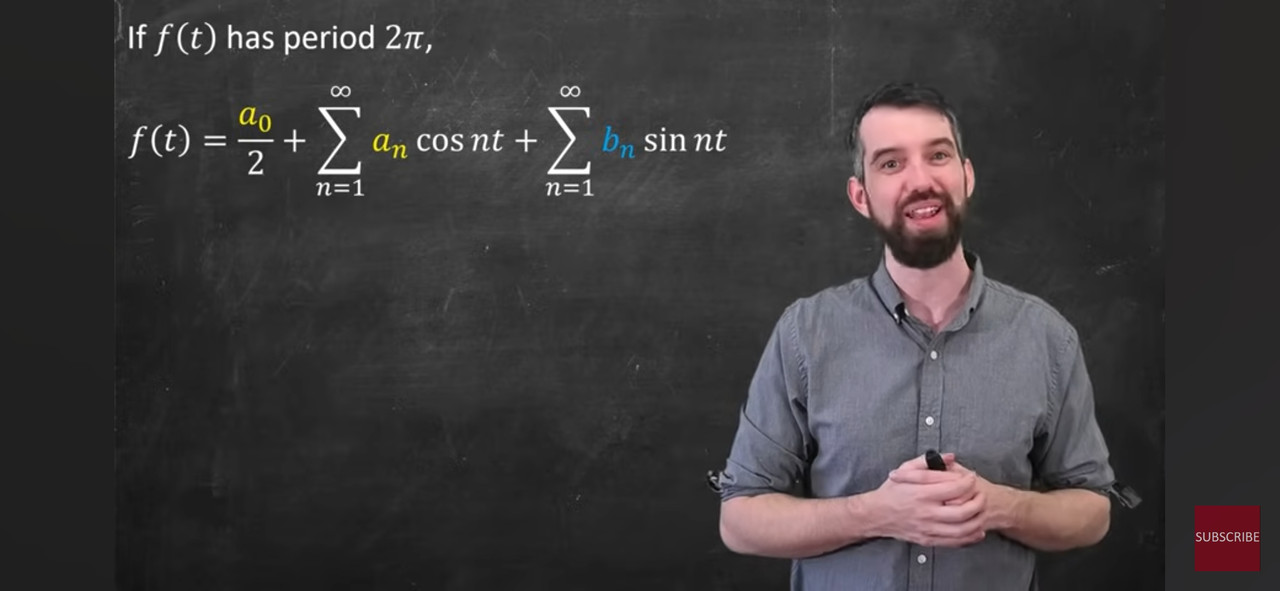
knockwood 写了: 2025年 3月 30日 21:30 变换的本质就是通过变量变换把函数形式转换,可以有很多变换方式,傅里叶变换只是一种。跟坐标系变换一个意思。如果函数没有周期,只能从连续到连续,不然自由度就缺了,变换后的函数跟之前没法表达同样的东西。如果有周期,说明函数自由度降级了,变换后函数就是整数变量函数(n序列)。不是很合理吗。
变换的本质就是在不同的基底下表示同一个函数knockwood 写了: 2025年 3月 30日 21:30 变换的本质就是通过变量变换把函数形式转换,可以有很多变换方式,傅里叶变换只是一种。跟坐标系变换一个意思。如果函数没有周期,只能从连续到连续,不然自由度就缺了,变换后的函数跟之前没法表达同样的东西。如果有周期,说明函数自由度降级了,变换后函数就是整数变量函数(n序列)。不是很合理吗。


用复数的话,两个基是一样的,都是 e^ikx, 不同的是傅立叶级数是一个固定周期T的周期函数,属于一个subsetda1gaku 写了: 2025年 4月 2日 13:53 所谓变换,就是用另一组坐标基。
傅里叶级数使用一些不同频率的正弦(余弦)函数来当坐标基,因为都是周期函数,所以相加后也只能合成周期函数。
傅里叶变换可以理解成用连续频率的正弦函数来当坐标基。因为频率连续,所以这个时候变换不能用加法,要积分。积分出来的函数可以没有周期性。
我觉得版上将军们讲得都比信号与系统这本书里清楚da1gaku 写了: 2025年 4月 2日 13:53 所谓变换,就是用另一组坐标基。
傅里叶级数使用一些不同频率的正弦(余弦)函数来当坐标基,因为都是周期函数,所以相加后也只能合成周期函数。
傅里叶变换可以理解成用连续频率的正弦函数来当坐标基。因为频率连续,所以这个时候变换不能用加法,要积分。积分出来的函数可以没有周期性。
不过“傅里叶变换”得到的是在新坐标下的“系数”(也是连续函数),如果要用它来表达原函数(也就相当于写成级数形式),要用逆变换表达式。逆变换是积分(对应级数的求和)。