群表示论中共轭类和不可约表示之间的对偶关系
版主: verdelite, TheMatrix
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
群表示论中共轭类和不可约表示之间的对偶关系
一个群的共轭类与其不可约表示的数目相等。没理由没有对应关系啊。所以我一直在想有没有canonical的对应关系。现在终于想明白了 - 没有。这两个的关系是对偶关系 - 相当于线性空间与它的对偶空间之间的关系 - 没有canonical的对应关系 - 除非指定一个关系。
可以把这个类比写更清楚:
一方面以共轭类作基生成的线性空间,叫类空间吧。比如C1,C2,C3,C4,是4个共轭类。类空间是这样的:
λ1C1+λ2C2+λ3C3+λ4C4
另一方面,共轭类上的函数,叫类函数(class function),比如 f:
f(C1) = γ1
f(C2) = γ2
f(C3) = γ3
f(C4) = γ4
类空间和类函数空间 - 是对偶的吧?这就比较清楚了。
不可约表示相当于它的character,是一个类函数,属于类函数空间。所以不和类空间比如某个共轭类直接对应。
类空间有一个自然的基,{C1,C2,C3,C4},对应类函数空间的一个对偶基:就是某个类上取1,其他类取0。指定了这种对应关系,这两个空间就可以对应上了。
但这个对偶基在群表示论中很多时候不好用。要换基 - 取不可约表示的character作基。这个基再对偶回去到类空间,,,好像又不太好使了。
可以把这个类比写更清楚:
一方面以共轭类作基生成的线性空间,叫类空间吧。比如C1,C2,C3,C4,是4个共轭类。类空间是这样的:
λ1C1+λ2C2+λ3C3+λ4C4
另一方面,共轭类上的函数,叫类函数(class function),比如 f:
f(C1) = γ1
f(C2) = γ2
f(C3) = γ3
f(C4) = γ4
类空间和类函数空间 - 是对偶的吧?这就比较清楚了。
不可约表示相当于它的character,是一个类函数,属于类函数空间。所以不和类空间比如某个共轭类直接对应。
类空间有一个自然的基,{C1,C2,C3,C4},对应类函数空间的一个对偶基:就是某个类上取1,其他类取0。指定了这种对应关系,这两个空间就可以对应上了。
但这个对偶基在群表示论中很多时候不好用。要换基 - 取不可约表示的character作基。这个基再对偶回去到类空间,,,好像又不太好使了。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 685
- 帖子: 27165
- 注册时间: 2022年 7月 24日 17:21
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
Re: 群表示论中共轭类和不可约表示之间的对偶关系
λ1C1+λ2C2+λ3C3+λ4C4
可以相当于一个类函数,f(C1)=λ1,f(C2)=λ2,f(C3)=λ3,f(C4)=λ4。(这里用了基{C1,C2,C3,C4}和其对偶基)。
f可以用不可约表示的character线性表出,但是系数不一定是整数。如果系数是整数,比如
f=n1α1+n2α2+n3α3+n4α4
那么f就是一个群表示,其中有
n1份的α1表示
n2份的α2表示
n3份的α3表示
n4份的α4表示
所以不是不可约表示,而是可约表示。
如果系数不是整数的话,这个就不能叫群表示了。这只能是一个抽象的线性组合。
Re: 群表示论中共轭类和不可约表示之间的对偶关系
这个问题我也想了一段时间,确实不存在一一对应关系(好像rgg指出过?)。但它们肯定是有关系的,这是不是就是人们说的并非canonical isomorphism?
二者相等,可以从算维数得到。看群的中心,其维数等于不可约表示的数目;看类函数空间,其维数等于共轭类的数目。
二者相等,可以从算维数得到。看群的中心,其维数等于不可约表示的数目;看类函数空间,其维数等于共轭类的数目。
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 685
- 帖子: 27165
- 注册时间: 2022年 7月 24日 17:21
Re: 群表示论中共轭类和不可约表示之间的对偶关系
f=n1α1+n2α2+n3α3+n4α4TheMatrix 写了: 2023年 1月 6日 13:05 λ1C1+λ2C2+λ3C3+λ4C4
可以相当于一个类函数,f(C1)=λ1,f(C2)=λ2,f(C3)=λ3,f(C4)=λ4。(这里用了基{C1,C2,C3,C4}和其对偶基)。
f可以用不可约表示的character线性表出,但是系数不一定是整数。如果系数是整数,比如
f=n1α1+n2α2+n3α3+n4α4
那么f就是一个群表示,其中有
n1份的α1表示
n2份的α2表示
n3份的α3表示
n4份的α4表示
所以不是不可约表示,而是可约表示。
如果系数不是整数的话,这个就不能叫群表示了。这只能是一个抽象的线性组合。
这个加号应该是direct sum把,因为作用在不同的vector space上吗
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
Re: 群表示论中共轭类和不可约表示之间的对偶关系
这个加号目前就是函数相加。这几个alpha,也就是不可约表示的character,都是类函数。可以直接加法和数乘的。
过度到vector space表示上来,我觉得还得再加一个对应:
(V1+V1...(n1 copy)) +
(V2+V2...(n2 copy)) +
+ ...
这里加号就都是direct sum了。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
Re: 群表示论中共轭类和不可约表示之间的对偶关系
对。rgg说过。FoxMe 写了: 2023年 1月 6日 13:19 这个问题我也想了一段时间,确实不存在一一对应关系(好像rgg指出过?)。但它们肯定是有关系的,这是不是就是人们说的并非canonical isomorphism?
唯一存在的一个对应是:{e}共轭类对应trivial表示。
但是和线性空间及其对偶空间的关系一样,在某些条件下对偶空间之间可以有对应关系。这个在李群中可能会更明显。因为李群的共轭类也是连续的。这是我觉得。我也不熟悉。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
Re: 群表示论中共轭类和不可约表示之间的对偶关系
比如一个线性空间V,有两组基:
A = {a1,a2,a3,a4}
B = {b1,b2,b3,b4}
这两组基之间有一个基变换X。按照指定的基顺序,X可以写成一个matrix。
一个向量v,在两组基下,各有:
v = λ1a1+λ2a2+λ3a3+λ4a4
v = γ1b1+γ2b2+γ3b3+γ4b4
v还可以看成是两组基上的函数f和g,各有:
f(a1)=λ1,f(a2)=λ2,f(a3)=λ3,f(a4)=λ4
g(b1)=γ1,g(b2)=γ2,g(b3)=γ3,g(b4)=γ4
F: f --> g 的变换就可以叫傅里叶变换。G: g --> f 的变换叫傅里叶逆变换。
进一步假设这个线性空间V还是一个代数,也就是两个向量u和v之间有乘法,u.v。那么马上可以定义另一种乘法u*v,使得 F(u*v)=F(u).F(v)。这个乘法可以叫卷积。
傅里叶变换使乘法变卷积,卷积变乘法,两个方向都是这样 - 这是从定义来的。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
Re: 群表示论中共轭类和不可约表示之间的对偶关系
看群表示也是如此。先看类函数和representation之间的关系。TheMatrix 写了: 2023年 1月 7日 12:59 比如一个线性空间V,有两组基:
A = {a1,a2,a3,a4}
B = {b1,b2,b3,b4}
这两组基之间有一个基变换X。按照指定的基顺序,X可以写成一个matrix。
一个向量v,在两组基下,各有:
v = λ1a1+λ2a2+λ3a3+λ4a4
v = γ1b1+γ2b2+γ3b3+γ4b4
v还可以看成是两组基上的函数f和g,各有:
f(a1)=λ1,f(a2)=λ2,f(a3)=λ3,f(a4)=λ4
g(b1)=γ1,g(b2)=γ2,g(b3)=γ3,g(b4)=γ4
F: f --> g 的变换就可以叫傅里叶变换。G: g --> f 的变换叫傅里叶逆变换。
进一步假设这个线性空间V还是一个代数,也就是两个向量u和v之间有乘法,u.v。那么马上可以定义另一种乘法u*v,使得 F(u*v)=F(u).F(v)。这个乘法可以叫卷积。
傅里叶变换使乘法变卷积,卷积变乘法,两个方向都是这样 - 这是从定义来的。
比如一个群G,有conjugacy class
Conj = {C1,C2,C3,C4}
Conj上的函数,就叫类函数。现在是4维。
另一方面,G有4个不可约表示:
Rep = {ρ1,ρ2,ρ3,ρ4}
还有4个对应的character:
Char = {α1,α2,α3,α4}
一个不可约character就是一个类函数,它相当于类函数空间上的另一套基。
傅里叶变换来了:
{f:Conj -> C} --> {f:Rep -> C}
{f:Rep -> C}和{f:Char -> C}是等价的。但是Char本身也是{f:Conj -> C}中的一个元素,所以有的时候会confuse。
这个傅里叶变换也有乘法到卷积,卷积到乘法。{f:Rep -> C} 那边的卷积不叫卷积,叫tensor product,但是内容是一样的。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
Re: 群表示论中共轭类和不可约表示之间的对偶关系
这是看类函数。也可以看更大的群函数空间。{f: G -> C}。而类函数空间是它的子空间 - 如果两个群元素在同一个conjugacy class里,那么它们赋同样的值。TheMatrix 写了: 2023年 1月 7日 13:26 看群表示也是如此。先看类函数和representation之间的关系。
比如一个群G,有conjugacy class
Conj = {C1,C2,C3,C4}
Conj上的函数,就叫类函数。现在是4维。
另一方面,G有4个不可约表示:
Rep = {ρ1,ρ2,ρ3,ρ4}
还有4个对应的character:
Char = {α1,α2,α3,α4}
一个不可约character就是一个类函数,它相当于类函数空间上的另一套基。
傅里叶变换来了:
{f:Conj -> C} --> {f:Rep -> C}
{f:Rep -> C}和{f:Char -> C}是等价的。但是Char本身也是{f:Conj -> C}中的一个元素,所以有的时候会confuse。
这个傅里叶变换也有乘法到卷积,卷积到乘法。{f:Rep -> C} 那边的卷积不叫卷积,叫tensor product,但是内容是一样的。
傅里叶变换怎么看成是基变换呢?这个有点难弄了。
群函数这边有“自然”的基:{δg},就是δ(g)=1,其他等于0。另一边是什么呢?另一边我们已经知道了,是matrix的直和。所以群函数这边的基就应该是这一套:
{g.α for g in G for α in Char}
g.α是g作用在α上,α是不可约表示的character,看成一个群函数。
这套数量看起来是 |G|*|Conj|,但是我们知道因为不可约表示的缘故,每一套作用都是限定在一个不变子空间中的。所以这里可以取出一套基来,而且每一套都是等价的。
傅里叶变换的另一边。是不可约方块的直和,也可以看成是matrix-valued function on Rep 或 Char。
卷积变乘法 - 这个是对的。
乘法变卷积 - 叫tensor product,应该也是对的。因为这是扩展定义,和类函数空间的定义compatible。我觉得。
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 685
- 帖子: 27165
- 注册时间: 2022年 7月 24日 17:21
Re: 群表示论中共轭类和不可约表示之间的对偶关系
dual space 和tensor也可以这么定义,定义成傅里叶变换是不是还需要一些性质?TheMatrix 写了: 2023年 1月 7日 12:59 比如一个线性空间V,有两组基:
A = {a1,a2,a3,a4}
B = {b1,b2,b3,b4}
这两组基之间有一个基变换X。按照指定的基顺序,X可以写成一个matrix。
一个向量v,在两组基下,各有:
v = λ1a1+λ2a2+λ3a3+λ4a4
v = γ1b1+γ2b2+γ3b3+γ4b4
v还可以看成是两组基上的函数f和g,各有:
f(a1)=λ1,f(a2)=λ2,f(a3)=λ3,f(a4)=λ4
g(b1)=γ1,g(b2)=γ2,g(b3)=γ3,g(b4)=γ4
F: f --> g 的变换就可以叫傅里叶变换。G: g --> f 的变换叫傅里叶逆变换。
进一步假设这个线性空间V还是一个代数,也就是两个向量u和v之间有乘法,u.v。那么马上可以定义另一种乘法u*v,使得 F(u*v)=F(u).F(v)。这个乘法可以叫卷积。
傅里叶变换使乘法变卷积,卷积变乘法,两个方向都是这样 - 这是从定义来的。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
Re: 群表示论中共轭类和不可约表示之间的对偶关系
哦。两个表示的tensor product,在character作为类函数这边变成了乘法。按照傅里叶变换把“乘法变为卷积,卷积变为乘法”的原则,tensor product这边应该可以叫卷积。不过这只是一个名字。
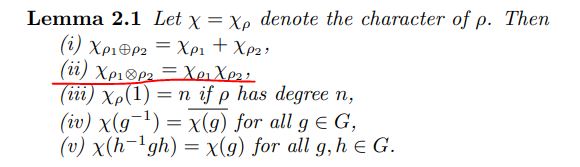
Re: 群表示论中共轭类和不可约表示之间的对偶关系
我只是从线性代数(内积空间)的角度说一句:所有不可约表示的character(记为ch_1, ch_2, ch_3, ch_4)形成类函数空间的单位正交基,每个类函数f都是ch_1, ch_2, ch_3, ch_4的线性组合,即可以写成TheMatrix 写了: 2023年 1月 6日 12:42 一个群的共轭类与其不可约表示的数目相等。没理由没有对应关系啊。所以我一直在想有没有canonical的对应关系。现在终于想明白了 - 没有。这两个的关系是对偶关系 - 相当于线性空间与它的对偶空间之间的关系 - 没有canonical的对应关系 - 除非指定一个关系。
可以把这个类比写更清楚:
一方面以共轭类作基生成的线性空间,叫类空间吧。比如C1,C2,C3,C4,是4个共轭类。类空间是这样的:
λ1C1+λ2C2+λ3C3+λ4C4
另一方面,共轭类上的函数,叫类函数(class function),比如 f:
f(C1) = γ1
f(C2) = γ2
f(C3) = γ3
f(C4) = γ4
类空间和类函数空间 - 是对偶的吧?这就比较清楚了。
不可约表示相当于它的character,是一个类函数,属于类函数空间。所以不和类空间比如某个共轭类直接对应。
类空间有一个自然的基,{C1,C2,C3,C4},对应类函数空间的一个对偶基:就是某个类上取1,其他类取0。指定了这种对应关系,这两个空间就可以对应上了。
但这个对偶基在群表示论中很多时候不好用。要换基 - 取不可约表示的character作基。这个基再对偶回去到类空间,,,好像又不太好使了。
f = λ1ch1+λ2ch2+λ3ch3+λ4ch4,
其中λi可通过f和chi的内积算出。在群表示论里,这个内积已经定义好了,想求λi算一下就出来了。
这和傅里叶变换里,cos(nx)前面的系数可通过f(x)cos(nx)的积分算出,是一个道理。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
Re: 群表示论中共轭类和不可约表示之间的对偶关系
对。内积使计算简单了。没有内积也可以算线性表出的系数,相当于解线性方程组。YWY 写了: 2023年 1月 8日 11:21 我只是从线性代数(内积空间)的角度说一句:所有不可约表示的character(记为ch_1, ch_2, ch_3, ch_4)形成类函数空间的单位正交基,每个类函数f都是ch_1, ch_2, ch_3, ch_4的线性组合,即可以写成
f = λ1ch1+λ2ch2+λ3ch3+λ4ch4,
其中λi可通过f和chi的内积算出。在群表示论里,这个内积已经定义好了,想求λi算一下就出来了。
这和傅里叶变换里,cos(nx)前面的系数可通过f(x)cos(nx)的积分算出,是一个道理。
傅里叶变换好像都有内积。
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 685
- 帖子: 27165
- 注册时间: 2022年 7月 24日 17:21
Re: 群表示论中共轭类和不可约表示之间的对偶关系
我最近看的一个材料讲了vector space的三个抽象阶梯
1.第一阶梯是集合
2.第二阶梯是数乘,加法,也就是线性性
3.第三阶梯是可以定义内积。内积还分几种,最低的是non-degenerate hermitian form,如果加上positive-definiteness,也就算(v,v) > 0 if v !=0,才是内积
我们平时碰到的一般都是到了第三阶梯。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
Re: 群表示论中共轭类和不可约表示之间的对偶关系
嗯。结构就是一层一层往上加,越来越丰富,而且加的有道理。Caravel 写了: 2023年 1月 8日 14:24 我最近看的一个材料讲了vector space的三个抽象阶梯
1.第一阶梯是集合
2.第二阶梯是数乘,加法,也就是线性性
3.第三阶梯是可以定义内积。内积还分几种,最低的是non-degenerate hermitian form,如果加上positive-definiteness,也就算(v,v) > 0 if v !=0,才是内积
我们平时碰到的一般都是到了第三阶梯。
