STEM版,合并数学,物理,化学,科学,工程,机械。不包括生物、医学相关,和计算机相关内容。
版主: verdelite , TheMatrix
FoxMe (令狐)楼主
著名点评
帖子互动: 136 帖子: 5247 注册时间: 2022年 7月 26日 16:46
帖子
由 FoxMe (令狐)楼主 2023年 3月 18日 11:08
TheMatrix 写了: 2023年 3月 17日 22:24
我的问题是,可逆元是不是都是2阶或2次的。
应该不是的,只要xx'不等于0,这里 ()' 是involution。那么逆元
x^{-1} = (xx')^{-1} x'
wugrav (老船长)
见习点评
帖子互动: 70 帖子: 1456 注册时间: 2022年 9月 18日 11:55
帖子
由 wugrav (老船长) 2023年 3月 18日 11:22
老夫用cliff代数构建标准模型的SU(3), SU(2)xU(1)群的生成元, 嚓, 多少年前的事儿了。。。。。
TheMatrix
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 264 帖子: 13215 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 2023年 3月 18日 12:50
FoxMe 写了: 2023年 3月 18日 10:59
可逆元不见得满足
y = u x u^-1,这里x, y是线性空间的向量。
由u给出的这个群就叫spin group, u就叫spinor,没看到其它的名称。我不知道可逆元是不是都是2阶或2次,感觉不大可能吧?可能要知道spin group的表示,又回到群表示论了。
嗯。我也看到了。
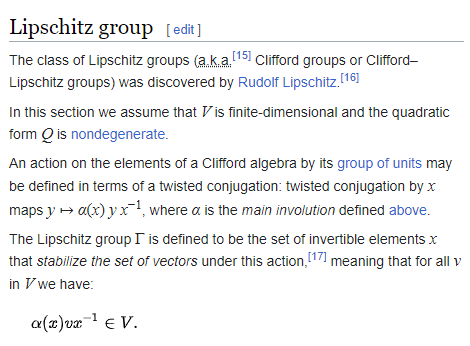
α: v -> -v 是involution。而Spin group是Lipschitz group中Q=1的偶阶元素,这里的Q是V上扩展到Clifford algebra上的。
这里的定义里有一个α,在偶阶上应该不起作用。
bigbendan
职业作家
帖子互动: 19 帖子: 588 注册时间: 2022年 10月 10日 03:02
帖子
由 bigbendan 2023年 3月 18日 12:55
hci 写了: 2023年 3月 15日 21:13
我高度怀疑这个东西是某本东方古书里的。grassmann 这个德国民科是专门研究东方古书的。
可能是用来计算我们这个虚拟现实后面的机理的。
古代道家什么都可以算,没有高深的数学,不太可能。
当你知道了虚拟现实的真相,对"物理"就失去了兴趣。都是可以算出来的东西,不必折腾了。修仙成神才是正道。
无极生太极,太极分阴阳。
灵魂通天道,虚实皆可见。
TheMatrix
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 264 帖子: 13215 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 2023年 3月 18日 12:58
FoxMe 写了: 2023年 3月 18日 11:08
应该不是的,只要xx'不等于0,这里 ()' 是involution。那么逆元
x^{-1} = (xx')^{-1} x'
嗯。Clifford algebra不是Z-grading,不能单独看2阶元素。它不是Z-grading的原因,应该是和Q以及V有关。
但是它是Z
2 -grading的,也就是分奇数阶和偶数阶的。偶数阶放在一起是一个subalgebra。
TheMatrix
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 264 帖子: 13215 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 2023年 3月 18日 16:16
FoxMe 写了: 2023年 3月 17日 18:03
长得什么样,要知道Clifford algebra的表示。很简单,就是个矩阵,没有一般的群表示论那么麻烦。我还在看。
按照群的regular representation的方法,一般algebra也可以在自身上表示,也就是algebra乘法作用的表示。Clifford algebra也有这种表示。但是表示空间比较大,是2
n 维的。
Clifford algebra有一个基础子空间V,所以就希望在V上表示。那么它的表示就应该是n-by-n矩阵。但是Clifford algebra的乘法不能保证乘以V上的一个向量之后还在V中。所以应该用共轭。因为共轭是 uvu
-1 ,互逆元素在两边作用一下,经常能保证v还在原空间中。这里已经有了u为可逆的要求。
但是共轭也不能完全保证uvu
-1 还在V中,那么就把这个要求作为一个条件,Spin group直接要求uvu
-1 仍在V中,这就满足了群表示不变子空间的要求。到这为止,相当于构造了GL(V)。再加上长度的要求,相当于从GL(V)收敛到SO(n)。
FoxMe (令狐)楼主
著名点评
帖子互动: 136 帖子: 5247 注册时间: 2022年 7月 26日 16:46
帖子
由 FoxMe (令狐)楼主 2023年 3月 18日 16:40
wugrav 写了: 2023年 3月 18日 11:22
老夫用cliff代数构建标准模型的SU(3), SU(2)xU(1)群的生成元, 嚓, 多少年前的事儿了。。。。。
介绍一下生成元的矩阵表示。
FoxMe (令狐)楼主
著名点评
帖子互动: 136 帖子: 5247 注册时间: 2022年 7月 26日 16:46
帖子
由 FoxMe (令狐)楼主 2023年 3月 18日 16:42
FoxMe 写了: 2023年 3月 18日 10:55
取名有点无厘头,很容易混淆。
单位或幺元:{x | xx=1}
单位的另一个定义:{x | 存在y,使得xy=1}
感觉很牵强。根据第二种定义,所有不等于0的实数都是单位。
我感觉单位的这个定义:{x | 存在y,使得xy=1},只有对离散的环才有意义。比如整数环的unit是 1 和 -1.
FoxMe (令狐)楼主
著名点评
帖子互动: 136 帖子: 5247 注册时间: 2022年 7月 26日 16:46
帖子
由 FoxMe (令狐)楼主 2023年 3月 18日 17:58
TheMatrix 写了: 2023年 3月 18日 12:50
α: v -> -v 是involution。而Spin group是Lipschitz group中Q=1的偶阶元素,这里的Q是V上扩展到Clifford algebra上的。
这里的定义里有一个α,在偶阶上应该不起作用。
噢,我没注意到Lipschitz group,α叫“内卷” :)
TheMatrix
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 264 帖子: 13215 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 2023年 3月 19日 11:36
这个事情使我又思考了一下纯代数扩张的问题。这是general的思考,没有具体的意义。而且有点“马太效应”,每次思考都是从差不多同样的地方开始,结束于也不比上次多多少的地方。有点像我写parser代码,我写过应该有几十个版本,每次和上次没什么太大的区别。流连忘返,我只能这么说。又像嚼口香糖,总是不肯吐掉,希望能嚼出牛肉干的味道来。
TheMatrix
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 264 帖子: 13215 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 2023年 3月 19日 13:01
TheMatrix 写了: 2023年 3月 19日 11:36
但是群本身有结构,最好要照顾到这个结构。因为我们的目的是研究群本身 - well,这是最初的目的。
虽然做代数扩张,但是还是瞄着基础空间 - 这是最初的目标。只要信息不丢失,在代数扩张上做研究,相当于给基础空间加装把手,着力点更多,研究办法更多。当然,代数扩张本身也是有意义的。
FoxMe (令狐)楼主
著名点评
帖子互动: 136 帖子: 5247 注册时间: 2022年 7月 26日 16:46
帖子
由 FoxMe (令狐)楼主 2023年 3月 19日 17:20
我总觉得tensor algebra可以用量子来实现。比如n=100时的乘法,其复杂度在2^100量级,但是用100个量子比特就行。
TheMatrix
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 264 帖子: 13215 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 2023年 3月 21日 20:00
FoxMe 写了: 2023年 3月 18日 10:59
可逆元不见得满足
y = u x u^-1,这里x, y是线性空间的向量。
由u给出的这个群就叫spin group, u就叫spinor,没看到其它的名称。我不知道可逆元是不是都是2阶或2次,感觉不大可能吧?可能要知道spin group的表示,又回到群表示论了。
Clifford algebra 里面可逆元素的比例有多大?我感觉我的想象似乎不对:我以为只有很少量的可逆元素。但是看了Cl
0,1 , Cl
0,2 , Cl
0,3 ,除了0之外都是可逆的,好像都是division ring。更高维不知道是不是也这样?
FoxMe (令狐)楼主
著名点评
帖子互动: 136 帖子: 5247 注册时间: 2022年 7月 26日 16:46
帖子
由 FoxMe (令狐)楼主 2023年 3月 22日 17:23
一般应该不是的。Cl0,1, Cl0,2刚好是复数和quaternion,Cl0,3不是。
TheMatrix
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 264 帖子: 13215 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 2023年 3月 22日 20:19
FoxMe 写了: 2023年 3月 22日 17:23
一般应该不是的。Cl0,1, Cl0,2刚好是复数和quaternion,Cl0,3不是。
不知道不可逆的元素按照basis写出来什么样,形如e
1 e
2 + e
3 e
4 这样的。
可逆但不stabilize V的元素什么样,就是uxu
-1 不在V内的那种u。
TheMatrix
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 264 帖子: 13215 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 2023年 3月 23日 16:16
Clifford algebra上也可以定义二次型Q,是从基底空间V上的二次型Q扩展上去的。这个扩展是不是canonical的,值得考虑。1 e3 e4 这样的,而不是e1 e2 +e3 e4 这样的,都可以反向相乘,变成e4 e3 e1 。这叫转置,transpose。注意对于纯乘法项x,xt x是一个数。相加的那种也可以转置,就是每一项分别转置再相加。t x的常数项。这个应该也等于每一个纯乘法项的Q再相加。
rgg
知名作家
帖子互动: 87 帖子: 1116 注册时间: 2022年 9月 12日 15:00
帖子
由 rgg 2023年 3月 23日 16:47
TheMatrix 写了: 2023年 3月 23日 16:16
Clifford algebra上也可以定义二次型Q,是从基底空间V上的二次型Q扩展上去的。这个扩展是不是canonical的,值得考虑。
首先每一个纯乘法项,比如e
1 e
3 e
4 这样的,而不是e
1 e
2 +e
3 e
4 这样的,都可以反向相乘,变成e
4 e
3 e
1 。这叫转置,transpose。注意对于纯乘法项x,x
t x是一个数。相加的那种也可以转置,就是每一项分别转置再相加。
然后,Clifford algebra上任意元素x的Q,定义为Q(x)= x
t x的常数项。这个应该也等于每一个纯乘法项的Q再相加。
内乘也可以从V上扩展到Clifford algebra上。
参见
Geometric_algebra#Extensions_of_the_inner_and_exterior_products 上面是的第三种内积定义*.
FoxMe (令狐)楼主
著名点评
帖子互动: 136 帖子: 5247 注册时间: 2022年 7月 26日 16:46
帖子
由 FoxMe (令狐)楼主 2023年 3月 23日 17:42
不错,Q(xy)=Q(x)Q(y),满足norm的乘性。
TheMatrix
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 264 帖子: 13215 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 2023年 3月 23日 18:30
嗯,看来内积的扩展确实不止一种,而且不能说哪种是canonical的。
TheMatrix
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 264 帖子: 13215 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 2023年 3月 23日 18:31
FoxMe 写了: 2023年 3月 23日 17:42
不错,Q(xy)=Q(x)Q(y),满足norm的乘性。
norm应该有乘性吗?