Clifford algebra继续讨论

[FoxMe]

我的问题是，可逆元是不是都是2阶或2次的。

应该不是的，只要xx'不等于0,这里 ()' 是involution。那么逆元
x^{-1} = (xx')^{-1} x'

[wugrav]

老夫用cliff代数构建标准模型的SU(3), SU(2)xU(1）群的生成元， 嚓， 多少年前的事儿了。。。。。

[TheMatrix]

可逆元不见得满足

y = u x u^-1，这里x, y是线性空间的向量。

由u给出的这个群就叫spin group, u就叫spinor，没看到其它的名称。我不知道可逆元是不是都是2阶或2次，感觉不大可能吧？可能要知道spin group的表示，又回到群表示论了。

嗯。我也看到了。



α: v -> -v 是involution。而Spin group是Lipschitz group中Q=1的偶阶元素，这里的Q是V上扩展到Clifford algebra上的。

这里的定义里有一个α，在偶阶上应该不起作用。

[bigbendan]

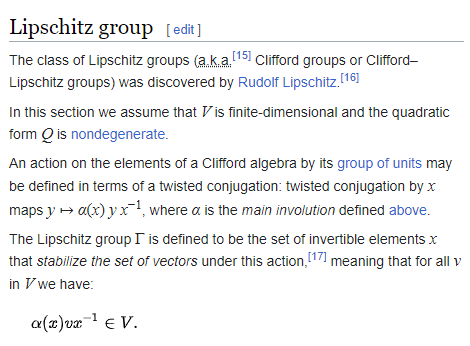
我高度怀疑这个东西是某本东方古书里的。grassmann 这个德国民科是专门研究东方古书的。

可能是用来计算我们这个虚拟现实后面的机理的。

古代道家什么都可以算，没有高深的数学，不太可能。

当你知道了虚拟现实的真相，对＂物理＂就失去了兴趣。都是可以算出来的东西，不必折腾了。修仙成神才是正道。

无极生太极，太极分阴阳。
灵魂通天道，虚实皆可见。

[TheMatrix]

应该不是的，只要xx'不等于0,这里 ()' 是involution。那么逆元
x^{-1} = (xx')^{-1} x'

嗯。Clifford algebra不是Z-grading，不能单独看2阶元素。它不是Z-grading的原因，应该是和Q以及V有关。

但是它是Z₂-grading的，也就是分奇数阶和偶数阶的。偶数阶放在一起是一个subalgebra。

[TheMatrix]

长得什么样，要知道Clifford algebra的表示。很简单，就是个矩阵，没有一般的群表示论那么麻烦。我还在看。

按照群的regular representation的方法，一般algebra也可以在自身上表示，也就是algebra乘法作用的表示。Clifford algebra也有这种表示。但是表示空间比较大，是2ⁿ维的。

Clifford algebra有一个基础子空间V，所以就希望在V上表示。那么它的表示就应该是n-by-n矩阵。但是Clifford algebra的乘法不能保证乘以V上的一个向量之后还在V中。所以应该用共轭。因为共轭是 uvu^-1，互逆元素在两边作用一下，经常能保证v还在原空间中。这里已经有了u为可逆的要求。

但是共轭也不能完全保证uvu^-1还在V中，那么就把这个要求作为一个条件，Spin group直接要求uvu^-1仍在V中，这就满足了群表示不变子空间的要求。到这为止，相当于构造了GL(V)。再加上长度的要求，相当于从GL(V)收敛到SO(n)。

[FoxMe]

老夫用cliff代数构建标准模型的SU(3), SU(2)xU(1）群的生成元， 嚓， 多少年前的事儿了。。。。。

介绍一下生成元的矩阵表示。

[FoxMe]

取名有点无厘头，很容易混淆。

单位或幺元：{x | xx=1}
单位的另一个定义：{x | 存在y，使得xy=1}

感觉很牵强。根据第二种定义，所有不等于0的实数都是单位。

我感觉单位的这个定义：{x | 存在y，使得xy=1}，只有对离散的环才有意义。比如整数环的unit是 1 和 -1.

[FoxMe]

α: v -> -v 是involution。而Spin group是Lipschitz group中Q=1的偶阶元素，这里的Q是V上扩展到Clifford algebra上的。

这里的定义里有一个α，在偶阶上应该不起作用。

噢，我没注意到Lipschitz group，α叫“内卷” ：）

[TheMatrix]

这个事情使我又思考了一下纯代数扩张的问题。这是general的思考，没有具体的意义。而且有点“马太效应”，每次思考都是从差不多同样的地方开始，结束于也不比上次多多少的地方。有点像我写parser代码，我写过应该有几十个版本，每次和上次没什么太大的区别。流连忘返，我只能这么说。又像嚼口香糖，总是不肯吐掉，希望能嚼出牛肉干的味道来。

任何东西都可以线性化或者代数化，比如一个集合S，没有任何结构，要把它线性化，就是让它point到一个target space，一个域，F，也就是考虑 {f: S -> F} 这个函数空间。立刻就线性化了。这也可以叫vector space spanned by S，或者就F-linear combination of S。而且S嵌入其中，canonically - 研究S完全包含在研究这个线性化的空间之中。

不仅线性化了，还代数化了，因为F上的乘法自然扩展到 {f: S -> F} 这个函数空间。

群也可以线性化和代数化，用同样的方法。考虑 {f: G -> F} 这个函数空间，或者F-linear combination of G。这已经是一个线性空间也是一个代数了。但是群本身有结构，最好要照顾到这个结构。因为我们的目的是研究群本身 - well，这是最初的目的。那就是 F[G]，group algebra，乘法的时候不仅target space相乘，source space也相乘。研究G完全包含在研究F[G]之中。

向量空间或线性空间本身怎么代数化？{f: V -> F}？这是一个（线性）泛函空间。上面的方法可以做，但是意义不大，因为扩张之后没有照顾到V本身的线性结构。最小的扩张是张量代数。well，我觉得应该有不同方向的扩张，张量代数是一个方向。对称代数和外代数是有限定的张量代数。

Clifford algebra，需要额外的信息，二次型Q，或者内积。内积有很多，构成一个空间。所以Clifford algebra可以说是把特定的内积结构编码到V的扩张之中了。

接下来看乘法。乘法是在加法之上的结构，有分配律。对乘法和加法的看法不同，乘法可以看成是作用，action，外部的，happen to be acting on itself。所以可以有很多不同的乘法。既然是action，那就可以研究表示，representation。线性空间已经有了，就是自己，后者自己的线性化。action就用自己的乘法。这就是regular representation。

还有一个是conjugate action，conjugate representation，值得研究。

[TheMatrix]

但是群本身有结构，最好要照顾到这个结构。因为我们的目的是研究群本身 - well，这是最初的目的。

虽然做代数扩张，但是还是瞄着基础空间 - 这是最初的目标。只要信息不丢失，在代数扩张上做研究，相当于给基础空间加装把手，着力点更多，研究办法更多。当然，代数扩张本身也是有意义的。

[FoxMe]

我总觉得tensor algebra可以用量子来实现。比如n=100时的乘法，其复杂度在2^100量级，但是用100个量子比特就行。

[TheMatrix]

可逆元不见得满足

y = u x u^-1，这里x, y是线性空间的向量。

由u给出的这个群就叫spin group, u就叫spinor，没看到其它的名称。我不知道可逆元是不是都是2阶或2次，感觉不大可能吧？可能要知道spin group的表示，又回到群表示论了。

Clifford algebra 里面可逆元素的比例有多大？我感觉我的想象似乎不对：我以为只有很少量的可逆元素。但是看了Cl_0,1, Cl_0,2, Cl_0,3，除了0之外都是可逆的，好像都是division ring。更高维不知道是不是也这样？

[FoxMe]

一般应该不是的。Cl0,1, Cl0,2刚好是复数和quaternion，Cl0,3不是。

[TheMatrix]

一般应该不是的。Cl0,1, Cl0,2刚好是复数和quaternion，Cl0,3不是。

不知道不可逆的元素按照basis写出来什么样，形如e₁e₂+ e₃e₄这样的。

可逆但不stabilize V的元素什么样，就是uxu^-1不在V内的那种u。

[TheMatrix]

Clifford algebra上也可以定义二次型Q，是从基底空间V上的二次型Q扩展上去的。这个扩展是不是canonical的，值得考虑。

首先每一个纯乘法项，比如e₁e₃e₄这样的，而不是e₁e₂+e₃e₄这样的，都可以反向相乘，变成e₄e₃e₁。这叫转置，transpose。注意对于纯乘法项x，x^tx是一个数。相加的那种也可以转置，就是每一项分别转置再相加。

然后，Clifford algebra上任意元素x的Q，定义为Q(x)= x^tx的常数项。这个应该也等于每一个纯乘法项的Q再相加。

内乘也可以从V上扩展到Clifford algebra上。

[rgg]

Clifford algebra上也可以定义二次型Q，是从基底空间V上的二次型Q扩展上去的。这个扩展是不是canonical的，值得考虑。

首先每一个纯乘法项，比如e₁e₃e₄这样的，而不是e₁e₂+e₃e₄这样的，都可以反向相乘，变成e₄e₃e₁。这叫转置，transpose。注意对于纯乘法项x，x^tx是一个数。相加的那种也可以转置，就是每一项分别转置再相加。

然后，Clifford algebra上任意元素x的Q，定义为Q(x)= x^tx的常数项。这个应该也等于每一个纯乘法项的Q再相加。

内乘也可以从V上扩展到Clifford algebra上。

参见Geometric_algebra#Extensions_of_the_inner_and_exterior_products 上面是的第三种内积定义*.

[FoxMe]

不错，Q(xy)=Q(x)Q(y),满足norm的乘性。

[TheMatrix]

参见Geometric_algebra#Extensions_of_the_inner_and_exterior_products 上面是的第三种内积定义*.

嗯，看来内积的扩展确实不止一种，而且不能说哪种是canonical的。

[TheMatrix]

不错，Q(xy)=Q(x)Q(y),满足norm的乘性。

norm应该有乘性吗？