Re: 圆锥曲线与齐次方程
发表于 : 2023年 2月 23日 16:28
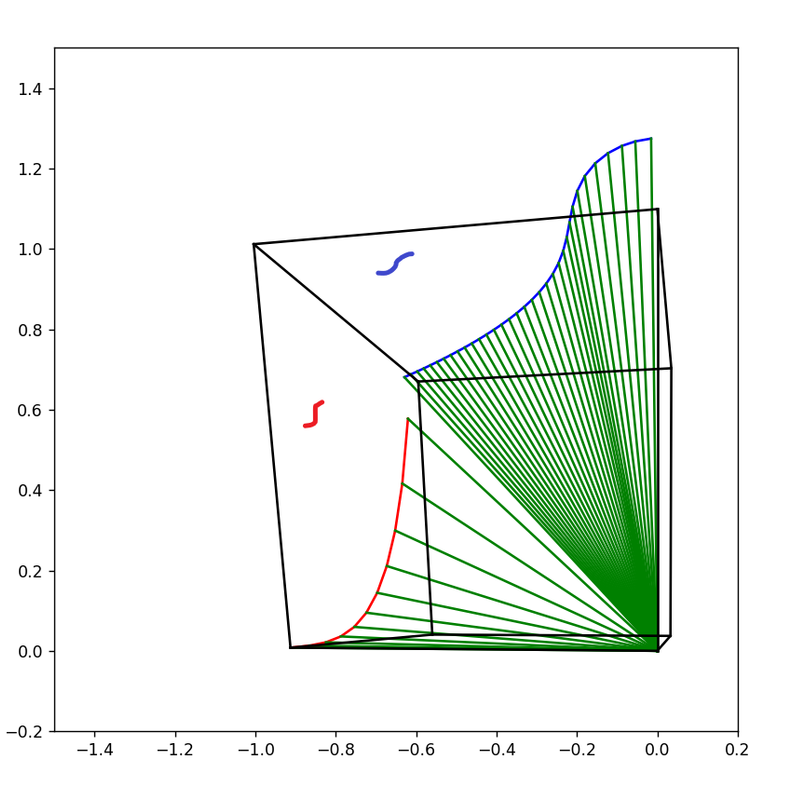
这张好像更清楚一些。观察距离拉远一些,视平面上放大:TheMatrix 写了: 2023年 2月 25日 17:45 上面这张是把z方向放大5倍的。可能没有必要。下面这一张图z没有放大。观察点选在z=1平面的上方,坐标大概在(x=5,y=-1,z=5)附近。图上的坐标没有什么意义,是视平面的二维坐标。
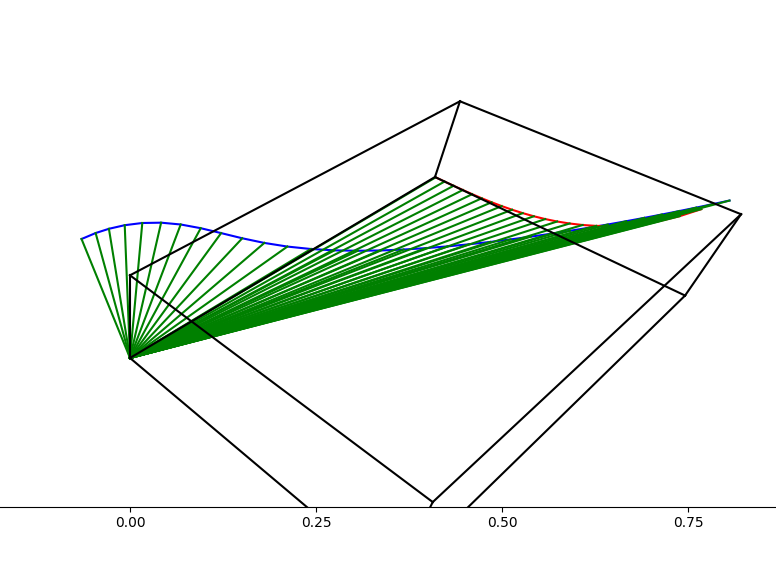
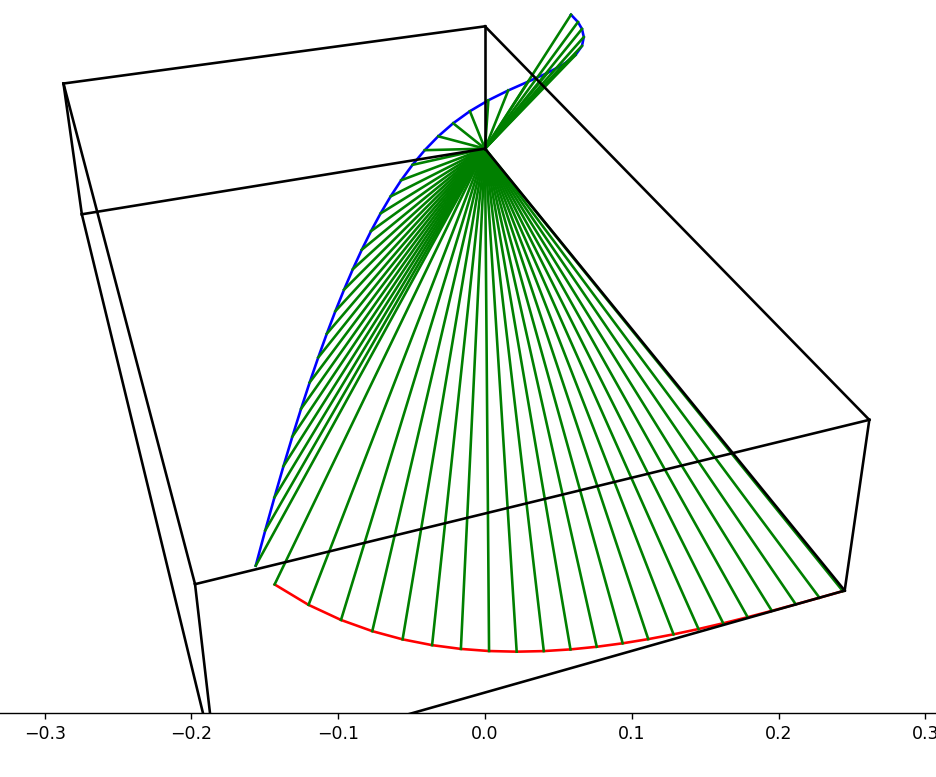
对。就是这样的东西。没有实物真的很难形象化,这还是直纹面,要是一般曲面就更难了。而还是能嵌入三维中的曲面,不能嵌入了就更难了。
直线拉的都是双曲面。比如:z=xy.
这是二次的,还有三次的。比如