新未名空间

FGH 写了： 2024年 1月 3日 22:14 我也有一个关于椭圆的疑惑。我可以直观理解椭圆是圆被压扁的结果。
但是如何直观的理解椭圆的两个焦点？
从一个焦点发射的光线经过椭圆反弹必定到达另一个焦点。

我也长期有此疑问

huangchong 写了： 2024年 1月 3日 22:27 我也长期有此疑问

抛物线还平行光都过焦点呢
不是所有这些数学性质都一定有直观解释

因为圆锥的"边"是直的，所以是线性的。
所以变化的速率是一样的。
同理，切圆柱也是椭圆。

huangchong 写了： 2024年 1月 3日 13:04 此帖转自 翻墙五毛 在 军事天地（Military） 的帖子：如何直观的理解圆锥的切面是个椭圆？

知道孔乙己们又要掉书袋了：”不只是椭圆，还有正圆，抛物线，双曲线。”你妈，这里问的只是椭圆。

圆柱斜着切一刀，切出个椭圆很好理解，符合直觉，因为圆柱两头一样粗。圆锥一头尖一头粗，为啥切出来也是个椭圆？按照直觉，不应该是像鸡蛋一样一头大一头小吗？不要扯什么椭圆函数xy，这里讨论的是直觉

FGH 写了： 2024年 1月 3日 22:14 我也有一个关于椭圆的疑惑。我可以直观理解椭圆是圆被压扁的结果。
但是如何直观的理解椭圆的两个焦点？
从一个焦点发射的光线经过椭圆反弹必定到达另一个焦点。

我来试着通过微积分思想“直观”解释一下，不过可能又变成“数学”了。

你说的“从一个焦点发射的光线经过椭圆反弹必定到达另一个焦点”，就体现在下图中的alpha₁ = alpha₂里面


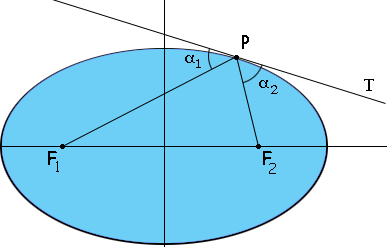
但是为什么必须有alpha₁ = alpha₂呢？网上没找到最恰当的图，就用下面这个凑合吧

为了方便打字，记F1=A，F2=B，PT1=C，PT2=D，PT3=E，并假设CDE之间无穷靠近（微积分思想，呵呵），所以线段距离|CD|和|DE|无穷小。另外记角CDA=角DEA为x，记角BCD=角BDE为y，（几乎）相等是因为|CD|和|DE|无穷小。

从D移动到E，我们得到|AE|-|AD| = |DE| cos(x)；同理，|BD|-|BE| = |DE| cos(y)；这里用到微积分思想，大家拿三角形ADE和BDE比划一下就出来了，注意这两个三角形在A点和B点处的角无穷小，这样在考虑|AE|-|AD|和|BD|-|BE|时能凑出“几乎”直角三角形，细节我就留给大家了。

但是，由于椭圆的定义，|AE|-|AD| = |BD|-|BE|，所以得到|DE| cos(x) = |DE| cos(y)，然后得到x=y，也就是第一个图中的alpha₁ = alpha₂。

直观上说，就是只有时刻保持x=y，才能确保 |AD| + |BD| 是定值。

YWY 写了： 2024年 1月 4日 00:01 我来试着通过微积分思想“直观”解释一下，不过可能又变成“数学”了。

你说的“从一个焦点发射的光线经过椭圆反弹必定到达另一个焦点”，就体现在下图中的alpha₁ = alpha₂里面


但是为什么必须有alpha₁ = alpha₂呢？网上没找到最恰当的图，就用下面这个凑合吧

为了方便打字，记F1=A，F2=B，PT1=C，PT2=D，PT3=E，并假设CDE之间无穷靠近（微积分思想，呵呵），所以线段距离|CD|和|DE|无穷小。另外记角CDA=角DEA为x，记角BCD=角BDE为y，（几乎）相等是因为|CD|和|DE|无穷小。

从D移动到E，我们得到|AE|-|AD| = |DE| cos(x)；同理，|BD|-|BE| = |DE| cos(y)；这里用到微积分思想，大家拿三角形ADE和BDE比划一下就出来了，注意这两个三角形在A点和B点处的角无穷小，这样在考虑|AE|-|AD|和|BD|-|BE|时能凑出“几乎”直角三角形，细节我就留给大家了。

但是，由于椭圆的定义，|AE|-|AD| = |BD|-|BE|，所以得到|DE| cos(x) = |DE| cos(y)，然后得到x=y，也就是第一个图中的alpha₁ = alpha₂。

直观上说，就是只有时刻保持x=y，才能确保 |AD| + |BD| 是定值。

从波动光学看，AD+BD是定值就是说从焦点到焦点，不管从哪条路走，光程一样；
从几何光学看，x=y就是反射定律，光线入射和出射角一样。

你的分析就说明了二者微观上是怎么一致起来的。

设XO交上切圆于P，那么XA=XP，
这个太厉害了。专门画了一下切面才转过劲来。
你们一眼就看懂的好sharp

bihai 写了： 2024年 1月 3日 20:06

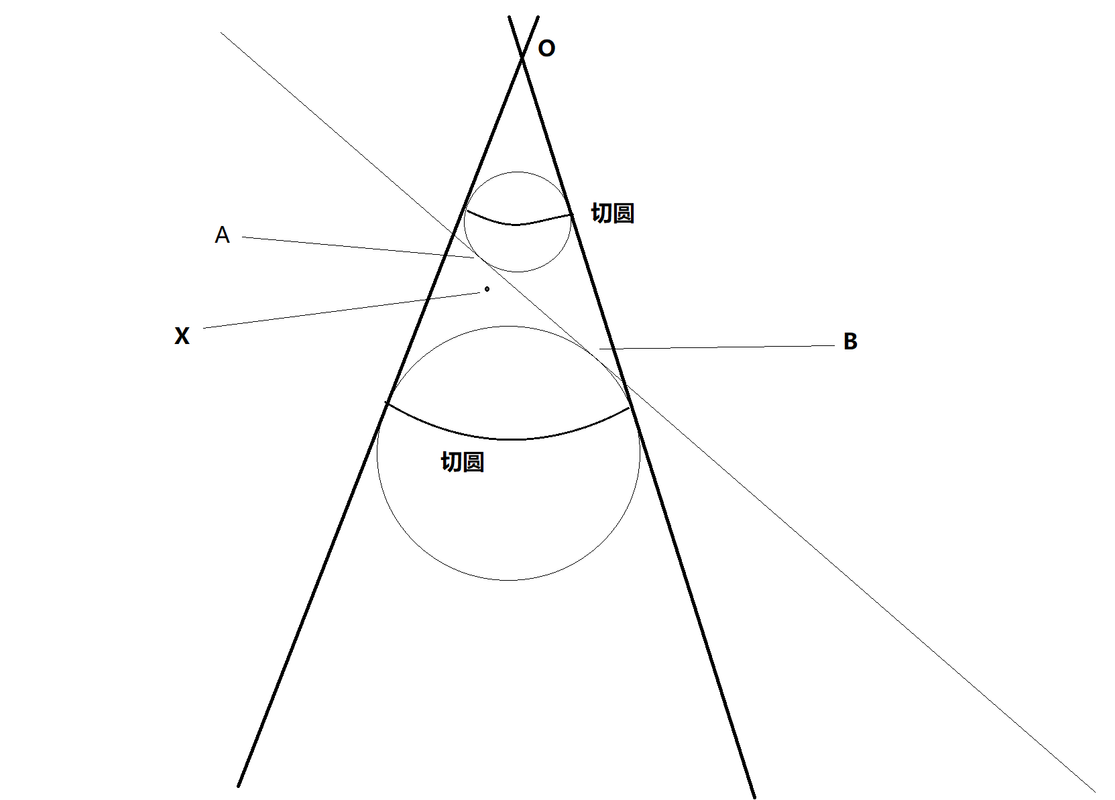
这个图，圆锥顶点是O，平面交圆锥是一个封闭曲线，假设上面有一个点X。下面证明X到两个顶点距离之和为定长。


在圆锥内会有一个内切圆，和圆锥相切（上面的切圆），和平面相切（切点为A）。
在圆锥内会还有一个内切圆，和圆锥相切（下面的切圆），和平面相切（切点为B）。

设XO交上切圆于P，那么XA=XP
设XO交下切圆于Q，那么XB=XQ

则XA + XB＝XP + XQ = PQ

FGH 写了： 2024年 1月 3日 22:14 我也有一个关于椭圆的疑惑。我可以直观理解椭圆是圆被压扁的结果。
但是如何直观的理解椭圆的两个焦点？
从一个焦点发射的光线经过椭圆反弹必定到达另一个焦点。

这是我刚琢磨出来的

假设从半径为1的圆 y方向压扁， 得到的椭圆半长轴还是圆的半径 1 ， 半短轴在1到0之间变化，这个椭圆按比例缩放可以得到任何椭圆



我们知道椭圆半长轴 的2倍长度 等于椭圆上任何一点到两个焦点距离的和

那我们观察“压力”施加的这个点 也就是圆最顶上的这点 还是圆的时候 它到圆心的距离是1, 被往下压的时候 因为到两个焦点距离一样 所以 它到任何一个焦点的距离 等于半长轴的长度，还是1

可以想象 右焦点（黑点） 就是被这根固定长度为1的绿色棍子杵着 在x轴上滑动 就像下面动图里那样。 所以它只好被推着往右走

同理 左焦点被杵着往左走 所以当圆变成椭圆的时候 两个焦点就这么分离了。

而且可以直观看出来 假如我们从一个角度a（偏离圆面法线的角）看半径1的圆圈， 那这个圆圈就变成半长轴为1,半短轴为cos（a） 的椭圆， 而焦点离正中心的距离就是 sin（a）







顺便还发现了一个把desmos变成gif的网站 gifsmos

把单位圆 x^2+y^2=1 绕着 X 轴转动α角， 然后再投影到XY平面， 得到一个椭圆

x^2 + y^2/(cos(alpha))^2 = 1,
其焦点是[+/-sin(α),0]

原来的单位圆上一点 (x,y) 被投影到椭圆上 [x, y cos(α) ]

点［x, y cos(α） ] 到左焦点的距离是

sqrt[(x+sin(α) )^2+(ycos(α))^2]
=sqrt( x^2+2xsin +sin^2 + y^2cos^2)
=sqrt( x^2+2xsin +sin^2 + cos^2-x^2cos^2)
=sqrt( x^2sin^2+2xsin +1)
= 1+xsin（α）

所以[x,ycos(alpha)] 到两个焦点的距离分别是
1+ x sin (alpha)
1- x sin (alpha)
和它的x坐标以及投影倾角成非常简单的关系 而且对于一个给定的椭圆 α是常数 那任何一点到一个焦点的距离 和它的x坐标是简单的线性关系



另外，连焦点，椭圆最顶上的点（0,cos（α））和原点, 得到的角大小就刚好是α。从一个焦点发出的光反射到另一焦点， 此光和反射点法线的夹角此时最大 ，是α

至于 椭圆上 一点到两个焦点的总长为固定值 （以及一开始怎么发现这俩焦点的，显然开普勒那时候就知道这了），除了计算外，不知是否有别的办法

huangchong 写了： 2024年 1月 4日 03:23 把单位圆 x^2+y^2=1 绕着 X 轴转动α角， 然后再投影到XY平面， 得到一个椭圆

x^2 + y^2/(cos(alpha))^2 = 1,
其焦点是[+/-sin(α),0]

原来的单位圆上一点 (x,y) 被投影到椭圆上 [x, y cos(α) ]

点［x, y cos(α） ] 到左焦点的距离是

sqrt[(x+sin(α) )^2+(ycos(α))^2]
=sqrt( x^2+2xsin +sin^2 + y^2cos^2)
=sqrt( x^2+2xsin +sin^2 + cos^2-x^2cos^2)
=sqrt( x^2sin^2+2xsin +1)
= 1+xsin（α）

所以[x,ycos(alpha)] 到两个焦点的距离分别是
1+ x sin (alpha)
1- x sin (alpha)
和它的x坐标以及投影倾角成非常简单的关系 而且对于一个给定的椭圆 α是常数 那任何一点到一个焦点的距离 和它的x坐标是简单的线性关系



另外，连焦点，椭圆最顶上的点（0,cos（α））和原点, 得到的角大小就刚好是α。从一个焦点发出的光反射到另一焦点， 此光和反射点法线的夹角此时最大 ，是α

看来我误解FGH的题意了，我原以为问题是为啥光线从一个焦点发出经反射后必须经过椭圆的另一焦点。原来他问的是怎么直观理解（发现）焦点。我也没啥直观方法，就知道公式a² = b² + c²，其中a和b是椭圆的长短轴，正负c是焦点（位于长轴上）的坐标。所以，在短轴顶点，以长轴为半径做圆，与长轴的交点即为焦点。

3blue1brown讲过这个

翻墙五毛 写了： 2024年 1月 3日 20:58 你妈，问你们如何从直觉理解。一帮孔乙己又开始列方程了。怪不得说是小镇做题家

这么想：平切一刀肯定是圆。角度变一点，那两头就变尖了。变尖的程度和横界面圆的大小无关，只和角度有关。虽然上下两个圆直径不同，但是切的角度是一样的，于是他们变尖的程度是一样的，于是出来一个椭圆。

实在不行就切一万个圆锥，切完就变成直觉了。

MaLaRabbit 写了： 2024年 1月 4日 13:06 变尖的程度和横界面圆的大小无关，只和角度有关。

这个觉得不大保险

直观理解：假设圆锥从无限锐变化到无限钝，任意一个切面的两头都会从接近零度变化到接近正圆，如果是鸡蛋状，大小头至少得出现一次颠倒，这不合理。因此切面两头的变化必定是相等的，切面是个椭圆。

nycstreet 写了： 2024年 1月 4日 20:54 直观理解：假设圆锥从无限锐变化到无限钝，任意一个切面的两头都会从接近零度变化到接近正圆，如果是鸡蛋状，大小头至少得出现一次颠倒，这不合理。因此切面两头的变化必定是相等的，切面是个椭圆。

你这没啥道理。没有理由为什么至少得出现一次颠倒。

巧了，这几天我也在研究椭圆。椭圆里面蕴含着宇宙的大秘密。上一次是牛顿力学的秘密。

verdelite 写了： 2024年 1月 4日 21:43 你这没啥道理。没有理由为什么至少得出现一次颠倒。

是变化的速度不能出现颠倒

nycstreet 写了： 2024年 1月 4日 20:54 直观理解：假设圆锥从无限锐变化到无限钝，任意一个切面的两头都会从接近零度变化到接近正圆，如果是鸡蛋状，大小头至少得出现一次颠倒，这不合理。因此切面两头的变化必定是相等的，切面是个椭圆。

nycstreet 写了： 2024年 1月 4日 22:17 是变化的速度不能出现颠倒

我也没明白你说的颠倒是什么意思。。。

楼主的命题对于椭圆锥、椭圆柱、椭球面也都成立。更一般的就是所有二次曲面。
除了用代数的暴力方法，好像没什么直观。