(转载)如何直观的理解圆锥的切面是个椭圆?
版主: huangchong
-
huangchong(净坛使者)楼主

- 论坛元老

2023-24年度优秀版主 - 帖子互动: 4229
- 帖子: 62128
- 注册时间: 2022年 7月 22日 01:22
#1 (转载)如何直观的理解圆锥的切面是个椭圆?
此帖转自 翻墙五毛 在 军事天地(Military) 的帖子:如何直观的理解圆锥的切面是个椭圆?
知道孔乙己们又要掉书袋了:”不只是椭圆,还有正圆,抛物线,双曲线。”你妈,这里问的只是椭圆。
圆柱斜着切一刀,切出个椭圆很好理解,符合直觉,因为圆柱两头一样粗。圆锥一头尖一头粗,为啥切出来也是个椭圆?按照直觉,不应该是像鸡蛋一样一头大一头小吗?不要扯什么椭圆函数xy,这里讨论的是直觉
知道孔乙己们又要掉书袋了:”不只是椭圆,还有正圆,抛物线,双曲线。”你妈,这里问的只是椭圆。
圆柱斜着切一刀,切出个椭圆很好理解,符合直觉,因为圆柱两头一样粗。圆锥一头尖一头粗,为啥切出来也是个椭圆?按照直觉,不应该是像鸡蛋一样一头大一头小吗?不要扯什么椭圆函数xy,这里讨论的是直觉
#2 Re: (转载)如何直观的理解圆锥的切面是个椭圆?
我也曾有这个疑问。我也没有直观的理解。我最终选择相信xy方程。哪位能给出直观解释就是造福术版(人类)
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
#3 Re: (转载)如何直观的理解圆锥的切面是个椭圆?
一个内切球,一个外切球,两个球与平面的切点为焦点,在圆锥法线方向两个球的切圆距离为定长。则到两个顶点的距离之和为定长,椭圆。huangchong 写了: 2024年 1月 3日 13:04 此帖转自 翻墙五毛 在 军事天地(Military) 的帖子:如何直观的理解圆锥的切面是个椭圆?
知道孔乙己们又要掉书袋了:”不只是椭圆,还有正圆,抛物线,双曲线。”你妈,这里问的只是椭圆。
圆柱斜着切一刀,切出个椭圆很好理解,符合直觉,因为圆柱两头一样粗。圆锥一头尖一头粗,为啥切出来也是个椭圆?按照直觉,不应该是像鸡蛋一样一头大一头小吗?不要扯什么椭圆函数xy,这里讨论的是直觉
-
huangchong(净坛使者)楼主

- 论坛元老

2023-24年度优秀版主 - 帖子互动: 4229
- 帖子: 62128
- 注册时间: 2022年 7月 22日 01:22
-
laodongzhe18(组长)

- 论坛元老

- 帖子互动: 1416
- 帖子: 34447
- 注册时间: 2022年 7月 26日 09:36
#5 Re: (转载)如何直观的理解圆锥的切面是个椭圆?
一个圆锥,如果去掉尖,在仿射几何里一样是个圆柱,而且形变只是一个Z坐标变量。一个平面切过圆柱,Z坐标被消去,所以形变消失,XY平面一样是不变量,即椭圆。这个是解释,不是严格证明。
应运而生 在劫难逃
#7 Re: (转载)如何直观的理解圆锥的切面是个椭圆?
用xyz解方程的话,直接把平面z = ax + by带入圆锥z2 = cx2 + cy2 就行了。laodongzhe18 写了: 2024年 1月 3日 19:02 一个圆锥,如果去掉尖,在仿射几何里一样是个圆柱,而且形变只是一个Z坐标变量。一个平面切过圆柱,Z坐标被消去,所以形变消失,XY平面一样是不变量,即椭圆。这个是解释,不是严格证明。
这里我们是想找到(更加)直观的理解。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
laodongzhe18(组长)

- 论坛元老

- 帖子互动: 1416
- 帖子: 34447
- 注册时间: 2022年 7月 26日 09:36
-
laodongzhe18(组长)

- 论坛元老

- 帖子互动: 1416
- 帖子: 34447
- 注册时间: 2022年 7月 26日 09:36
#11 Re: (转载)如何直观的理解圆锥的切面是个椭圆?
我提个思路, 能不能证明切面以某轴对称? 对称的话除了圆就是椭圆
huangchong 写了: 2024年 1月 3日 13:04 此帖转自 翻墙五毛 在 军事天地(Military) 的帖子:如何直观的理解圆锥的切面是个椭圆?
知道孔乙己们又要掉书袋了:”不只是椭圆,还有正圆,抛物线,双曲线。”你妈,这里问的只是椭圆。
圆柱斜着切一刀,切出个椭圆很好理解,符合直觉,因为圆柱两头一样粗。圆锥一头尖一头粗,为啥切出来也是个椭圆?按照直觉,不应该是像鸡蛋一样一头大一头小吗?不要扯什么椭圆函数xy,这里讨论的是直觉
#15 Re: (转载)如何直观的理解圆锥的切面是个椭圆?
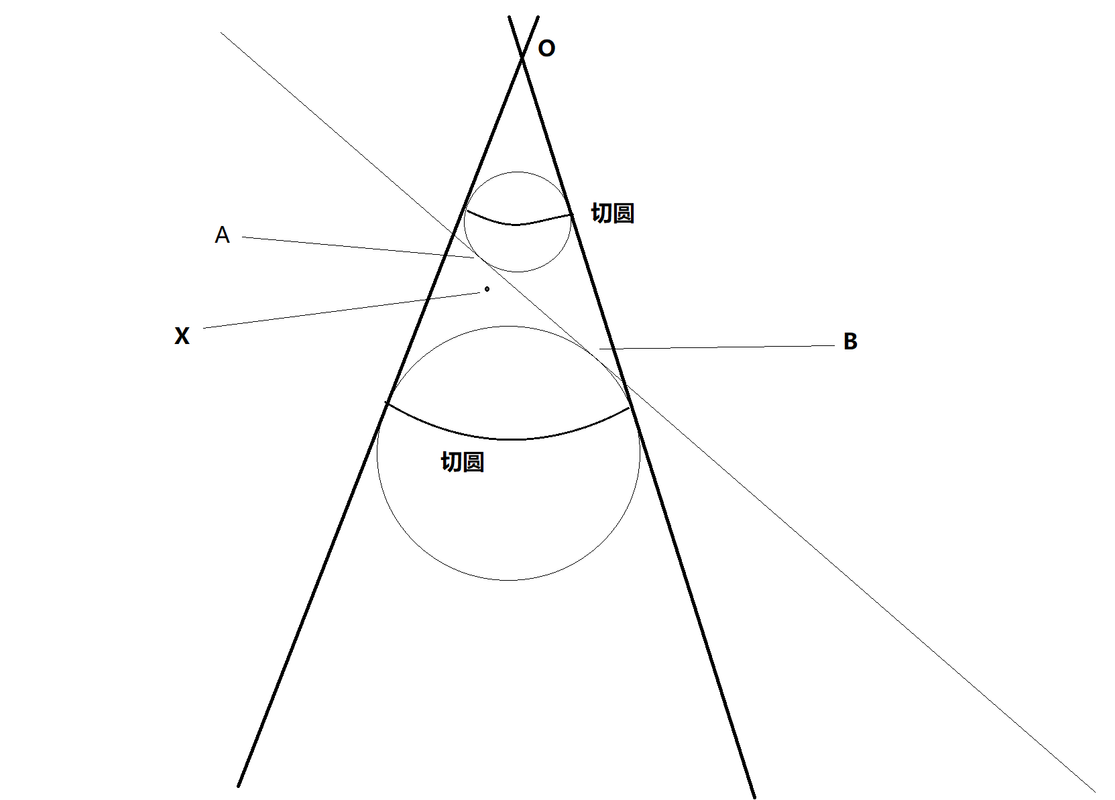
这个图,圆锥顶点是O,平面交圆锥是一个封闭曲线,假设上面有一个点X。下面证明X到两个顶点距离之和为定长。
在圆锥内会有一个内切圆,和圆锥相切(上面的切圆),和平面相切(切点为A)。
在圆锥内会还有一个内切圆,和圆锥相切(下面的切圆),和平面相切(切点为B)。
设XO交上切圆于P,那么XA=XP
设XO交下切圆于Q,那么XB=XQ
则XA + XB=XP + XQ = PQ
+10.00 积分 [版主 huangchong 发放的奖励]
x1


#16 Re: (转载)如何直观的理解圆锥的切面是个椭圆?
谢!厉害!学习了。bihai 写了: 2024年 1月 3日 20:06
这个图,圆锥顶点是O,平面交圆锥是一个封闭曲线,假设上面有一个点X。下面证明X到两个顶点距离之和为定长。
在圆锥内会有一个内切圆,和圆锥相切(上面的切圆),和平面相切(切点为A)。
在圆锥内会还有一个内切圆,和圆锥相切(下面的切圆),和平面相切(切点为B)。
设XO交上切圆于P,那么XA=XP
设XO交下切圆于Q,那么XB=XQ
则XA + XB=XP + XQ = PQ
PQ的长度和点X无关(只要X在交叉曲线上),定长。
别介意啊,我纠正你上面一个术语:OX那条线好像叫圆锥的母线,不是法线(法线一般指垂直于曲面的直线)。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
laodongzhe18(组长)

- 论坛元老

- 帖子互动: 1416
- 帖子: 34447
- 注册时间: 2022年 7月 26日 09:36
#20 Re: (转载)如何直观的理解圆锥的切面是个椭圆?
你把切出来的椭圆和圆锥高线比,huangchong 写了: 2024年 1月 3日 13:04 此帖转自 翻墙五毛 在 军事天地(Military) 的帖子:如何直观的理解圆锥的切面是个椭圆?
知道孔乙己们又要掉书袋了:”不只是椭圆,还有正圆,抛物线,双曲线。”你妈,这里问的只是椭圆。
圆柱斜着切一刀,切出个椭圆很好理解,符合直觉,因为圆柱两头一样粗。圆锥一头尖一头粗,为啥切出来也是个椭圆?按照直觉,不应该是像鸡蛋一样一头大一头小吗?不要扯什么椭圆函数xy,这里讨论的是直觉
确实是一头大一头小
但高线和椭圆相交不在椭圆中点,
所以就算一头大一头小也不影响椭圆对称
#24 Re: (转载)如何直观的理解圆锥的切面是个椭圆?
我也有一个关于椭圆的疑惑。我可以直观理解椭圆是圆被压扁的结果。
但是如何直观的理解椭圆的两个焦点?
从一个焦点发射的光线经过椭圆反弹必定到达另一个焦点。
但是如何直观的理解椭圆的两个焦点?
从一个焦点发射的光线经过椭圆反弹必定到达另一个焦点。
-
huangchong(净坛使者)楼主

- 论坛元老

2023-24年度优秀版主 - 帖子互动: 4229
- 帖子: 62128
- 注册时间: 2022年 7月 22日 01:22
#25 Re: (转载)如何直观的理解圆锥的切面是个椭圆?
厉害厉害 非常精彩bihai 写了: 2024年 1月 3日 20:06
这个图,圆锥顶点是O,平面交圆锥是一个封闭曲线,假设上面有一个点X。下面证明X到两个顶点距离之和为定长。
在圆锥内会有一个内切圆,和圆锥相切(上面的切圆),和平面相切(切点为A)。
在圆锥内会还有一个内切圆,和圆锥相切(下面的切圆),和平面相切(切点为B)。
设XO交上切圆于P,那么XA=XP
设XO交下切圆于Q,那么XB=XQ
则XA + XB=XP + XQ = PQ




