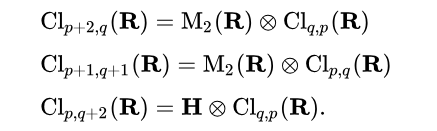Clifford Algebra

[TheMatrix]

n=2
有三种情况：
p=2,q=0，也就是signature(++)，Cl(2,0).
p=1,q=1，也就是signature(+-)，Cl(1,1).
p=0,q=2，也就是signature(--)，Cl(0,2).

p=0,q=2，也就是signature(--)，Cl(0,2).

e₁²=e₂²=-1

(e₁e₂)²=...=-1 也是负的。

也就是Cl(0,2) 四维线性空间的4个生成元 {1,e₁,e₂,e₁e₂}中，有3个平方为负。

那就是quaternion了：
{e₁,e₂,e₁e₂} <--> {i,j,k}。

[TheMatrix]

n=3
p=3,q=0, signature (+++), Cl(3,0)
p=2,q=1, signature (++-), Cl(2,1)
p=1,q=2, signature (+--), Cl(1,2)
p=0,q=3, signature (---), Cl(0,3)

[TheMatrix]

n=3
p=3,q=0, signature (+++), Cl(3,0)
p=2,q=1, signature (++-), Cl(2,1)
p=1,q=2, signature (+--), Cl(1,2)
p=0,q=3, signature (---), Cl(0,3)

n=3
p=3,q=0, signature (+++), Cl(3,0)

这个是3个algebra生成元e₁²=e₂²=e₃²=1
线性空间生成元的话，除了1还有
e₁e₂,e₂e₃,e₃e₁,
e₁e₂e₃,

8维的algebra有哪些？
R⁸
C⁴
H²
M₂(R)⊗C=M₂(C)
M₂(R)⊗R²=M₂(R²)=M₂(R)²
H⊕C²
H⊕M₂(R)
...

太多了，这样找可能不行。

还可以从Cl(3,0)的表示论出发。最基本的，regular representation，Cl(3,0)在自身上的表示。也就是一个8维的表示。然后看看能不能简化。

最后，还有这么一个公式：



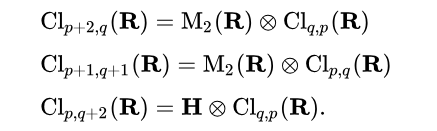
根据这个公式，
Cl(3,0)=Cl(2,0)⊗Cl(0,1)=M₂(R)⊗C=M₂(C)

很好用。但是没有给出具体的映射：
ɸ: Cl(3,0) --> M₂(C)

[TheMatrix]

n=3
p=3,q=0, signature (+++), Cl(3,0)

根据这个公式，
Cl(3,0)=Cl(2,0)⊗Cl(0,1)=M₂(R)⊗C=M₂(C)

很好用。但是没有给出具体的映射：
ɸ: Cl(3,0) --> M₂(C)

这个公式肯定是对的。

看它的结果也是有点意思的。

M₂(C)，看起来像是一个Clifford algebra over the complex。

Cl(2,C)，也就是一个vector space over the complex，2 dim。两个algebra生成元 e₁,e₂。这里不用写signature了，因为在complex vector space上不需要signature的概念了。可以统一写成 e₁²=e₂²=1。

那么按照Cl(2,0)的办法，它的Clifford algebra是M₂，只不过是complex-valued。所以就是M₂(C)。

这说明什么？这说明 Cl(3,0) = Cl(2,C)。一个real Clifford algebra可以等于一个complex Clifford algebra。

[TheMatrix]

这个公式肯定是对的。

看它的结果也是有点意思的。

M₂(C)，看起来像是一个Clifford algebra over the complex。

Cl(2,C)，也就是一个vector space over the complex，2 dim。两个algebra生成元 e₁,e₂。这里不用写signature了，因为在complex vector space上不需要signature的概念了。可以统一写成 e₁²=e₂²=1。

那么按照Cl(2,0)的办法，它的Clifford algebra是M₂，只不过是complex-valued。所以就是M₂(C)。

这说明什么？这说明 Cl(3,0) = Cl(2,C)。一个real Clifford algebra可以等于一个complex Clifford algebra。

从这个公式的结果也可以凑出这个映射：

ɸ: Cl(3,0) --> M₂(C)
ɸ(e₁) = diag(1,-1)
ɸ(e₂) = [[0,1],[1,0]]
这个和Cl(2,0)或者Cl(2,C)是一样的。

最后一个ɸ(e₃)一定和i有关，因为要得到complex value entry。

试一下，发现
ɸ(e₃) = [[0,i],[-i,0]]。

[TheMatrix]

从这个公式的结果也可以凑出这个映射：

ɸ: Cl(3,0) --> M₂(C)
ɸ(e₁) = diag(1,-1)
ɸ(e₂) = [[0,1],[1,0]]
这个和Cl(2,0)或者Cl(2,C)是一样的。

最后一个ɸ(e₃)一定和i有关，因为要得到complex value entry。

试一下，发现
ɸ(e₃) = [[0,i],[-i,0]]。

哦。这就是三个Pauli matrix啊！

顺序有点变化。

[TheMatrix]

最后，还有这么一个公式：

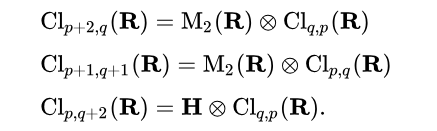
还在想这三个公式的证明。因为证明了才能知道基矢量具体映射到什么matrix上。

感觉这几个公式还是可以理解的。

比如 Cl(p+2,q) = Cl(2,0)⊗Cl(q,p)

也就是一个real vector space有p+2个正的基矢量，q个负的基矢量。它的Clifford algebra等于一个2X2的矩阵，但是其系数可以取自另一个Clifford algebra，这个系数Clifford algebra的基矢量基本上是原来基矢量的正负变号。不知道为什么会变号。

Cl(p+2,q)中的一个元素，类似于一个多项式，每一项都有一些变量，是由基矢量的符号组成。如果选定其中的两个正的基矢量，比如说e₁,e₂，只把这两个作为变量，其余的基矢量都看成是系数的话，那么这是一个只有两个正基矢量的Clifford algebra，但是系数空间变成了由其他基矢量构成的代数。这和公式右边的表达式吻合。

[TheMatrix]

还在想这三个公式的证明。因为证明了才能知道基矢量具体映射到什么matrix上。

感觉这几个公式还是可以理解的。

比如 Cl(p+2,q) = Cl(2,0)⊗Cl(q,p)

也就是一个real vector space有p+2个正的基矢量，q个负的基矢量。它的Clifford algebra等于一个2X2的矩阵，但是其系数可以取自另一个Clifford algebra，这个系数Clifford algebra的基矢量基本上是原来基矢量的正负变号。不知道为什么会变号。

Cl(p+2,q)中的一个元素，类似于一个多项式，每一项都有一些变量，是由基矢量的符号组成。如果选定其中的两个正的基矢量，比如说e₁,e₂，只把这两个作为变量，其余的基矢量都看成是系数的话，那么这是一个只有两个正基矢量的Clifford algebra，但是系数空间变成了由其他基矢量构成的代数。这和公式右边的表达式吻合。

知道了。应该直接从基矢量tensor product方向上考虑。

Cl(2,0)有两个正的基矢量e₁,e₂。那么定义e₃=e₁e₂，发现e₃²=-1，而且e₃和e₁,e₂换序都变号。

Cl(q,p)有q个正的基矢量，f₁,...，和p个负的基矢量，g₁,...

那么Cl(2,0)⊗Cl(q,p)首先有
e₁⊗1
e₂⊗1
两个正的基矢量：
(e₁⊗1)(e₁⊗1)=e₁²⊗1=1⊗1=1
tensor符号左边的1是Cl(2,0)中的1，tensor右边的1是Cl(q,p)中的1。
而最后的1是Cl(2,0)⊗Cl(q,p)的1.

然后
e₃⊗g₁是一个正的基矢量：
(e₃⊗g₁)(e₃⊗g₁)
=e₃²⊗g₁²
=-1⊗-1
=1⊗1
=1

e₃⊗f₁是一个负的基矢量：推理相似。

这样又有了p个正的基矢量和q个负的基矢量。

而且这些基矢量都满足换序变号：
(e₃⊗g₁)(e₃⊗f₁)
=e₃²⊗g₁f₁

(e₃⊗f₁)(e₃⊗g₁)
=e₃²⊗f₁g₁
=-e₃²⊗g₁f₁

...

所以Cl(2,0)⊗Cl(q,p)总共有p+2个正的基矢量，和q个负的基矢量，它们都满足换序变号，那么它必然是Cl(p+2,q)。

[TheMatrix]

知道了。应该直接从基矢量tensor product方向上考虑。

Cl(2,0)有两个正的基矢量e₁,e₂。那么定义e₃=e₁e₂，发现e₃²=-1，而且e₃和e₁,e₂换序都变号。

Cl(q,p)有q个正的基矢量，f₁,...，和p个负的基矢量，g₁,...

那么Cl(2,0)⊗Cl(q,p)首先有
e₁⊗1
e₂⊗1
两个正的基矢量：
(e₁⊗1)(e₁⊗1)=e₁²⊗1=1⊗1=1
tensor符号左边的1是Cl(2,0)中的1，tensor右边的1是Cl(q,p)中的1。
而最后的1是Cl(2,0)⊗Cl(q,p)的1.

然后
e₃⊗g₁是一个正的基矢量：
(e₃⊗g₁)(e₃⊗g₁)
=e₃²⊗g₁²
=-1⊗-1
=1⊗1
=1

e₃⊗f₁是一个负的基矢量：推理相似。

这样又有了p个正的基矢量和q个负的基矢量。

而且这些基矢量都满足换序变号：
(e₃⊗g₁)(e₃⊗f₁)
=e₃²⊗g₁f₁

(e₃⊗f₁)(e₃⊗g₁)
=e₃²⊗f₁g₁
=-e₃²⊗g₁f₁

...

所以Cl(2,0)⊗Cl(q,p)总共有p+2个正的基矢量，和q个负的基矢量，它们都满足换序变号，那么它必然是Cl(p+2,q)。

另外两个公式也可以类似证明：
Cl(p,q+2) = Cl(0,2)⊗Cl(q,p)
Cl(p+1,q+1)=Cl(1,1)⊗Cl(p,q)

而且基矢量也都明确的给出了。

从tensor product作为换系数的方向考虑，不容易走通，因为是非交换的，比较麻烦。

[TheMatrix]

另外两个公式也可以类似证明：
Cl(p,q+2) = Cl(0,2)⊗Cl(q,p)
Cl(p+1,q+1)=Cl(1,1)⊗Cl(p,q)

而且基矢量也都明确的给出了。

从tensor product作为换系数的方向考虑，不容易走通，因为是非交换的，比较麻烦。

做个练习：
Cl(1,3)=Cl(0,2)⊗Cl(1,1)

Cl(0,2)=H，有两个负基矢量i和j，另一个ij=k。

Cl(1,1)=M₂(R)，有一个正基矢量e₁=diag(1,-1)，一个负基矢量e₂=reverse diag(1,-1)，另一个e₃=e₁e₂=reverse diag(1,1)。

那么Cl(0,2)⊗Cl(1,1)有四个基矢量：
i⊗1 -- 1是Cl(1,1)中的1，也就是2X2单位矩阵 I。
j⊗1
k⊗e₁
k⊗e₂

可以写成2X2矩阵的形式，但是entry为H - quaternion：
diag(i,i)
diag(j,j)
diag(k,-k)
reverse diag(k,-k)

这是一种写法。

还可以反过来：
Cl(1,3)=Cl(1,1)⊗Cl(0,2)

有另外四个基矢量：
e₁⊗1 -- 1是H中的1，也就是quaternion中的1.
e₂⊗1
e₃⊗i -- i是H中的i
e₃⊗j

也可以写成2X2矩阵的形式，entry还是H：
diag(1,-1)
reverse diag(1,-1)
reverse diag(i,i)
reverse diag(j,j)

[TheMatrix]

另外两个公式也可以类似证明：
Cl(p,q+2) = Cl(0,2)⊗Cl(q,p)
Cl(p+1,q+1)=Cl(1,1)⊗Cl(p,q)

而且基矢量也都明确的给出了。

从tensor product作为换系数的方向考虑，不容易走通，因为是非交换的，比较麻烦。

再做个练习：
Cl(3,1)=Cl(2,0)⊗Cl(1,1)

Cl(2,0)=M₂(R)，有两个正的基矢量，e₁=diag(1,-1)，e₂=reverse diag(1,1)。第三个e₃=e₁e₂=reverse diag(1,-1)。

Cl(1,1)=M₂(R)，对，它们是一样的，但是基矢不同。有一个正基矢量，e₁=diag(1,-1)，一个负基矢量e₂=reverse diag(1,-1)。第三个e₃=e₁e₂=reverse diag(1,1)。它和前面那个就是e₂,e₃的换序。

Cl(2,0)⊗Cl(1,1)的基矢量有4个：
e₁⊗1 -- 1是Cl(1,1)中的1，也就是2X2 单位矩阵 I.
e₂⊗1
e₃⊗e₁ --左边的e₃是Cl(2,0)中的e₃，右边的e₁是Cl(1,1)中的e₁.
e₃⊗e₂

它们都是2X2 matrix tensor 另一个2X2 matrix，可以展开成4X4 matrix。可以把右边的代入左边的，也可以把左边的代入右边的，但是必须先固定一种代入方法。

还可以反过来：
Cl(3,1)=Cl(1,1)⊗Cl(2,0)

[TheMatrix]

再做个练习：
Cl(3,1)=Cl(2,0)⊗Cl(1,1)

Cl(2,0)=M₂(R)，有两个正的基矢量，e₁=diag(1,-1)，e₂=reverse diag(1,1)。第三个e₃=e₁e₂=reverse diag(1,-1)。

Cl(1,1)=M₂(R)，对，它们是一样的，但是基矢不同。有一个正基矢量，e₁=diag(1,-1)，一个负基矢量e₂=reverse diag(1,-1)。第三个e₃=e₁e₂=reverse diag(1,1)。它和前面那个就是e₂,e₃的换序。

Cl(2,0)⊗Cl(1,1)的基矢量有4个：
e₁⊗1 -- 1是Cl(1,1)中的1，也就是2X2 单位矩阵 I.
e₂⊗1
e₃⊗e₁ --左边的e₃是Cl(2,0)中的e₃，右边的e₁是Cl(1,1)中的e₁.
e₃⊗e₂

它们都是2X2 matrix tensor 另一个2X2 matrix，可以展开成4X4 matrix。可以把右边的代入左边的，也可以把左边的代入右边的，但是必须先固定一种代入方法。

还可以反过来：
Cl(3,1)=Cl(1,1)⊗Cl(2,0)

这样写出来的四个基矢量的矩阵都是4X4实数矩阵。不涉及complex number。

可以complexify，也就是Cl(3,1)⊗C，变成4X4 complex matrix。同时它也是4维复向量空间的Clifford algebra。但是4个基矢量可以不变。仍然是实数entry。

看来γ matrix可以不唯一啊。

[TheMatrix]

做个练习：
Cl(1,3)=Cl(0,2)⊗Cl(1,1)

Cl(0,2)=H，有两个负基矢量i和j，另一个ij=k。

Cl(1,1)=M₂(R)，有一个正基矢量e₁=diag(1,-1)，一个负基矢量e₂=reverse diag(1,-1)，另一个e₃=e₁e₂=reverse diag(1,1)。

那么Cl(0,2)⊗Cl(1,1)有四个基矢量：
i⊗1 -- 1是Cl(1,1)中的1，也就是2X2单位矩阵 I。
j⊗1
k⊗e₁
k⊗e₂

可以写成2X2矩阵的形式，但是entry为H - quaternion：
diag(i,i)
diag(j,j)
diag(k,-k)
reverse diag(k,-k)

这是一种写法。

还可以反过来：
Cl(1,3)=Cl(1,1)⊗Cl(0,2)

有另外四个基矢量：
e₁⊗1 -- 1是H中的1，也就是quaternion中的1.
e₂⊗1
e₃⊗i -- i是H中的i
e₃⊗j

也可以写成2X2矩阵的形式，entry还是H：
diag(1,-1)
reverse diag(1,-1)
reverse diag(i,i)
reverse diag(j,j)

Dirac 4个γ matrix是：

γ⁰= diag(1,1,-1,-1)

γⁱ=[[0,σⁱ],[-σⁱ,0]]

其中σ是Pauli matrix，2X2：

σ¹=[[0,1],[1,0]]
σ²=[[0,-i],[i,0]]
σ³=[[1,0],[0,-1]]

都是4X4 complex matrix，说明这是complex Clifford algebra，Cl(4,C)。

其中
γ⁰γ⁰=I
γ¹γ¹=-I
γ²γ²=-I
γ³γ³=-I
说明这是从Cl(1,3)演变过来的？

但是我得到的Cl(1,3)都是2X2 quaternion matrix。这两个之间的关系还没搞清。

[TheMatrix]

Dirac 4个γ matrix是：

γ⁰= diag(1,1,-1,-1)

γⁱ=[[0,σⁱ],[-σⁱ,0]]

其中σ是Pauli matrix，2X2：

σ¹=[[0,1],[1,0]]
σ²=[[0,-i],[i,0]]
σ³=[[1,0],[0,-1]]

都是4X4 complex matrix，说明这是complex Clifford algebra，Cl(4,C)。

其中
γ⁰γ⁰=I
γ¹γ¹=-I
γ²γ²=-I
γ³γ³=-I
说明这是从Cl(1,3)演变过来的？

但是我得到的Cl(1,3)都是2X2 quaternion matrix。这两个之间的关系还没搞清。

看来γ matrix并不唯一。

如果γ matrix只是要求
1，γ₀,γ₁,γ₂,γ₃平方等于±1，
2，它们之间两两换序变号，
的话，那么有很多种方式。甚至只用实matrix就可以。

如果要求1改为γ₀²=1，γ₁²⁼γ₂²=γ₃²=-1，也就是按照Cl(1,3)的方式来，的话，也有不止一种方式。

[TheMatrix]

Dirac 4个γ matrix是：

γ⁰= diag(1,1,-1,-1)

γⁱ=[[0,σⁱ],[-σⁱ,0]]

其中σ是Pauli matrix，2X2：

σ¹=[[0,1],[1,0]]
σ²=[[0,-i],[i,0]]
σ³=[[1,0],[0,-1]]

都是4X4 complex matrix，说明这是complex Clifford algebra，Cl(4,C)。

其中
γ⁰γ⁰=I
γ¹γ¹=-I
γ²γ²=-I
γ³γ³=-I
说明这是从Cl(1,3)演变过来的？

但是我得到的Cl(1,3)都是2X2 quaternion matrix。这两个之间的关系还没搞清。

H != M₂(R)
但是
H⊗C=M₂(R)⊗C
它们都等于M₂(C)。

而且这个同构有很多种方式，都是对称的。

也就是作为real algebra不同构的两个algebra，complexify之后可以同构。

比如H中有ijk，
C中有i，
M₂(R)中有e₁=diag(1,-1)，e₂=reverse diag(1,1)，e₃=e₁e₂=reverse diag(1,-1)。

那么H⊗C=M₂(R)⊗C之间的一个同构是：
i⊗i --> e₁⊗1 --> diag(1,-1) (in M₂(C))
j⊗i --> e₂⊗1 --> reverse diag(1,1) (in M₂(C))
k⊗i --> e₃⊗-i --> reverse diag(-i,i) (in M₂(C))

哦。这好像就是Pauli matrix啊。

所以Cl(1,3)=M₂(R)⊗H
再complexify
Cl(1,3)⊗C=M₂(R)⊗H⊗C=M₂(R)⊗M₂(C)=M₄(C)
里面可能确实会出现Pauli matrix。。。

[TheMatrix]

H != M₂(R)
但是
H⊗C=M₂(R)⊗C
它们都等于M₂(C)。

而且这个同构有很多种方式，都是对称的。

也就是作为real algebra不同构的两个algebra，complexify之后可以同构。

比如H中有ijk，
C中有i，
M₂(R)中有e₁=diag(1,-1)，e₂=reverse diag(1,1)，e₃=e₁e₂=reverse diag(1,-1)。

那么H⊗C=M₂(R)⊗C之间的一个同构是：
i⊗i --> e₁⊗1 --> diag(1,-1) (in M₂(C))
j⊗i --> e₂⊗1 --> reverse diag(1,1) (in M₂(C))
k⊗i --> e₃⊗-i --> reverse diag(-i,i) (in M₂(C))

哦。这好像就是Pauli matrix啊。

所以Cl(1,3)=M₂(R)⊗H
再complexify
Cl(1,3)⊗C=M₂(R)⊗H⊗C=M₂(R)⊗M₂(C)=M₄(C)
里面可能确实会出现Pauli matrix。。。

知道了。Pauli matrix是这么出现的：

Cl(1,3)⊗C=Cl(1,1)⊗Cl(0,2)⊗C=M₂(R)⊗H⊗C=M₂(R)⊗M₂(C)

M₂(R)有两个基矢量。一个正的：e₁=diag(1,-1)，一个负的：e₂=reverse diag(1,-1)，第三个也是正的：e₃=e₁e₂=reverse diag(1,1)。

H⊗C=M₂(C)也有两个基矢量（但是系数为C）。都是正的：e₁=diag(1,-1)，e₂=reverse diag(1,1)。第三个定义为e₃=-ie₁e₂=reverse diag(-i,i)。

γ matrix这么定义：
in M₂(R)⊗M₂(C)，左边的归左边，右边的归右边：

γ₀=e₁⊗I
γ₁=e₂⊗e₁
γ₂=e₂⊗e₂
γ₃=e₂⊗e₃

tensor右边的e₁,e₂,e₃就是三个Pauli matrix。

这样γ₀是正的，其余三个γ₁,γ₂,γ₃是负的。看起来可以说是从Cl(1,3)出来的。

这就是Dirac的γ matrix。

还可以有其他的方法组合：
e₁⊗I
e₂⊗I
e₃⊗e₁
e₃⊗e₂

每一个基矢量想要正负都可以加一个i来调节。

[Caravel]

知道了。Pauli matrix是这么出现的：

Cl(1,3)⊗C=Cl(1,1)⊗Cl(0,2)⊗C=M₂(R)⊗H⊗C=M₂(R)⊗M₂(C)

M₂(R)有两个基矢量。一个正的：e₁=diag(1,-1)，一个负的：e₂=reverse diag(1,-1)，第三个也是正的：e₃=e₁e₂=reverse diag(1,1)。

H⊗C=M₂(C)也有两个基矢量（但是系数为C）。都是正的：e₁=diag(1,-1)，e₂=reverse diag(1,1)。第三个定义为e₃=-ie₁e₂=reverse diag(-i,i)。

γ matrix这么定义：
in M₂(R)⊗M₂(C)，左边的归左边，右边的归右边：

γ₀=e₁⊗I
γ₁=e₂⊗e₁
γ₂=e₂⊗e₂
γ₃=e₂⊗e₃

tensor右边的e₁,e₂,e₃就是三个Pauli matrix。

这样γ₀是正的，其余三个γ₁,γ₂,γ₃是负的。看起来可以说是从Cl(1,3)出来的。

这就是Dirac的γ matrix。

还可以有其他的方法组合：
e₁⊗I
e₂⊗I
e₃⊗e₁
e₃⊗e₂

每一个基矢量想要正负都可以加一个i来调节。

对， 用Pauli矩阵tensor product就可以得到gamma matrix， 还必须满足反对易关系. clifford algebra可以构造出来高阶的gamma矩阵。

https://sites.science.oregonstate.edu/c ... gamma.html

这个链接里面给出了另外一个表象Weyl representation

[pinfish]

clifford本人的命名就是geometric algerba
一开始本来就是用来研究几何用的，内积外积几何积

Clifford Algebra我学过好几次了。

最早是从纯代数学习，学得有点不明所以。

上次和Caravel以及FoxMe的讨论学到了不少东西，一个是以基矢量的方式表达Clifford algebra的乘法结构，非常具体，非常清楚，也非常具有可计算性。另一个是Clifford algebra对基矢量空间的反射和旋转的作用。这应该也是Clifford algebra得名geometric algebra的原因。

最近一次是学Dirac方程γ matrix。

并没有完全理清，还有一些问题。打算总结一下。

[FoxMe]

赞态度认真

[xexz]

认真、执着。

看看这个是否对你有帮助，https://zhuanlan.zhihu.com/p/338774412


叔瞎说两句，总之，对电磁场中的电子，只考虑物理的话，如果不想要‘带负电荷电子’的‘负概率/负能量’，那么何不试试‘带正电荷电子’的‘正概率/正能量’？

毕竟，如果我们还想舒适的呆在现实世界里，‘正概率/正能量’还是必须的。

没见过‘正电子’呀，找着不就行了。

至于数学，办法总会有的，只要你真找到了‘正电子’（只有电子自旋是已知的物理前提，其他是基于逻辑规律的数学预言），自会有数学大儒来替你辩经的。

FBI个人观点：不是数学专业，似乎没有浪费精力的必要。