如何理论导出电子自旋

[seymour]

While it is impossible to find half spin eigenstates when solving the Schrodinger's equation in R3 using differential equations, half spin naturally arises when solving the rotational problem with raising and lowering operators. The raising operator will take an eigenstate and raise to a different eigenstate with the Lz eigen value increase by hbar. The top state must have its eigenvalue negative of the bottom state, this condition allows any half integer solutions, except it is not possible to write such solutions in R3.
Thus the state can only be written using matrices or simply as alpha and beta.

Schrodinger方程应该是不能导出电子自旋的。

Schrodinger方程里的波函数ψ的值是复数，一个复数，而不是C²或者Cⁿ。所以它不能导出电子自旋。这是我目前的理解。

自旋和旋转有关，旋转是SO(3)，在相对论坐标系下是SO(1,3)。

乍一看，SO(3)可以作用在ψ上，因为 ψ : (t,x,y,z) --> C 也是空间的函数，而SO(3)可以作用在空间(x,y,z)上。但是这个作用必须作用在整个系统上，是所谓的全局对称性。它得到的是系统的角动量，以及角动量的量子化。而不是电子的自旋。

电子自旋是所谓的内禀属性，内禀属性必须反映在 ψ 的函数值上，而不是 ψ 的定义域上。所以必须 ψ : (t,x,y,z) --> C²，或者更高的 Cⁿ，才能得到自旋。C²的话，就可以有SU(2)对称性，SU(2)是SO(3)的double cover，这应该就可以反映自旋了。内禀对称性，到场论中，就过渡到局部对称性。

波函数 ψ : (t,x,y,z) --> C² 的就是Dirac方程。Dirac方程我还不太理解。

但是无论Schrodinger方程还是Dirac方程，都是单系统方程，是从单体到多体这个方向发展上来的。它不是场论方程。

[TheMatrix]

要写出“标准”表示的matrix，就把(e₀,e₁,e₂,e₃)作用在自身上的效果写出来。注意这里的“作用”不是Clifford algebra的相乘，而是“对法平面反射”，也就是v.u=-vuv^-1。

比如
e₀作用在e₁上，考虑e₀的法平面，然后这个平面如何反射e₁，...，得到的结果还是e₁。

用Clifford algebra得到的结果是一样的：
e₀.e₁=-e₀e₁e₀^-1=-e₀e₁e₀=e₀e₀e₁=e₁

这样做发现：
e₀.e₀=-e₀
e₀.e₁=e₁
e₀.e₂=e₂
e₀.e₃=e₃

所以e₀的matrix就是 diag(-1,1,1,1)。

同样，
e₁的matrix是 diag(1,-1,1,1)，
e₂的matrix是 diag(1,1,-1,1)，
e₃的matrix是 diag(1,1,1,-1)，

规律这么简单，是不是做错了？

先接受它。

但是这和Dirac 4个γ matrix不同。

Dirac 4个γ matrix是：

γ⁰= diag(1,1,-1,-1)

γⁱ=[[0,σⁱ],[-σⁱ,0]]

其中σ是Pauli matrix，2X2：

σ¹=[[0,1],[1,0]]
σ²=[[0,-i],[i,0]]
σ³=[[1,0],[0,-1]]

这个确实是错的。最简单的看，这个几个基矢量对应的matrix都是diagonal，这就不对，因为这样乘法就可交换了，而不是变号。

这个错误是从哪来的呢？现在还没想明白。

基矢量对基空间的作用是“关于法平面的反射”，这是一个疑点。

但是，这个作用能否扩展为Clifford algebra在基空间上的表示，这是一个更大的疑点。

查了一下，Minkowski空间，也就是signature (+,-,-,-)的R⁴空间，对应的Clifford algebra是Cl(1,3)，它应该同构于H(2)，也就是2X2 quarternion matrix。这就和Dirac γ matrix对上了。三个Pauli matrix正对应quarternion的i,j,k。

[Caravel]

这个确实是错的。最简单的看，这个几个基矢量对应的matrix都是diagonal，这就不对，因为这样乘法就可交换了，而不是变号。

这个错误是从哪来的呢？现在还没想明白。

基矢量对基空间的作用是“关于法平面的反射”，这是一个疑点。

但是，这个作用能否扩展为Clifford algebra在基空间上的表示，这是一个更大的疑点。

查了一下，Minkowski空间，也就是signature (+,-,-,-)的R⁴空间，对应的Clifford algebra是Cl(1,3)，它应该同构于H(2)，也就是2X2 quarternion matrix。这就和Dirac γ matrix对上了。三个Pauli matrix正对应quarternion的i,j,k。

需要的γ matrix的性质是anti communitive， 这样两个算符叠加，交叉项可以消去，法向量反射是怎么来的？

[TheMatrix]

需要的γ matrix的性质是anti communitive， 这样两个算符叠加，交叉项可以消去，法向量反射是怎么来的？

前段时间和你以及FoxMe讨论Clifford algebra，得到了两个知识：
1，以基矢量的方式表示Clifford algebra的乘法比较好理解。
2，单矢量可以作用在基矢量空间，作用的效果是“对该矢量法平面的反射”，用Clifford algebra的乘法表示就是：v.u=-vuv^-1。而两次反射等于一个旋转。

这两点都是对的。但是我刚刚发现，“对法平面的反射”这个操作不构成Clifford algebra对基矢量空间的action，因为 u.(v.w) != (uv).w。所以这个操作也不构成Clifford algebra在基矢量空间上的表示。差的不多，但是怎么补偿还不清楚。

[Caravel]

前段时间和你以及FoxMe讨论Clifford algebra，得到了两个知识：
1，以基矢量的方式表示Clifford algebra的乘法比较好理解。
2，单矢量可以作用在基矢量空间，作用的效果是“对该矢量法平面的反射”，用Clifford algebra的乘法表示就是：v.u=-vuv^-1。而两次反射等于一个旋转。

这两点都是对的。但是我刚刚发现，“对法平面的反射”这个操作不构成Clifford algebra对基矢量空间的action，因为 u.(v.w) != (uv).w。所以这个操作也不构成Clifford algebra在基矢量空间上的表示。差的不多，但是怎么补偿还不清楚。

这就是求clifford_algebra cl(3,1) matrix representation的问题，说老实话，我也没想明白怎么用clifford glebra系统的得出这些矩阵。历史上，Dirac大功率是通过pauli matrix 凑出来的。

[TheMatrix]

这就是求clifford_algebra cl(3,1) matrix representation的问题，说老实话，我也没想明白怎么用clifford glebra系统的得出这些矩阵。历史上，Dirac大功率是通过pauli matrix 凑出来的。

对。是Cl(3,1)或Cl(1,3)的表示论问题。这两个应该是一样的吧？这两天玩了一下，还没完全搞明白。我觉得可能应该是从各维度代数的分类入手，因为这些都是低维度的，分类应该并不多。

比如4个实数维的代数，只能是几种情况，R⁴, C², H (quarternion), M₂(R) (2X2 matrix with real entry), …

[TheMatrix]

对。是Cl(3,1)或Cl(1,3)的表示论问题。这两个应该是一样的吧？这两天玩了一下，还没完全搞明白。我觉得可能应该是从各维度代数的分类入手，因为这些都是低维度的，分类应该并不多。

比如4个实数维的代数，只能是几种情况，R⁴, C², H (quarternion), M₂(R) (2X2 matrix with real entry), …

Cl(p,q)是signature （p个正，q个负）的metric的实vector space的Clifford algebra。

Cl(0,0)是0 vector space的Clifford algebra，只有1作为生成元，所以等于R。
Cl(1,0)=R²
Cl(0,1)=C
Cl(2,0)=M₂(R)
Cl(1,1)=M₂(R) - 这个和前面一个相等，也就是isomorphic，但是生成元之间要有一个映射。
Cl(0,2)=H - quarternion

这几个是极低维的，直接试探生成元映射就能找到。

比如 Cl(2,0) 的 signature 是 (+,+)，e₁²=e₂²=1, (e₁e₂)²=-1。

它是4维的，试探一下M₂(R)。
1 --> diag(1,1)
e₁ --> diag(1,-1)
e₂ --> [[0,1],[1,0]] 反diagonal
e₁e₂ --> [[0,1],[-1,0]] 这个是复数i的表示。

接下来有这个公式，它的tensor product第一项实际上用到Cl(2,0), Cl(1,1), Cl(0,2)，这样就可以得到任意Cl(p,q)的structure：



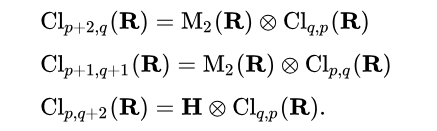
这个公式我还没考虑它的证明，但是它非常好用。

Cl(3,0) = Cl(2,0)⊗Cl(0,1)=M₂(R)⊗C=M₂(C)
Cl(2,1) = Cl(2,0)⊗Cl(1,0)=M₂(R)⊗R²=M₂(R)²=M₂(R²)
Cl(1,2) = Cl(1,1)⊗Cl(0,1)=M₂(R)⊗C=M₂(C)
Cl(1,2) = Cl(0,2)⊗Cl(0,1)=H⊗C
--这个得出两个结果来，它们能isomorphic吗？
Cl(0,3) = Cl(0,2)⊗Cl(1,0)=H⊗R²=H²

然后是4维的。

Cl(4,0)=M₂(H)
Cl(3,1)=M₂(R)⊗M₂(R)=M₂(M₂(R))=M₄(R)
Cl(2,2)=...=M₄(R)
Cl(1,3)=Cl(1,1)⊗Cl(0,2)=M₂(R)⊗H=M₂(H)
Cl(0,4)=...=M₂(H)

这样看Cl(3,1) != Cl(1,3)。但是注意现在都是实数Clifford algebra，也就是over the real，也就是生成元的系数都是实数。

complexisify之后，它们就相等了！也就是允许复数作为系数的话，它们就相等了。这个我还没想明白：

Cl(3,1)⊗C = Cl(1,3)⊗C

这个是Dirac γ matrix用到的Clifford algebra。所以在物理里，Cl(3,1)和Cl(1,3)是一样的。

[pathdream]

这个宇宙只有一个电子

[TheMatrix]

这个宇宙只有一个电子

你是想到了全同粒子？

[pathdream]

你是想到了全同粒子？

我是四维来的 我告诉你这个事实

[TheMatrix]

我是四维来的 我告诉你这个事实

全同粒子不能认为是同一个粒子。我只想提醒你这一点。

[pathdream]

全同粒子不能认为是同一个粒子。我只想提醒你这一点。

这个宇宙只有一个电子

[TheMatrix]

Dirac 4个γ matrix是：

γ⁰= diag(1,1,-1,-1)

γⁱ=[[0,σⁱ],[-σⁱ,0]]

其中σ是Pauli matrix，2X2：

σ¹=[[0,1],[1,0]]
σ²=[[0,-i],[i,0]]
σ³=[[1,0],[0,-1]]

三个Pauli matrix相当于是Cl(3,0)的三个生成元，e₁,e₂,e₃，也就是signature为(+,+,+)的vector space生成的Clifford algebra。因为σ¹σ¹=σ²σ²=σ²σ²=I，并且anticommute。它们不是quarternion的ijk。

Cl(3,0)=Cl(2,0)⊗Cl(0,1)=M₂(R)⊗C=M₂(C)。也就是2X2 Complex matrix。而2X2 Complex matrix作用在C²上。也就是电子的spinor。这好像是对得上。Pauli matrices也是su(2)的生成元。这好像也是对得上的。

Cl(3,1)=Cl(2,0)⊗Cl(1,1)=M₂(R)⊗M₂(R)=M₂(M₂(R))=M₄(R)
complexify it，
Cl(3,1)⊗C=M₄(R)⊗C=M₄(C)
也就是4X4 complex matrix。

这是从signature (+,+,+,-)来的。也就是Minkowski (x,y,z,t) 四维时空。

另一方面，signature改为 (+,-,-,-)的话，也就是把t改为正，xyz改为负的话，

Cl(1,3)=Cl(0,2)⊗Cl(1,1)=H⊗M₂(R)=M₂(H)，2X2 quarternion valued matrix。
complexisfy it，
Cl(1,3)⊗C=M₂(H)⊗C。
这个看不出来等于什么，但是suppose也应该等于M₄(C)。也就是Cl(3,1)和Cl(1,3) complexify之后应该是一样的。

[TheMatrix]

三个Pauli matrix相当于是Cl(3,0)的三个生成元，e₁,e₂,e₃，也就是signature为(+,+,+)的vector space生成的Clifford algebra。因为σ¹σ¹=σ²σ²=σ²σ²=I，并且anticommute。它们不是quarternion的ijk。

哦。quarternion是Cl(3,0)的even grade subalgebra，也就是{1, e₁e₂, e₂e₃, e₃e₁}组成的algebra。

[wdong]

狄拉克方程相当于对薛定谔方程开了平方。数字开平方能开出来正负两个值。方程开平方，也会出来相当于正负两个解，这个正负就是自旋。

[TheMatrix]

狄拉克方程相当于对薛定谔方程开了平方。数字开平方能开出来正负两个值。方程开平方，也会出来相当于正负两个解，这个正负就是自旋。

当年我学C语言，有人告诉我一个类型定义的诀窍，就是一个普通的变量声明前面加上一个typedef，就变成了类型定义。

比如：

int *x;

变成

typedef int *x; //x becomes a type

百试不爽。这就是口诀的威力。你这个贴使我想起了这个口诀。

[liufanghe]

我有一本电子书，现在找不着了。里面讲了Dirac方程的数学来历，和消除平方有关，我觉得讲得挺好的。

是一个数学物理方面的人写的，好像也是个巴西或者阿根廷的作者。

当然，我知道这方面的书很多。我如果找不到那本的话，就随便找一本看看。

找到了望告知一声，记得我老板给我说过一遍
当时就没听明白，一直想了解一下的

[verdelite]

狄拉克方程相当于对薛定谔方程开了平方。数字开平方能开出来正负两个值。方程开平方，也会出来相当于正负两个解，这个正负就是自旋。

不是薛定谔方程开平方，而是Klein-Gordon方程开平方。

[water77]

你们还在玩这么初等的量子力学？
弃婴都不屑回，跟你们玩

[TheMatrix]

找到了望告知一声，记得我老板给我说过一遍
当时就没听明白，一直想了解一下的

没问题。