看图,很形象:https://en.wikipedia.org/wiki/Cusp_(singularity)FoxMe 写了: 2024年 9月 14日 16:57 这个cusp form的定义非常麻烦。一般定义为傅立叶级数的首项为0的modular form,和无穷远点等于0应该是等同的。
但是为啥叫cusp(尖尖)?
Galois group representation
-
forecasting
- 著名点评

- 帖子互动: 365
- 帖子: 4453
- 注册时间: 2023年 4月 17日 08:26
#61 Re: Galois group representation
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#62 Re: Galois group representation
对。是这个函数的问题。
z ---> e2π i z在无穷远点是essential singularity,z以不同的方式趋近于∞时,e2π i z可以取任意值。所以这个函数在无穷远点不连续。所以无穷远点虽然在黎曼球中与实数轴联通,但是被这个函数映射之后可以变成不联通。
我的目的是想说明,经过domain transformation,modular form在0点解析,反过来可以看成modular form在无穷远点解析,或在所有cusp点解析。另外也得出了Fourier变换的形式。
我先写一下看看卡在哪。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#63 Re: Galois group representation
q: z ---> e2π i z这个叫q变换。它把H变成open unit disk D,但是不包括0,因为本来应该是无穷远点变为0,但是e2π i z这个函数在无穷远点是essential singularity,这个地方有点问题,所以先不包括0。不包括0的unit disk叫punctured unit disk,所以这个q变换把H变成了punctured open unit disk,叫D0吧。TheMatrix 写了: 2024年 9月 14日 16:39 modular form和cusp form还可以做domain transformation来看。
z ---> e2π i z 这个函数把 H 变为单位圆内,又叫unit disk,D。如果z为实数的话,e2π i z在单位圆上。但是H不包括实数轴,所以H会变到单位圆内,不包括圆周。而且这不是一一映射,e2π i z是周期函数,所以这个变换是很多层的cover。从实数轴的变换看,它是一圈一圈的在单位圆周上绕。
所以实数轴上的cusp,在这个变换下,会变成单位圆周上的点。
而无穷远点∞,在这个变换下,应该是变成圆心。因为如果z=x+iy,取x=0,y --> ∞ 的话,e2π i z越来越小,趋近于0。
但是从黎曼球或者CP1来看,无穷远点和实数轴应该是联通的,但是这里分别变换成圆心和圆周,是不联通的。这是为什么呢?
这个q变换是个周期函数,一圈一圈的绕嘛。另一方面,一个modular form f: z --> C也是周期函数,和q变换的周期一样,都是1。所以f通过q变换可以定义一个D0上的函数:g: D0 --> C,也是解析函数。它的定义是:g(q)=f(z) if q = e2π i z。
目前是没问题的。
然后我要说,g函数在0点也解析。所以就有解析函数的展开,也就是泰勒展开:
g(q)=a0+a1q+a2q2+...
同时也有了f(z)的傅里叶展开:
f(z)=g(q)=a0+a1e2π i z+a2e2π i 2z+...
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#64 Re: Galois group representation
或者可以反过来说,从modular form f这边看,它是一个周期函数,因此有傅里叶展开:TheMatrix 写了: 2024年 9月 15日 08:57 q: z ---> e2π i z这个叫q变换。它把H变成open unit disk D,但是不包括0,因为本来应该是无穷远点变为0,但是e2π i z这个函数在无穷远点是essential singularity,这个地方有点问题,所以先不包括0。不包括0的unit disk叫punctured unit disk,所以这个q变换把H变成了punctured open unit disk,叫D0吧。
这个q变换是个周期函数,一圈一圈的绕嘛。另一方面,一个modular form f: z --> C也是周期函数,和q变换的周期一样,都是1。所以f通过q变换可以定义一个D0上的函数:g: D0 --> C,也是解析函数。它的定义是:g(q)=f(z) if q = e2π i z。
目前是没问题的。
然后我要说,g函数在0点也解析。所以就有解析函数的展开,也就是泰勒展开:
g(q)=a0+a1q+a2q2+...
同时也有了f(z)的傅里叶展开:
f(z)=g(q)=a0+a1e2π i z+a2e2π i 2z+...
f(z)=a0+a1e2π i z+a2e2π i 2z+...
而做q变换之后,q: z ---> e2π i z,有:
g(q)=a0+a1q+a2q2+...
也就是说g(q)在punctured unit disk上解析,除了0点不知道,0点的邻域都解析。
这个地方要用到modular form的growth condition,做q变换之后它意味着g(q)在零点附近是bounded。因此g(q)在零点不能是essential singularity,也不能是pole,只能是解析。
不满足growth condition但是modular的函数确实存在,ChatGPT给了pole和essential singularity的例子:
modular form with pole at ∞:

modular form with essential singularity at ∞:

-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#65 Re: Galois group representation
所以这个q-变换挺好。q-变换把modular form变成了圆内的解析函数,解析性包括0点。但是还不能完全地说q-变换把无穷远点变成0点。0点的解析性是通过growth condition补全的。TheMatrix 写了: 2024年 9月 15日 10:05 或者可以反过来说,从modular form f这边看,它是一个周期函数,因此有傅里叶展开:
f(z)=a0+a1e2π i z+a2e2π i 2z+...
而做q变换之后,q: z ---> e2π i z,有:
g(q)=a0+a1q+a2q2+...
也就是说g(q)在punctured unit disk上解析,除了0点不知道,0点的邻域都解析。
这个地方要用到modular form的growth condition,做q变换之后它意味着g(q)在零点附近是bounded。因此g(q)在零点不能是essential singularity,也不能是pole,只能是解析。
实数轴上的cusp,也就是有理数点,q-变换之后变成了圆周上的有理数点。无穷远点这个cusp,还是不能说它变到了0点。这个地方还是有一点点问题。almost。我看到很多地方说 i∞,可以理解为无穷远点的“一部分”,或者某种方式的无穷远点。不完全严格。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#66 Re: Galois group representation
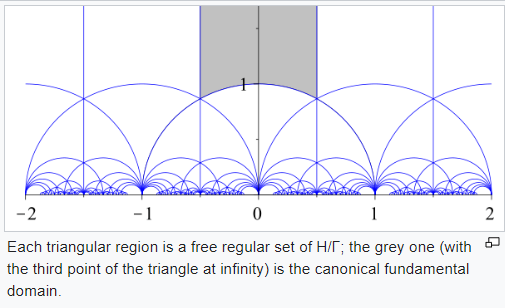
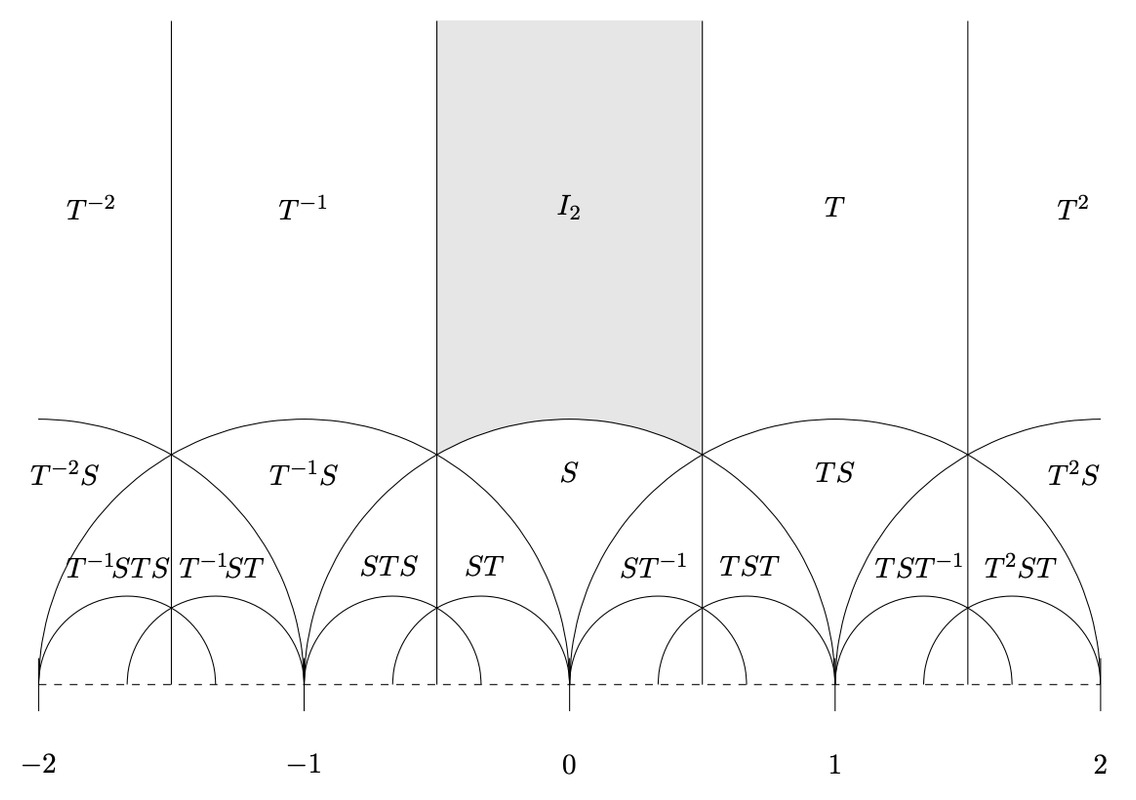
如果考虑H在SL(2,Z)作用下的fundamental domain的话,只有竖长条那个fundamental domain包含无穷远点。而这个fundamental domain中的无穷远点在q-变换下只能变到0点,因为这个domain限制了趋近于无穷远点的方式。TheMatrix 写了: 2024年 9月 15日 10:28 所以这个q-变换挺好。q-变换把modular form变成了圆内的解析函数,解析性包括0点。但是还不能完全地说q-变换把无穷远点变成0点。0点的解析性是通过growth condition补全的。
实数轴上的cusp,也就是有理数点,q-变换之后变成了圆周上的有理数点。无穷远点这个cusp,还是不能说它变到了0点。这个地方还是有一点点问题。almost。我看到很多地方说 i∞,可以理解为无穷远点的“一部分”,或者某种方式的无穷远点。不完全严格。
这个也挺有意思:fundamental domain“分割”了无穷远点,无穷远点一点也没少,但是q-变换下每个fundamental domain中的无穷远点都只能变换到0。其他的值没有了。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#67 Re: Galois group representation
看了几个版本的Hecke operator的定义:
Wolfram的:
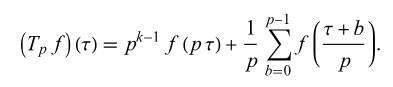
Wikipedia的:
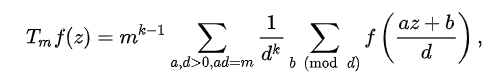
ChatGPT的:
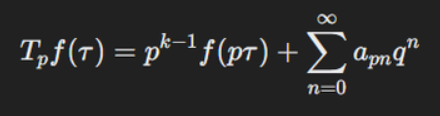
我觉得还是Wolfram的最好理解。这里是p为素数的情况。
Wiki的没有给p为素数的简化形式,公式看起来比较繁琐。
ChatGPT的把函数和它的傅里叶展开混在一起用,好像理解起来需要转换思维。
Wolfram的:
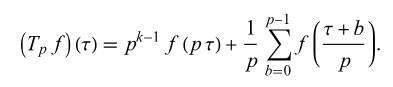
Wikipedia的:
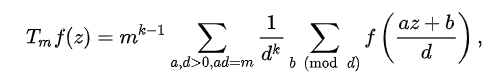
ChatGPT的:
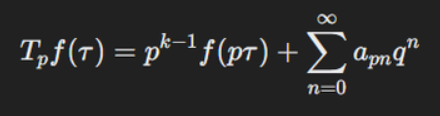
我觉得还是Wolfram的最好理解。这里是p为素数的情况。
Wiki的没有给p为素数的简化形式,公式看起来比较繁琐。
ChatGPT的把函数和它的傅里叶展开混在一起用,好像理解起来需要转换思维。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#68 Re: Galois group representation
基本特征是变量的缩放,τ --> pτ,和 τ --> τ/p。TheMatrix 写了: 2024年 9月 15日 14:06 看了几个版本的Hecke operator的定义:
Wolfram的:
Wikipedia的:
ChatGPT的:
我觉得还是Wolfram的最好理解。这里是p为素数的情况。
Wiki的没有给p为素数的简化形式,公式看起来比较繁琐。
ChatGPT的把函数和它的傅里叶展开混在一起用,好像理解起来需要转换思维。
因为modular form是周期函数,周期为1,变量的缩放导致周期的缩放。
f(pτ)的周期是1/p,对应着傅里叶展开项中 e2π i n/p τ 以及系数 an/p。
f(τ/p)的周期是p,对应着傅里叶展开项中 e2π i p*n τ 以及系数 ap*n。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#69 Re: Galois group representation
第一项对应:TheMatrix 写了: 2024年 9月 15日 14:25 基本特征是变量的缩放,τ --> pτ,和 τ --> τ/p。
因为modular form是周期函数,周期为1,变量的缩放导致周期的缩放。
f(pτ)的周期是1/p,对应着傅里叶展开项中 e2π i n/p τ 以及系数 an/p。
f(τ/p)的周期是p,对应着傅里叶展开项中 e2π i p*n τ 以及系数 ap*n。
a0+a1qp+a2q2p+a3q3p+...
第二项对应:
a0+apq+a2pq2+a3pq3+...
其他的an项被互相cancel掉了。
所以可以写成
Σn pk-1anqnp+anpqn
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#70 Re: Galois group representation
变量的缩放对应傅里叶系数的拉伸。所以这是一个对傅里叶系数的操作。TheMatrix 写了: 2024年 9月 16日 16:27 第一项对应:
a0+a1qp+a2q2p+a3q3p+...
第二项对应:
a0+apq+a2pq2+a3pq3+...
其他的an项被互相cancel掉了。
所以可以写成
Σn pk-1anqnp+anpqn
但是关键是这样变换之后仍然是weight-k modular form。这样它才成为一个operator。
第一项和第二项本身,都不再是SL(2,Z)的modular form,需要相加才回到SL(2,Z)的modular form。
第一项本身是Γ0(p)的modular form,这是SL(2,Z)的一个子群。
第二项本身是Γ(p)的modular form,这是SL(2,Z)的一个更小的子群。
但是两项相加,又回到了SL(2,Z)的modular form。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#71 Re: Galois group representation
也就是如何调整傅里叶系数,使结果仍然是modular form。TheMatrix 写了: 2024年 9月 16日 17:13 变量的缩放对应傅里叶系数的拉伸。所以这是一个对傅里叶系数的操作。
但是关键是这样变换之后仍然是weight-k modular form。这样它才成为一个operator。
第一项和第二项本身,都不再是SL(2,Z)的modular form,需要相加才回到SL(2,Z)的modular form。
第一项本身是Γ0(p)的modular form,这是SL(2,Z)的一个子群。
第二项本身是Γ(p)的modular form,这是SL(2,Z)的一个更小的子群。
但是两项相加,又回到了SL(2,Z)的modular form。
傅里叶系数就是一个数列,列出来,调整一下间距,挺直观的。但是不能乱动。动完了还得是modular form才行。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#72 Re: Galois group representation
或者说modular form的傅里叶系数应该有什么规律?TheMatrix 写了: 2024年 9月 16日 19:23 也就是如何调整傅里叶系数,使结果仍然是modular form。
傅里叶系数就是一个数列,列出来,调整一下间距,挺直观的。但是不能乱动。动完了还得是modular form才行。
这类问题是傅里叶变换的永恒pattern。永远有。因为永远也解决不完。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#73 Re: Galois group representation
比如一个modular form f的傅里叶系数是 (a0,a1,a2,a3,...),TheMatrix 写了: 2024年 9月 16日 19:23 也就是如何调整傅里叶系数,使结果仍然是modular form。
傅里叶系数就是一个数列,列出来,调整一下间距,挺直观的。但是不能乱动。动完了还得是modular form才行。
取 p=7,
第一步,dilation,拉伸7倍:
(a0,0,0,0,0,0,0,a1,0,0,0,0,0,0,a2,0,0,0,0,0,0,a3,...)
第二步,shrink,每隔7个取一个:
(a0,a7,a14,a21,....)
这样得到两个数列。
第三步,数列1乘以7k-1 + 数列2,得到一个新数列。这个数列还是一个modular form(的傅里叶系数)!
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#74 Re: Galois group representation
就是玩数列。TheMatrix 写了: 2024年 9月 16日 21:30 比如一个modular form f的傅里叶系数是 (a0,a1,a2,a3,...),
取 p=7,
第一步,dilation,拉伸7倍:
(a0,0,0,0,0,0,0,a1,0,0,0,0,0,0,a2,0,0,0,0,0,0,a3,...)
第二步,shrink,每隔7个取一个:
(a0,a7,a14,a21,....)
这样得到两个数列。
第三步,数列1乘以7k-1 + 数列2,得到一个新数列。这个数列还是一个modular form(的傅里叶系数)!
但不是乱来的。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#76 Re: Galois group representation
SL(2,Z)是由两个元素生成的,T 和 S,T是translation by 1:z --> z+1,S是negative reciprocal:z --> -1/z。TheMatrix 写了: 2024年 9月 17日 17:07 Henri Cohen的书好像是一本经典教材。下面是他的一个简写本:
https://arxiv.org/pdf/1809.10907
T=[1 1; 0 1], S=[0 -1; 1 0]。
证明一个函数具有modular性质,叫modularity,只需证明它在T和S下具有modularity就行了。这个我还没看出来为什么这样就够了。
在T下具有modularity就是:f(Tz)=f(z),或者f(z+1)=f(z),也就是周期性。
在S下具有modularity就是:f(Sz)=f(-1/z)=zkf(z)。
这就是证明了f具有modularity。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#77 Re: Galois group representation
这个可以用类似数学归纳法来证明。TheMatrix 写了: 2024年 9月 17日 17:16 SL(2,Z)是由两个元素生成的,T 和 S,T是translation by 1:z --> z+1,S是negative reciprocal:z --> -1/z。
T=[1 1; 0 1], S=[0 -1; 1 0]。
证明一个函数具有modular性质,叫modularity,只需证明它在T和S下具有modularity就行了。这个我还没看出来为什么这样就够了。
在T下具有modularity就是:f(Tz)=f(z),或者f(z+1)=f(z),也就是周期性。
在S下具有modularity就是:f(Sz)=f(-1/z)=zkf(z)。
这就是证明了f具有modularity。
任何一个SL(2,Z)都可以写成T和S的组合,包括它们的逆。SS=1,所以S的逆就是S。T的逆就是 z --> z-1。
所以只需证明对于任意 A = [a b; c d] ∈ SL(2,Z),如果 f 在A的作用下有modularity,也就是 f(Az)=(cz+d)k f(z),那么 f在TA,T-1A,SA,作用下仍然有modularity,就行了。把T和S矩阵代入验证就可以了。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#78 Re: Galois group representation
接下来是证明一个modular form f,在Hecke operator作用下仍有modularity。TheMatrix 写了: 2024年 9月 18日 15:32 这个可以用类似数学归纳法来证明。
任何一个SL(2,Z)都可以写成T和S的组合,包括它们的逆。SS=1,所以S的逆就是S。T的逆就是 z --> z-1。
所以只需证明对于任意 A = [a b; c d] ∈ SL(2,Z),如果 f 在A的作用下有modularity,也就是 f(Az)=(cz+d)k f(z),那么 f在TA,T-1A,SA,作用下仍然有modularity,就行了。把T和S矩阵代入验证就可以了。
对于p为素数,Hecke operator定义为:
(Tpf)(z) = pk-1f(pz) + 1/p ( f(z/p) + f((z+1)/p + ... + f((z+p-1)/p) )
这个要借助于T和S。有了这两个也不容易。说明这个操作的拼凑是很精妙的。
也就是要证明
(Tpf)(Tz) = (Tpf)(z)
和
(Tpf)(Sz) = zk (Tpf)(z)
第一个利用到 {f(z/p), f((z+1)/p, ..., f((z+p-1)/p)} 在T的作用下的循环对称性。
第二个利用到 {f(z/p), f((z+1)/p, ..., f((z+p-1)/p)} 在S作用下的乘法群的对称性。
所以这些项的拼凑,以及系数的拼凑,都是相当精妙的。这也代表了在傅里叶系数上的操作与拼凑。
据说源于Ramanujan的 Δ-form。
我感觉有点类似于Dirichlet character的发现。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#79 Re: Galois group representation
TheMatrix 写了: 2024年 9月 18日 15:49 接下来是证明一个modular form f,在Hecke operator作用下仍有modularity。
对于p为素数,Hecke operator定义为:
(Tpf)(z) = pk-1f(pz) + 1/p ( f(z/p) + f((z+1)/p + ... + f((z+p-1)/p) )
这个要借助于T和S。有了这两个也不容易。说明这个操作的拼凑是很精妙的。
也就是要证明
(Tpf)(Tz) = (Tpf)(z)
和
(Tpf)(Sz) = zk (Tpf)(z)
第一个利用到 {f(z/p), f((z+1)/p, ..., f((z+p-1)/p)} 在T的作用下的循环对称性。
第二个利用到 {f(z/p), f((z+1)/p, ..., f((z+p-1)/p)} 在S作用下的乘法群的对称性。
所以这些项的拼凑,以及系数的拼凑,都是相当精妙的。这也代表了在傅里叶系数上的操作与拼凑。
据说源于Ramanujan的 Δ-form。
我感觉有点类似于Dirichlet character的发现。

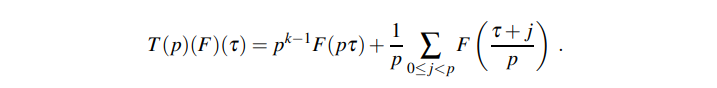

最后这段,他说很简单。其实不简单。我觉得里面还是很精妙的。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 286
- 帖子: 13824
- 注册时间: 2022年 7月 26日 00:35
#80 Re: Galois group representation
可以这样看:
假设有一个modular form f,我们要对它做一些操作,这个操作必须是容易在傅里叶系数上实现的。
start with f(pz)。这个傅里叶系数上很容易操作的。
但是它不modular。它不modular with respect to the full modular group SL(2,Z)。它modular with respect to a subgroup of the modular group。那也不行,我们要求它必须modular with respect to the full modular group SL(2,Z)。
也就是看它到底哪里不modular。
用T和S来作用它。
T作用它,等于 f(pTz)=f(p(z+1))=f(pz+p)=f(pz)。所以在T下modular。虽然它的周期拉长了。
S作用它,等于 f(pSz)=f(-p/z)=f(S.(z/p))=(z/p)kf(z/p)。
出来了一个新的东西 f(z/p)。把它包含进去,希望能闭环。
有它就要有 f(Tz/p),也就是f((z+1)/p)。这又是一个新的东西。
再做T,f(TTz/p),就是 f((z+2)/p)。。。一直做到 f((z+p-1)/p),再做就循环了。
所以这就是全部。。。对T是全部。
然后还要对S闭环。。。这里正好是已经对S闭环了。也许可以对S不闭环,那就需要对S进行扩展。
也就是对S和T交替扩展直至闭环。
然后还要拼凑系数。
这样就得到一个新的modular form。。。的产生方式。