i和1正交吗?
版主: verdelite, TheMatrix
Re: i和1正交吗?
你这是混淆了数域和向量空间。 当你做了同构变换 i-e_y, 1-e_x以后,在实数域上的由正交基(e_x,e_y)张成的向量空间里,e_x和e_y正交。
在复数域上,就不能做这样的同构变换,i和1都只能映射为一维向量,它们平行。
在复数域上,就不能做这样的同构变换,i和1都只能映射为一维向量,它们平行。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
Re: i和1正交吗?
应该是把每一维的复数轴扩展成二维的实数轴。
(i,i)--->(0,1,0,1)
(1,2)--->(1,0,2,0)
这样在这个扩展的四维实空间就正交了。
曾经的 newkids_on_the_block
Re: i和1正交吗?
我觉得这个矛盾是Hermitian inner product的一个缺陷。如果把内积定义为Hermitian inner product的实部:
Re{<x,y>}
就能消除这个矛盾。但是,这个内积定义又会导致其它的问题。
Re{<x,y>}
就能消除这个矛盾。但是,这个内积定义又会导致其它的问题。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
Re: i和1正交吗?
Hermitian inner product的定义是很特殊。首先它是一个bilinear form。FoxMe 写了: 2023年 3月 29日 16:01 我觉得这个矛盾是Hermitian inner product的一个缺陷。如果把内积定义为Hermitian inner product的实部:
Re{<x,y>}
就能消除这个矛盾。但是,这个内积定义又会导致其它的问题。
但是它不是symmetric的,也不是anti-symmetric的,而是sesquilinear form。这里糅合了一个conjugation,也是一个involution。把这些糅合在一起,也是很精妙的,不能说是缺陷,我觉得。
Re: i和1正交吗?
这和“1和i在实数域上线性无关、但在复数域上线性相关”是同一个性质吧。
正交的概念也好,线性相关的概念也好,都取决于定义。涉及到线性空间的话,也取决于是哪一个数域上的。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
Re: i和1正交吗?
哦不对。sesquilinear不是bilinear的。第一项是linear的,第二项是conjugate linear的。TheMatrix 写了: 2023年 3月 29日 16:09 Hermitian inner product的定义是很特殊。首先它是一个bilinear form。
但是它不是symmetric的,也不是anti-symmetric的,而是sesquilinear form。这里糅合了一个conjugation,也是一个involution。把这些糅合在一起,也是很精妙的,不能说是缺陷,我觉得。
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
Re: i和1正交吗?
我在想quadratic form的时候,好像有一个问题和你这里的类似。FoxMe 写了: 2023年 3月 29日 11:20 复数i和1正交吗?
二者的夹角是90度,显然正交。
但是在复空间做Hermitian inner product, <i,1>=i,不为0,所以它们不正交。
这个问题我问过好几个人,没有得到满意的答案。
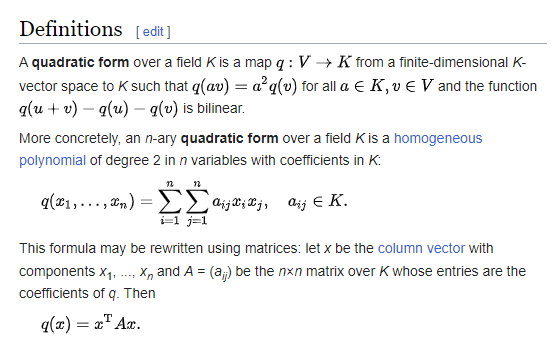
quadratic form,我除了正定的情况,其他的没怎么细想过。今天想Real Clifford algebra的时候,突然出现一个困惑。
就是一个二维Real vector space,假设上面有一个quadratic form Q,nondegenerate,signature 为 (1,-1)。也就是有一个basis (e1, e2),Q(e1)=1,Q(e2)=-1。
那么Q(e1+e2)应该等于多少?
我开始把它想成复数空间了,e1对应1,e2对应i,Q想象成了z2,但是这就不是Real quadratic space了。
后来发现Q(e1+e2)应该等于0。你觉得这个对不对?
那么对于一个非正定nondegenerate的quadratic form Q,可以有v !=0 but Q(v)=0。
Re: i和1正交吗?
展开Q(e_1+e_2, e_1+e_2)就可以算了。TheMatrix 写了: 2023年 3月 30日 21:31 我在想quadratic form的时候,好像有一个问题和你这里的类似。
quadratic form,我除了正定的情况,其他的没怎么细想过。今天想Real Clifford algebra的时候,突然出现一个困惑。
就是一个二维Real vector space,假设上面有一个quadratic form Q,nondegenerate,signature 为 (1,-1)。也就是有一个basis (e1, e2),Q(e1)=1,Q(e2)=-1。
那么Q(e1+e2)应该等于多少?
我开始把它想成复数空间了,e1对应1,e2对应i,Q想象成了z2,但是这就不是Real quadratic space了。
后来发现Q(e1+e2)应该等于0。你觉得这个对不对?
那么对于一个非正定nondegenerate的quadratic form Q,可以有v !=0 but Q(v)=0。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
Re: i和1正交吗?
Quadratic form Q两个变量。说一个变量,一般是指两个变量相等的情况:Q(e) = Q(e, e)。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
Re: i和1正交吗?
This is all fine.
However, in my mind, I like to start with Q(x, y) = x^TAy, where A is symmetric matrix. Then, a quadratic form is Q(x) = Q(x, x). Thus, Q(x+y) = Q(x+y, x+y) = Q(x, x) + Q(x, y) + Q(y, x) + Q(y, y).
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
Re: i和1正交吗?
哦,你要是这么说的话,也是严格的。YWY 写了: 2023年 3月 31日 11:26 This is all fine.
However, in my mind, I like to start with Q(x, y) = x^TAy, where A is symmetric matrix. Then, a quadratic form is Q(x) = Q(x, x). Thus, Q(x+y) = Q(x+y, x+y) = Q(x, x) + Q(x, y) + Q(y, x) + Q(y, y).