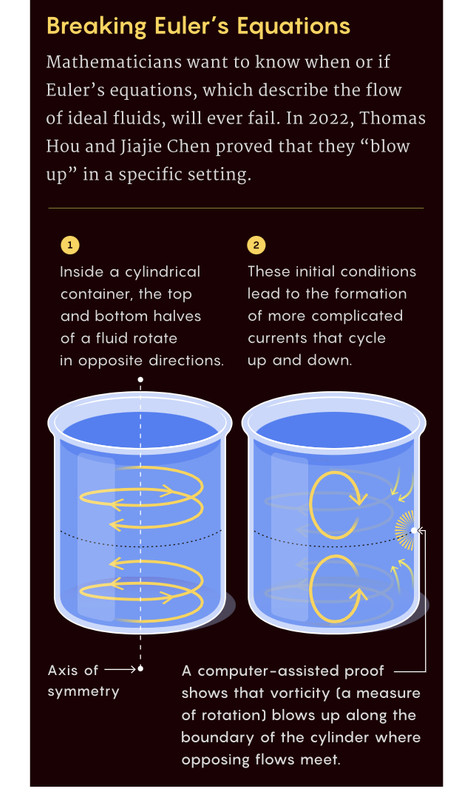
https://www.quantamagazine.org/computer ... -20221116/
Perhaps the oldest and most prominent of these equations, formulated by Leonhard Euler more than 250 years ago, describe the flow of an ideal, incompressible fluid: a fluid with no viscosity, or internal friction, that cannot be forced into a smaller volume. “Almost all nonlinear fluid equations are kind of derived from the Euler equations,” said Tarek Elgindi, a mathematician at Duke University. “They’re the first ones, you could say.”
https://arxiv.org/abs/2210.07191
In a preprint posted online last month, a pair of mathematicians has shown that a particular version of the Euler equations does indeed sometimes fail. The proof marks a major breakthrough — and while it doesn’t completely solve the problem for the more general version of the equations, it offers hope that such a solution is finally within reach. “It’s an amazing result,” said Tristan Buckmaster, a mathematician at the University of Maryland who was not involved in the work. “There are no results of its kind in the literature.”
The 177-page proof — the result of a decade-long research program — makes significant use of computers. This arguably makes it difficult for other mathematicians to verify it. (In fact, they are still in the process of doing so, though many experts believe the new work will turn out to be correct.) It also forces them to reckon with philosophical questions about what a “proof” is, and what it will mean if the only viable way to solve such important questions going forward is with the help of computers.
To get the tight bounds they needed on all these different terms, Hou and Chen broke the inequality into two major parts. They could take care of the first part by hand, with techniques including one that dates back to the 18th century, when the French mathematician Gaspard Monge sought an optimal way of transporting soil to build fortifications for Napoleon’s army. “Stuff like this has been done before, but I found it striking that [Hou and Chen] used it for this,” Fefferman said.
That left the second part of the inequality. Tackling it would require computer assistance. For starters, there were so many calculations that needed to be done, and so much precision required, that “the amount of work you’d have to do with pencil and paper would be staggering,” de la Llave said. To get various terms to balance out, the mathematicians had to perform a series of optimization problems that are relatively easy for computers but exceedingly time-consuming for humans. Some of the values also depended on quantities from the approximate solution; since that was calculated using a computer, it was more straightforward to also use a computer to perform these additional computations.





