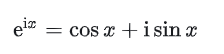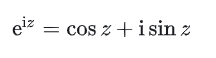STEM版,合并数学,物理,化学,科学,工程,机械。不包括生物、医学相关,和计算机相关内容。
版主: verdelite , TheMatrix
TheMatrix 楼主
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 260 帖子: 13169 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 楼主 2024年 12月 30日 17:20
上次由 TheMatrix 在 2024年 12月 30日 17:22 修改。
原因: 未提供修改原因
dealfinder10
论坛精英
帖子互动: 726 帖子: 6422 注册时间: 2023年 10月 6日 14:56
帖子
由 dealfinder10 2024年 12月 30日 17:30
没学过高数和复变?taylor展开啊。
TheMatrix 楼主
论坛支柱2024年度优秀版主 TheMatrix 的博客
帖子互动: 260 帖子: 13169 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix 楼主 2024年 12月 30日 17:42
princeton (wow)
知名人士
帖子互动: 3 帖子: 55 注册时间: 2022年 10月 15日 17:20
帖子
由 princeton (wow) 2024年 12月 31日 12:49
是自定义的!Taylor展开需要对这个复指数函数求导,但复指数函数在欧拉公式前还没有定义呢!
Pegasi
知名作家
帖子互动: 69 帖子: 1213 注册时间: 2022年 10月 22日 12:50
帖子
由 Pegasi 2024年 12月 31日 12:51
princeton 写了: 2024年 12月 31日 12:49
是自定义的!Taylor展开需要对这个复指数函数求导,但复指数函数在欧拉公式前还没有定义呢!
用的实函数求导的形式
Pegasi
知名作家
帖子互动: 69 帖子: 1213 注册时间: 2022年 10月 22日 12:50
帖子
由 Pegasi 2024年 12月 31日 12:53
红帝上昨天刚看的
princeton (wow)
知名人士
帖子互动: 3 帖子: 55 注册时间: 2022年 10月 15日 17:20
帖子
由 princeton (wow) 2024年 12月 31日 12:59
Pegasi 写了: 2024年 12月 31日 12:51
用的实函数求导的形式
复指数函数还没定义呀,除非用Taylor展开来定义,这部就是欧拉公式么:-)
mmking (上水)
论坛支柱
帖子互动: 1187 帖子: 8608 注册时间: 2023年 1月 25日 05:10
帖子
由 mmking (上水) 2024年 12月 31日 20:12
凡所有相,皆是虚妄
FoxMe (令狐)
著名点评
帖子互动: 132 帖子: 5174 注册时间: 2022年 7月 26日 16:46
帖子
由 FoxMe (令狐) 2025年 1月 2日 12:36
欧拉是通过级数展开来证明的。但是中学是怎么教的?我记得是定义的:eix = cosx + i sinx,没有证明,只要求背公式(但是我也可能记错了)
(ヅ)
论坛支柱
帖子互动: 544 帖子: 11677 注册时间: 2022年 8月 21日 14:20
帖子
由 (ヅ) 2025年 1月 6日 19:26
有一个证明就是用泰勒展开sinx和cosx然后凑出来e^{ix}的泰勒展开形式