GPT4o这个答案不符合要求。她说要“recompute the hash scores for each object to redistribute them among the shards.”,这是不可接受的。
"“recompute the hash scores for each object to redistribute them among the shards.“ is not acceptable. We want to minimize redistribution. Ideally, no redistribution."
这是新答案:
Ah, I see! Thank you for clarifying that **minimizing redistribution** (ideally **no redistribution**) is a critical requirement. This makes the problem more challenging but also aligns well with the fundamental benefit of **Rendezvous Hashing**, which is to minimize changes when shards are added or removed.
Let’s refine the solution to satisfy these constraints:
---
### Key Objective
We must:
1. **Add new shards dynamically** while ensuring that the distribution of objects remains balanced.
2. **Minimize or avoid redistribution** of objects already assigned to existing shards.
---
### Revisiting Rendezvous Hashing with Weighted Shards
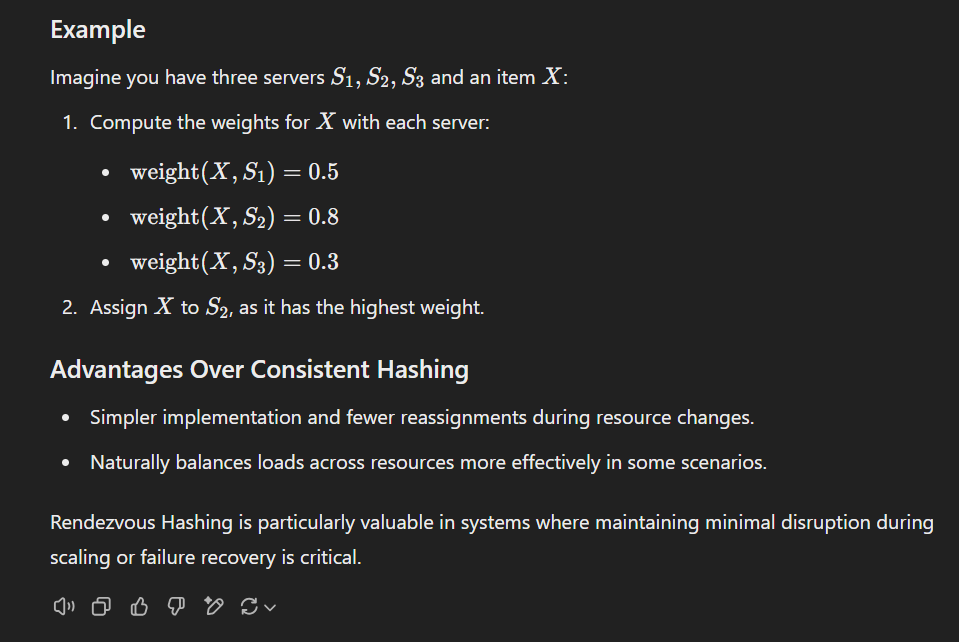
In Rendezvous Hashing (also called Highest Random Weight hashing), each object is mapped to a shard by computing a weighted score for each shard. The shard with the **highest score** is chosen for the object.
For shard \( S_i \), the score for an object \( O \) is computed as:
\[
\text{score}(S_i, O) = h(S_i, O) \times w_i,
\]
where:
- \( h(S_i, O) \) is the hash of the shard \( S_i \) and object \( O \), normalized to a value between 0 and 1.
- \( w_i \) is the weight of shard \( S_i \).
Objects are assigned to the shard with the highest score. When a new shard is added, only objects that score higher for the new shard will move to it, which ensures minimal redistribution.
---
### Weight Adjustment for New Shards
We can use a **progressive weight adjustment scheme** that ensures fairness while preventing unnecessary redistribution. Here's how it works:
1. **Initial Weights for Existing Shards**:
Let the current number of shards be \( n \). Assign equal weights to all existing shards initially:
\[
w_i = 1, \quad \text{for } i = 1, 2, \dots, n.
\]
2. **Weight for the New Shard**:
When adding a new shard, assign it a higher weight (e.g., \( w_{\text{new}} > 1 \)), but scale it down progressively as more shards are added. A good choice for the new shard’s weight is:
\[
w_{\text{new}} = \frac{c}{n},
\]
where \( c > 1 \) is a constant that controls the initial bias toward the new shard. This ensures that the new shard is more likely to attract new objects, while existing objects remain largely unaffected.
3. **Dynamic Weight Normalization**:
To avoid large deviations in the distribution, normalize all weights so that the total weight remains proportional to the number of shards:
\[
\hat{w}_i = \frac{w_i}{\sum_{j=1}^{n+1} w_j}.
\]
---
### Why Redistribution Is Minimized
In Rendezvous Hashing, an object \( O \) is **only reassigned** to a new shard if the new shard’s score is higher than its current shard’s score. By carefully assigning weights to the new shard, we ensure that:
1. Most objects will remain with their original shard because the new shard’s weight is not drastically higher than the existing shards.
2. The objects that do move will naturally tend to be objects that are **better suited** for the new shard due to its higher weight.
This property of Rendezvous Hashing inherently minimizes redistribution, as only objects that are more closely associated with the new shard (based on the hash function and weights) will move.
---
### Mathematical Soundness of the Weight Scheme
The key to minimizing redistribution while maintaining fairness is to control the bias introduced by new shards. Using the weight scheme \( w_{\text{new}} = \frac{c}{n} \), we achieve the following:
1. **Initial Bias Toward New Shards**:
When the system is small (i.e., \( n \) is small), the new shard receives a relatively large weight, encouraging new objects to be assigned to it.
2. **Convergence to Uniformity**:
As \( n \) grows, \( w_{\text{new}} \) decreases, ensuring that the distribution of objects across shards becomes more uniform over time.
3. **Bounded Redistribution**:
The redistribution of objects is bounded by the difference in weights between the new shard and the existing shards. This difference decreases as \( n \) increases, leading to minimal disruption as the system grows.
---
### Example Walkthrough
#### Initial State:
Suppose there are 2 shards:
- Shard 1 weight: \( w_1 = 1 \),
- Shard 2 weight: \( w_2 = 1 \).
#### Add a New Shard:
1. Compute the new shard's weight:
\[
w_{\text{new}} = \frac{c}{n} = \frac{2}{2} = 1, \quad \text{(assuming \( c = 2 \))}.
\]
Now all shards have equal weights:
\[
w_1 = w_2 = w_{\text{new}} = 1.
\]
This results in no redistribution because the weights are balanced.
#### Add Another Shard:
1. Compute the new shard's weight:
\[
w_{\text{new}} = \frac{c}{n} = \frac{2}{3}.
\]
Normalize the weights:
\[
w_1 = w_2 = w_3 = 1, \quad w_{\text{new}} = \frac{2}{3}.
\]
Redistribution will only occur for objects that hash to a significantly higher score for the new shard, which ensures minimal disruption.
---
### Final Thoughts
By carefully controlling the weights of new shards, we can ensure that:
- Redistribution is minimized (only objects that strongly favor the new shard will move).
- The system remains balanced, with new shards initially receiving more objects but converging to uniformity over time.
This approach leverages the natural properties of Rendezvous Hashing to handle dynamic scaling gracefully without requiring a complete reassignment of objects. Let me know if you’d like further clarification or refinements!
hci 写了: 2025年 1月 28日 01:04
这个题目是我写码中遇到的的真实问题。
GPT 4o写答案写了一半就终止了,我让它“go on",它才写完,你们看看对不对?
Let’s continue and refine the approach to ensure the distribution of objects remains fair and balanced while dynamically adding new shards with appropriately adjusted weights.
---
### Step 3 (Continued): Weight Assignment Strategy
We want the weight of the new shard to be slightly higher than the existing shards initially, which allows it to attract more objects when first added. However, as more shards are added, the weights of all shards should balance over time.
#### Weight Formulas:
1. **Existing Shards**:
For existing shards, scale their weights based on the current number of shards, \( n \), and ensure their total weight decreases slightly to account for the introduction of the new shard.
\[
w_i = \frac{1}{n^2}, \quad \text{for all existing shards (i = 1, 2, ..., n)}.
\]
2. **New Shard**:
The weight of the new shard is set slightly higher to initially attract more objects. A good formula for the new shard weight is:
\[
w_{new} = \frac{1}{n^2} \cdot (1 + k),
\]
where \( k \) is a small constant that determines the bias toward the new shard. For example, \( k = 1 \) means the new shard gets twice the weight of existing shards initially.
3. **Normalization**:
After assigning weights, normalize them so that the total weight \( W \) sums to 1. This ensures the probabilities are well-defined:
\[
W = \sum_{i=1}^{n} w_i + w_{new}.
\]
Normalize by dividing each weight by \( W \).
---
### Step 4: Dynamic Adjustment Over Time
As more shards are added, the weights of all shards will need to adjust dynamically to maintain fairness. The key is to reduce the bias of the new shard's weight as the total number of shards increases.
The bias factor \( k \) can be made a function of \( n \) (e.g., decrease \( k \) as \( n \) grows). For example:
\[
k = \frac{c}{n},
\]
where \( c \) is a constant. This ensures that the bias \( k \) diminishes as the number of shards increases, leading to a more uniform distribution.
---
### Algorithm for Adding a New Shard
1. **Calculate Base Weight for Existing Shards**:
Assign each existing shard a weight proportional to \( \frac{1}{n^2} \), where \( n \) is the current number of shards.
2. **Assign Weight to the New Shard**:
Use the formula:
\[
w_{new} = \frac{1}{n^2} \cdot (1 + \frac{c}{n}),
\]
where \( c \) is a constant controlling the initial bias.
3. **Normalize Weights**:
After assigning weights, normalize them so that the total weight equals 1:
\[
w_i = \frac{w_i}{W}, \quad W = \sum_{i=1}^{n+1} w_i.
\]
4. **Rehash Objects**:
Using the new weights, recompute the hash scores for each object to redistribute them among the shards.
---
### Step 5: Mathematical Soundness
This approach satisfies the following properties:
1. **Fairness**:
Over time, the weights of all shards converge to uniformity, ensuring a fair distribution of objects.
2. **Bias for New Shards**:
New shards initially attract more objects due to their slightly higher weight, which helps balance the load when they are introduced.
3. **Scalability**:
As the number of shards grows, the bias diminishes, and the system smoothly transitions to an even distribution.
---
### Example Walkthrough
#### Initial State:
Suppose you have 2 shards:
- Shard 1 weight: \( w_1 = 0.5 \),
- Shard 2 weight: \( w_2 = 0.5 \).
#### Adding a New Shard:
1. Set \( n = 2 \) (current number of shards).
2. Assign weights:
- Existing shards: \( w_1 = w_2 = \frac{1}{n^2} = \frac{1}{4} = 0.25 \),
- New shard: \( w_{new} = \frac{1}{4} \cdot (1 + \frac{1}{2}) = 0.375 \).
3. Normalize:
Total weight \( W = 0.25 + 0.25 + 0.375 = 0.875 \).
Normalized weights:
- \( w_1 = \frac{0.25}{0.875} = 0.2857 \),
- \( w_2 = \frac{0.25}{0.875} = 0.2857 \),
- \( w_{new} = \frac{0.375}{0.875} = 0.4286 \).
#### Adding Another Shard:
Repeat the process with \( n = 3 \), and so on.
---
### Conclusion
This approach ensures that new shards receive a higher weight initially, but as more shards are added, the weights converge to uniformity. The key is using a weight formula that decreases the bias dynamically as the system grows. Let me know if you have further questions!