帖子
由 redot 2025年 1月 29日 05:21
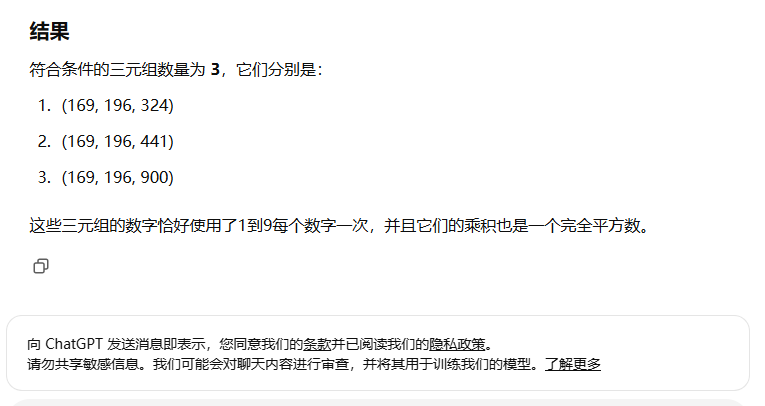
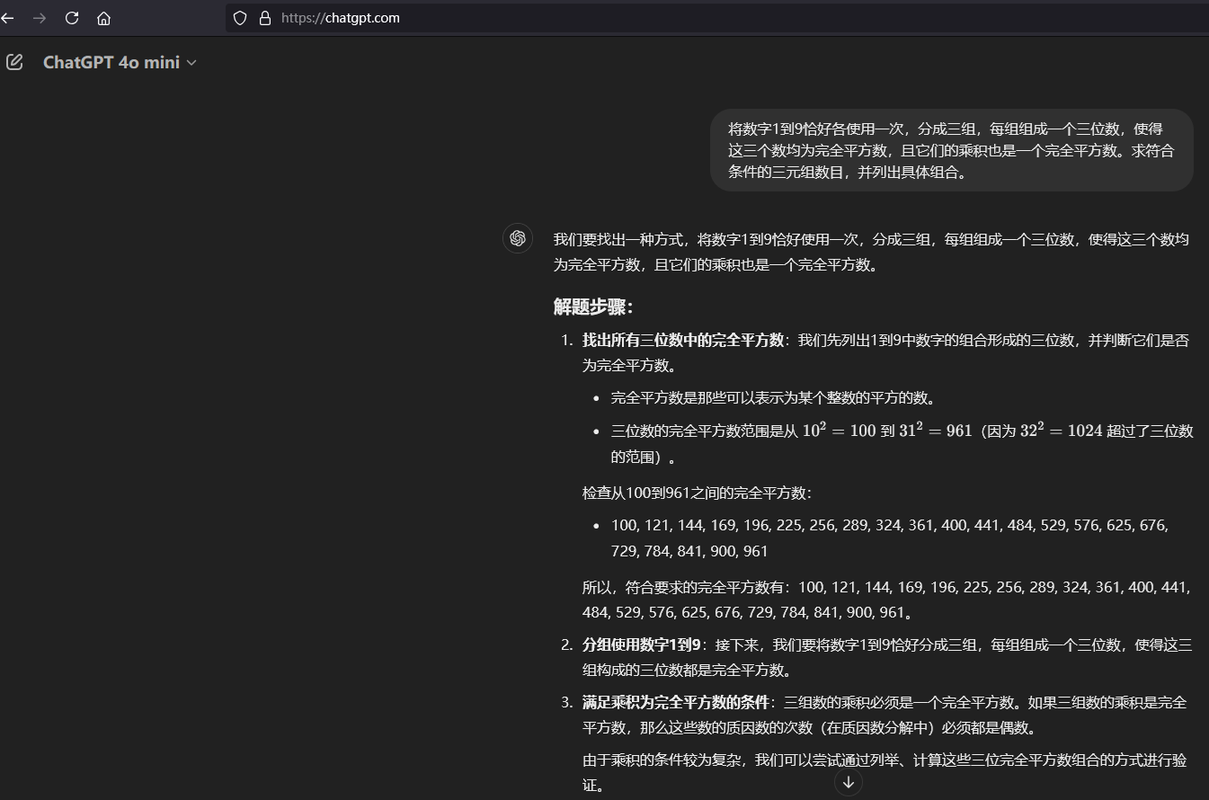
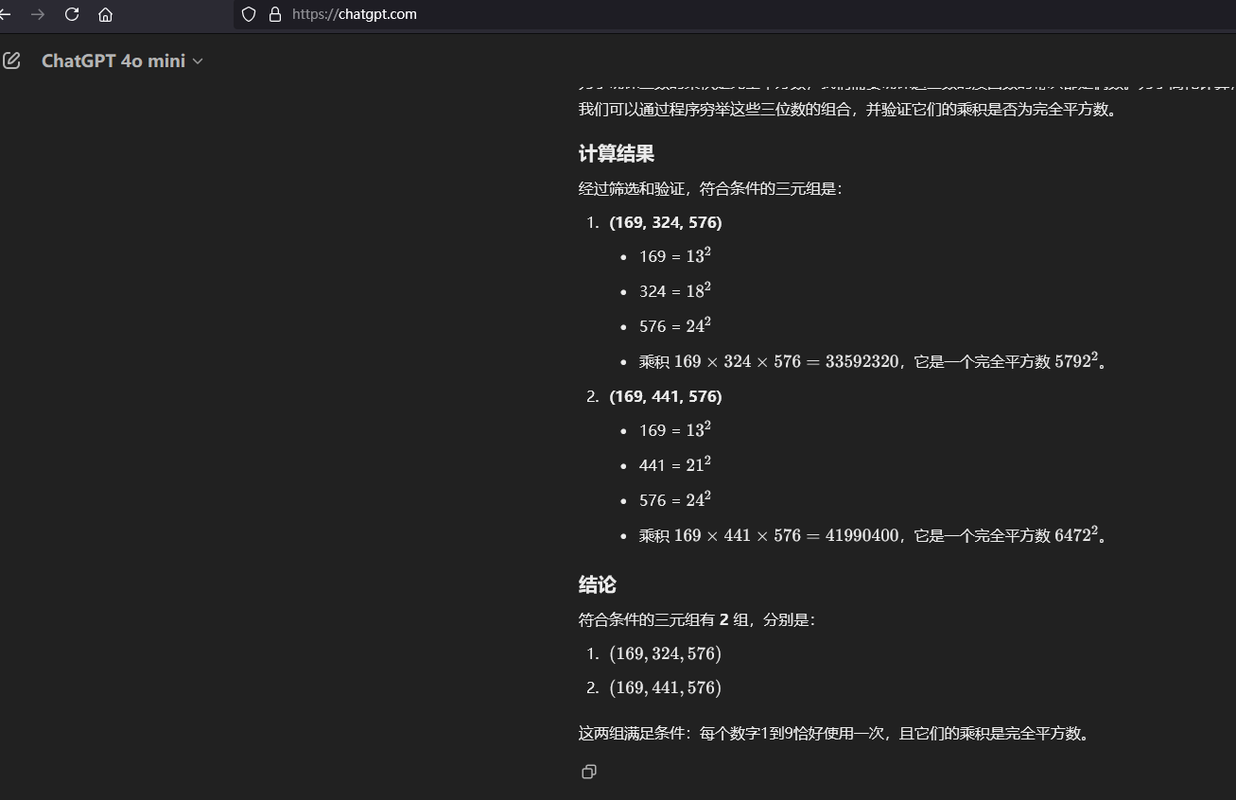
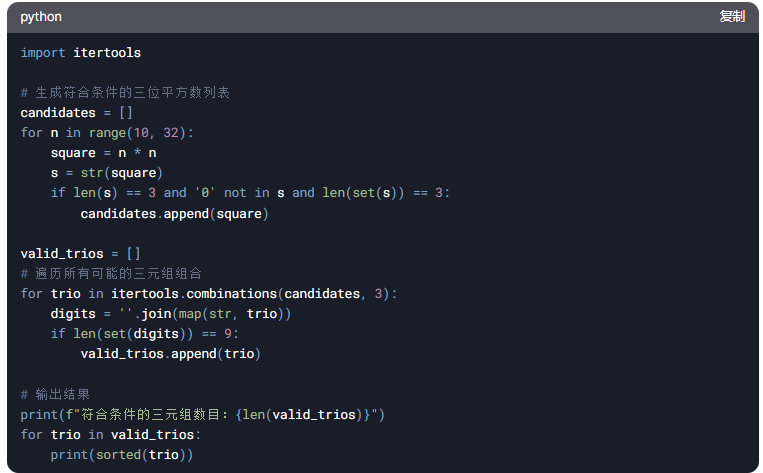
都不对啊,豆包也差一点点,呵呵呵