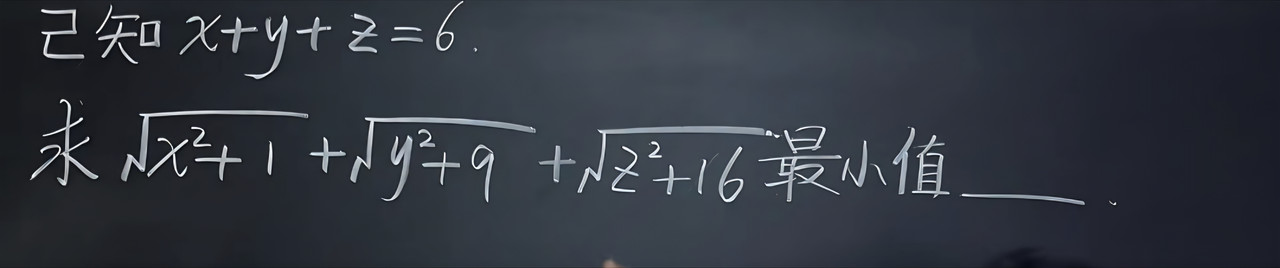
陈立人小时候做过的数学题，mit会做的不超过五个
版主： Softfist
#5 Re: 陈立人小时候做过的数学题，mit会做的不超过五个
不知道能否把Z变成X和Y的组合，代进去。既然在约束的多平面里取值，代入后的函数极值点对X和Y的偏导应该为零，得到二元一次方程组，解方程得到极值点。
-
juderiverman（兄弟是朱德）
- 论坛点评
juderiverman 的博客 - 帖子互动： 211
- 帖子： 3063
- 注册时间： 2022年 9月 28日 08:36
#7 Re: 陈立人小时候做过的数学题，mit会做的不超过五个
6,0,0……sqrt(37)+3+4=13.0828
4,1,1……sqrt(17)+sqrt(10)+sqrt(17)=11.408
1,1,4……sqrt(2)+sqrt(10)+sqrt(32)=10.233
1,2,3….sqrt(2)+sqrt(13)+sqrt(25)=10.0198
上次由 juderiverman 在 2025年 6月 26日 23:12 修改。
“We achieve inner peace when our schedule aligns with our values.”
#12 Re: 陈立人小时候做过的数学题，mit会做的不超过五个
提示: 数形结合，勾股定理juderiverman 写了： 2025年 6月 26日 22:52 6,0,0……sqrt(37)+3+4=13.0828
4,1,1……sqrt(17)+sqrt(10)+sqrt(17)=11.408
1,1,4……sqrt(2)+sqrt(10)+sqrt(32)=10.233
1,2,3….sqrt(2)+sqrt(13)+sqrt(25)=10.0198
#13 Re: 陈立人小时候做过的数学题，mit会做的不超过五个
The expression to minimize is sqrt(x² + 1²) + sqrt(y² + 3²) + sqrt(z² + 4²).
Each term in the sum can be interpreted as the length of the hypotenuse of a right triangle, or as the distance between two points in a 2D plane.
Let's visualize this as the length of a path made of three segments:
A segment with a horizontal displacement of x and a vertical displacement of 1. Its length is sqrt(x² + 1²).
A segment with a horizontal displacement of y and a vertical displacement of 3. Its length is sqrt(y² + 3²).
A segment with a horizontal displacement of z and a vertical displacement of 4. Its length is sqrt(z² + 4²).
The total length of this path is the sum we want to minimize. The path starts at an origin point, say (0,0), and ends at the point whose coordinates are the sum of the displacements.
The total horizontal displacement is x + y + z.
The total vertical displacement is 1 + 3 + 4 = 8.
We are given the constraint that x + y + z = 6. Therefore, the path connects the starting point (0, 0) to the fixed endpoint (6, 8).
The sum of the lengths of the path segments is minimized when the path is a straight line. The minimum value of the expression is therefore the straight-line distance between the point (0, 0) and the point (6, 8).
We can calculate this distance using the distance formula:
Distance = sqrt((6 - 0)² + (8 - 0)²)
Distance = sqrt(6² + 8²)
Distance = sqrt(36 + 64)
Distance = sqrt(100)
Distance = 10
Thus, the smallest possible value of the expression is 10.
看看gemini多牛逼
Each term in the sum can be interpreted as the length of the hypotenuse of a right triangle, or as the distance between two points in a 2D plane.
Let's visualize this as the length of a path made of three segments:
A segment with a horizontal displacement of x and a vertical displacement of 1. Its length is sqrt(x² + 1²).
A segment with a horizontal displacement of y and a vertical displacement of 3. Its length is sqrt(y² + 3²).
A segment with a horizontal displacement of z and a vertical displacement of 4. Its length is sqrt(z² + 4²).
The total length of this path is the sum we want to minimize. The path starts at an origin point, say (0,0), and ends at the point whose coordinates are the sum of the displacements.
The total horizontal displacement is x + y + z.
The total vertical displacement is 1 + 3 + 4 = 8.
We are given the constraint that x + y + z = 6. Therefore, the path connects the starting point (0, 0) to the fixed endpoint (6, 8).
The sum of the lengths of the path segments is minimized when the path is a straight line. The minimum value of the expression is therefore the straight-line distance between the point (0, 0) and the point (6, 8).
We can calculate this distance using the distance formula:
Distance = sqrt((6 - 0)² + (8 - 0)²)
Distance = sqrt(6² + 8²)
Distance = sqrt(36 + 64)
Distance = sqrt(100)
Distance = 10
Thus, the smallest possible value of the expression is 10.
看看gemini多牛逼
x1
宽衣，通商，唐诗，宋词，秦刚，秦城
此生不悔入华夏，来世还做小昂萨
此生不悔入华夏，来世还做小昂萨
-
juderiverman（兄弟是朱德）
- 论坛点评
juderiverman 的博客 - 帖子互动： 211
- 帖子： 3063
- 注册时间： 2022年 9月 28日 08:36
#15 Re: 陈立人小时候做过的数学题，mit会做的不超过五个
加整数条件，并更改总和为8，请试图直接说出答案：
X+y+z=8
X,y,z are integrals
Min(sqrt(x^2+1)+sqrt(y^2+9)+sqrt(z^2+16))
X+y+z=8
X,y,z are integrals
Min(sqrt(x^2+1)+sqrt(y^2+9)+sqrt(z^2+16))
“We achieve inner peace when our schedule aligns with our values.”
#16 Re: 陈立人小时候做过的数学题，mit会做的不超过五个
构建一个直角边分别与x轴和y轴平行的直角三角形，斜边的一端是原点，另一端的坐标是(x,1), 该直角三角形的斜边长度为sqrt(x**2 + 1);
再构建一个直角边分别与x轴和y轴平行的直角三角形，斜边的一端的坐标是(x,1)，另一端的坐标是(x + y, 4), 该直角三角形的斜边长度为sqrt(y**2 + 9);
再构建一个直角边分别与x轴和y轴平行的直角三角形，斜边的一端的坐标是(x + y, 4)，另一端的坐标是(x + y + z, 8), 该直角三角形的斜边长度为sqrt(z**2 + 16);
注意x+y+z = 6, 故最后一点的坐标为(6, 8). 另注意题目中需要最小化的变量为三条斜边之和。于是，最小值为原点到(6,8)的距离，即10。
再构建一个直角边分别与x轴和y轴平行的直角三角形，斜边的一端的坐标是(x,1)，另一端的坐标是(x + y, 4), 该直角三角形的斜边长度为sqrt(y**2 + 9);
再构建一个直角边分别与x轴和y轴平行的直角三角形，斜边的一端的坐标是(x + y, 4)，另一端的坐标是(x + y + z, 8), 该直角三角形的斜边长度为sqrt(z**2 + 16);
注意x+y+z = 6, 故最后一点的坐标为(6, 8). 另注意题目中需要最小化的变量为三条斜边之和。于是，最小值为原点到(6,8)的距离，即10。
#20 Re: 陈立人小时候做过的数学题，mit会做的不超过五个
先学好英文吧，啥叫“X,y,z are integrals”？Try understand the difference between integer and integral.
juderiverman 写了： 2025年 6月 26日 23:17 加整数条件，并更改总和为8，请试图直接说出答案：
X+y+z=8
X,y,z are integrals
Min(sqrt(x^2+1)+sqrt(y^2+9)+sqrt(z^2+16))