又有大证明了 - 计算机辅助证明 - preprint - 流体力学Euler方程 blow up了 - Fefferman有评论

[atman]

所以说其实N-S方程其实是不正确的，有热参与，机械能不守恒。

大哥，机械能守恒是伯努利方程，不是ns

[jiujianoufu]

搞笑，当然存在

恕我孤陋寡闻，烦请找一个现实存在的欧拉流体出来，让大家开开眼.

[atman]

搞笑，当然存在

超流体？

[弃婴千枝]

4He-II

non viscous, non compressible

还有quark matter，quark gluon matter

恕我孤陋寡闻，烦请找一个现实存在的欧拉流体出来，让大家开开眼.

[wsnren]

https://www.quantamagazine.org/computer ... -20221116/

Perhaps the oldest and most prominent of these equations, formulated by Leonhard Euler more than 250 years ago, describe the flow of an ideal, incompressible fluid: a fluid with no viscosity, or internal friction, that cannot be forced into a smaller volume. “Almost all nonlinear fluid equations are kind of derived from the Euler equations,” said Tarek Elgindi, a mathematician at Duke University. “They’re the first ones, you could say.”

https://arxiv.org/abs/2210.07191

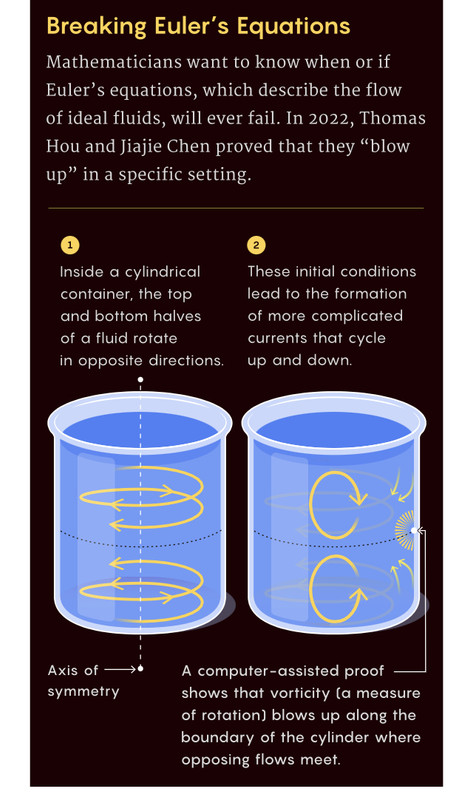
In a preprint posted online last month, a pair of mathematicians has shown that a particular version of the Euler equations does indeed sometimes fail. The proof marks a major breakthrough — and while it doesn’t completely solve the problem for the more general version of the equations, it offers hope that such a solution is finally within reach. “It’s an amazing result,” said Tristan Buckmaster, a mathematician at the University of Maryland who was not involved in the work. “There are no results of its kind in the literature.”

The 177-page proof — the result of a decade-long research program — makes significant use of computers. This arguably makes it difficult for other mathematicians to verify it. (In fact, they are still in the process of doing so, though many experts believe the new work will turn out to be correct.) It also forces them to reckon with philosophical questions about what a “proof” is, and what it will mean if the only viable way to solve such important questions going forward is with the help of computers.

To get the tight bounds they needed on all these different terms, Hou and Chen broke the inequality into two major parts. They could take care of the first part by hand, with techniques including one that dates back to the 18th century, when the French mathematician Gaspard Monge sought an optimal way of transporting soil to build fortifications for Napoleon’s army. “Stuff like this has been done before, but I found it striking that [Hou and Chen] used it for this,” Fefferman said.

That left the second part of the inequality. Tackling it would require computer assistance. For starters, there were so many calculations that needed to be done, and so much precision required, that “the amount of work you’d have to do with pencil and paper would be staggering,” de la Llave said. To get various terms to balance out, the mathematicians had to perform a series of optimization problems that are relatively easy for computers but exceedingly time-consuming for humans. Some of the values also depended on quantities from the approximate solution; since that was calculated using a computer, it was more straightforward to also use a computer to perform these additional computations.

不懂。但问了一个做方程的牛逼人物，他说侯一钊这工作很牛逼。

[jiujianoufu]

4He-II

non viscous, non compressible

这种流体是人造流体，而且成本很高。在自然界是显然不存在的。

[弃婴千枝]

存在，比如quark matter

这种流体是人造流体，而且成本很高。在自然界是显然不存在的。

[Caravel]

4He-II

non viscous, non compressible

还有quark matter，quark gluon matter

超流体不是有更复杂的物理么

[shenhaixiong]

继能教授之后，码工又砸了千老的饭碗？

[island]

数学意义还是很重要的，不过似乎也仅有数学意义。

fluid mechanics were divided into hydraulic engineers who observed things that could not be explained and mathematicians
who explained things that could not be observed. - Cyril Norman Hinshelwood

欧拉方程描绘无粘性和不可压缩流体，而这种流体在自然界是不存在的。这种脑残文章也能写177页？

[beijingren3]

不懂。但问了一个做方程的牛逼人物，他说侯一钊这工作很牛逼。

没啥牛逼的，都是建立在不同的假设上。连续介质力学应用有限。按理论，你在美国拍一巴掌，北京应该有感应。LOL

[beijingren3]

4He-II

non viscous, non compressible

还有quark matter，quark gluon matter

non viscous means， 你泼一杯水，瞬间杯子上不留下一颗水分子。LOL

[newIdRobot]

Mark

[弃婴千枝]

对

这世界很复杂，远远超过你的想象力

比如中子星内部，现在普遍认可是这样的

https://astrobites.org/2017/12/11/flux- ... r-mixture/

non viscous means， 你泼一杯水，瞬间杯子上不留下一颗水分子。LOL

[hhcare]

对

这世界很复杂，远远超过你的想象力

比如中子星内部，现在普遍认可是这样的

https://astrobites.org/2017/12/11/flux- ... r-mixture/

你还不如贴一段西游记。。。更让人信服。


I am an astrophysics PhD student with interests in compact objects and gravitational waves. I studied neutron star interiors for my Masters thesis at the University of Melbourne, Australia and now I am doing my PhD at MIT.

[rockyliu]

也就是说Euler方程的强解可能不存在。以前证明了弱解是存在的。连续介质物理是不支持弱解的。这个工作佐证了连续介质物理的局限性。也就是说连续介质物理需要有一个耗散系统才能自洽。也就是粘性项，热传导，或者其他。

[TheMatrix2]

也就是说Euler方程的强解可能不存在。以前证明了弱解是存在的。连续介质物理是不支持弱解的。这个工作佐证了连续介质物理的局限性。也就是说连续介质物理需要有一个耗散系统才能自洽。也就是粘性项，热传导，或者其他。

"以前证明了弱解是存在的。连续介质物理是不支持弱解的" - 写错了？

[TheMatrix2]

弱解可能是不连续的，与方程的连续假设抵触。
这个结果说明解释流体只靠连续性假设的偏微分方程不靠谱。
以前是个宗教问题，没人说服对方。
这个从最简单的情况说明了，很多事情都要改变。

弱解可以是不连续的。但是连续介质要求解必须是连续的，也就是不能是弱解。以前证明了弱解可以存在。但是如果假设连续介质的话，这个弱解存在就不够了。是这个意思吧？

[wttw]

这两位都学傻了吧，怎么不说分子的范德华力、万有引力、引力的量子效应统统都还没有考虑进去？

物理学的任何模型都是对真实世界的近似。是不是对任何模型解不解都没多大意思？

属实

更要命的是，实际过程还涉及热力学，不但有热传导，还有相变，更是复杂
属实

更要命的是，实际过程还涉及热力学，不但有热传导，还有相变，更是复杂
wwwhu 写了： ↑昨天, 11:54 pm
数学家自娱自乐，物理学家目瞪口呆。
理想流体不存在。
N-S方程本身就是三个守恒律的总和，连粘度都没有的玩意，正确无比，解不解有多大意思？

[wttw]

五个质点的万有引力方程也会blow up.
任何模型都有可能blow up，但不妨碍在远离blow up情形的使用。知道什么情况会blow up很重要。现在我们进一步知道欧拉方程一些情况会blow up了，意义非常重大。

也就是说Euler方程的强解可能不存在。以前证明了弱解是存在的。连续介质物理是不支持弱解的。这个工作佐证了连续介质物理的局限性。也就是说连续介质物理需要有一个耗散系统才能自洽。也就是粘性项，热传导，或者其他。