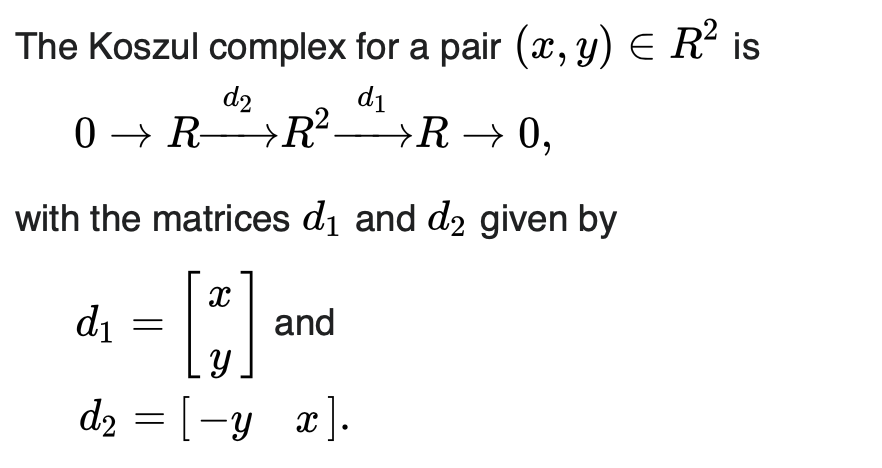Galois cohomology

[三农]

这个是我问Gemini，它给我的视频链接。

Snake lemma我很早就学过，但是从来没有认真chase diagram过一次。

这个Youtuber 我还看过她不少视频，好像以前是 Chicago 的Ph.D. 学生。有不少关于数论的内容。

[TheMatrix]

赞专业精神

拜读了，知道为啥要搞restriction/inflation这些东东了。

“K上有解，K_v上一定有解。”这是肯定的，因为前者被后者包含。不肯定的是，如果在所有K_v上有解，在K上是否有解？

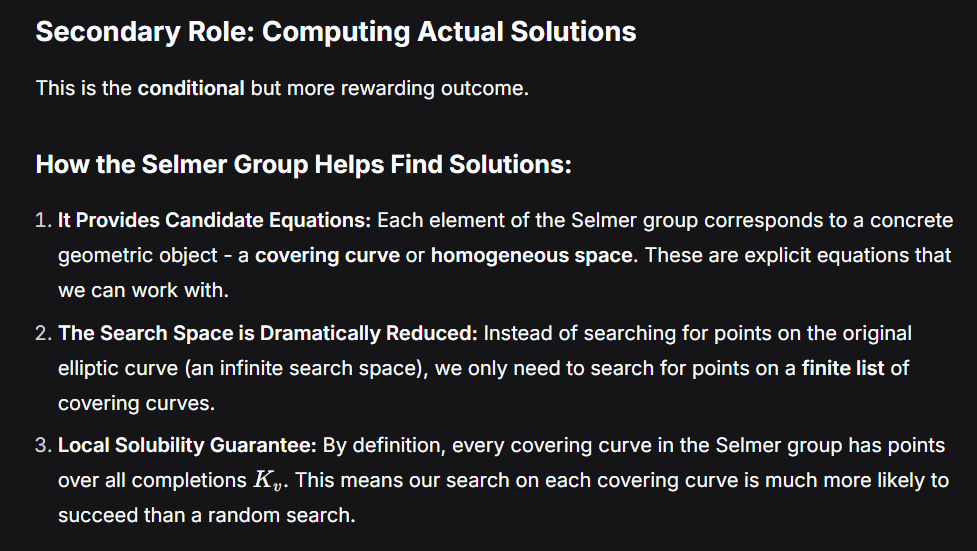
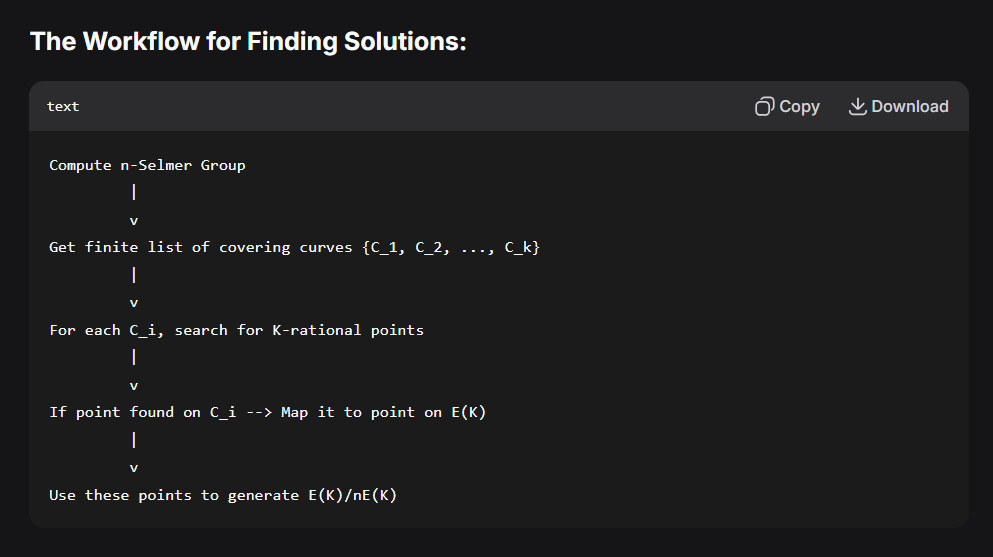
问题是Selmer，山群是干啥用的？代表了什么？

我问了一下deepseek，感觉是：Selmer group对计算椭圆曲线有直接的帮助。山群好像只有理论意义。

[FoxMe]

学海无涯苦作舟 应该说现在有AI，已经幸福多了。

我问了一下deepseek，感觉是：Selmer group对计算椭圆曲线有直接的帮助。山群好像只有理论意义。

[FoxMe]

Koszul complex为啥要外积？和我们以前讨论的standard complex差不多

https://en.wikipedia.org/wiki/Koszul_co ... Definition

但是这个例子又没那么复杂：

[三农]

Koszul complex为啥要外积？和我们以前讨论的standard complex差不多

https://en.wikipedia.org/wiki/Koszul_co ... Definition

但是这个例子又没那么复杂：

只有外积才能给出chain complex, 这就像 最开始定义simplicial homology 时，必需有 符号。对一个三角形【123】，

boundary （【123】）=【23】-【13】+【12】，

对应的，de Rham cohomology 用外微分形式，只有这样才能 定义 d: Omega^r(M) -> Omega^{r+1}(M), 这样定义了一个cochain complex，而且不依赖于 坐标系的选取。

第二个例子只是定义的特例，不过第一个map 也有可能是 (y, -x).

这些Koszul complex 好像在 交换代数 里很有用，给出 Cohen-Macaulay 之类的东西，那些我也只是在看。