Galois group representation

[TheMatrix]

可以这样看：

假设有一个modular form f，我们要对它做一些操作，这个操作必须是容易在傅里叶系数上实现的。

start with f(pz)。这个傅里叶系数上很容易操作的。

但是它不modular。它不modular with respect to the full modular group SL(2,Z)。它modular with respect to a subgroup of the modular group。那也不行，我们要求它必须modular with respect to the full modular group SL(2,Z)。

也就是看它到底哪里不modular。

用T和S来作用它。

T作用它，等于 f(pTz)=f(p(z+1))=f(pz+p)=f(pz)。所以在T下modular。虽然它的周期拉长了。

S作用它，等于 f(pSz)=f(-p/z)=f(S.(z/p))=(z/p)^kf(z/p)。

出来了一个新的东西 f(z/p)。把它包含进去，希望能闭环。

有它就要有 f(Tz/p)，也就是f((z+1)/p)。这又是一个新的东西。

再做T，f(TTz/p)，就是 f((z+2)/p)。。。一直做到 f((z+p-1)/p)，再做就循环了。

所以这就是全部。。。对T是全部。

然后还要对S闭环。。。这里正好是已经对S闭环了。也许可以对S不闭环，那就需要对S进行扩展。

也就是对S和T交替扩展直至闭环。

然后还要拼凑系数。

这样就得到一个新的modular form。。。的产生方式。

用S和T也是因为它们在傅里叶系数上是很容易操作的。

[TheMatrix]

第一项对应：
a₀+a₁q^p+a₂q^2p+a₃q^3p+...

第二项对应：
a₀+a_pq+a_2pq²+a_3pq³+...

其他的a_n项被互相cancel掉了。

所以可以写成
Σ_n p^k-1a_nq^np+a_npqⁿ

再用这个证明 T_pT_q = T_qT_p。

这个属于index tracking，也不容易。

也就是如果modular form f的傅里叶系数是a(n)，那么 T_qT_pf的傅里叶系数是什么的问题。

写成a(n) instead of a_n是为了后面代入，这里实际上是function composition，用下标会很困扰。

T_pf的傅里叶系数为b(n)：
b(n)=a(np) when n != 0 mod p
b(n)=p^k-1a(n/p)+a(np) when n = 0 mod p

这个公式同样适用于q。

然后是T_qT_pf的傅里叶系数为 c(n)：
c(n)=b(nq) when n != 0 mod q
c(n)=q^k-1b(n/q)+b(nq) when n = 0 mod q

这样就可以把b(n)的表达式代入进去。用下标写的话就很难了。

代入进去就很容易发现，p和q的顺序不影响傅里叶系数。所以就有了T_pT_q = T_qT_p。

因此就有了Hecke operator T_n对任意正整数n的定义。

[TheMatrix]

再用这个证明 T_pT_q = T_qT_p。

这个属于index tracking，也不容易。

也就是如果modular form f的傅里叶系数是a(n)，那么 T_qT_pf的傅里叶系数是什么的问题。

写成a(n) instead of a_n是为了后面代入，这里实际上是function composition，用下标会很困扰。

T_pf的傅里叶系数为b(n)：
b(n)=a(np) when n != 0 mod p
b(n)=p^k-1a(n/p)+a(np) when n = 0 mod p

这个公式同样适用于q。

然后是T_qT_pf的傅里叶系数为 c(n)：
c(n)=b(nq) when n != 0 mod q
c(n)=q^k-1b(n/q)+b(nq) when n = 0 mod q

这样就可以把b(n)的表达式代入进去。用下标写的话就很难了。

代入进去就很容易发现，p和q的顺序不影响傅里叶系数。所以就有了T_pT_q = T_qT_p。

因此就有了Hecke operator T_n对任意正整数n的定义。

Hecke operator T_n的定义有了。

接下来可以把T_n的定义以表达式的方式写出来，还可以写出T_nf对傅里叶系数的变换规则。

也可以先不管它们，直接看Hecke operator的eigenvalue和eigenform，也就是eigenvector。

[TheMatrix]

先在周围扫荡一下。



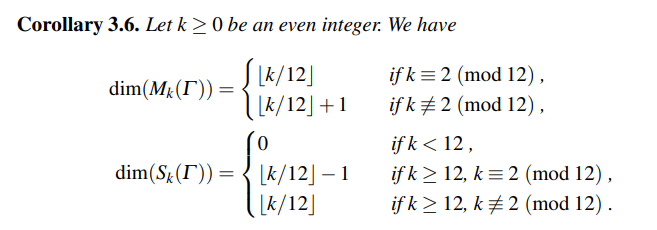
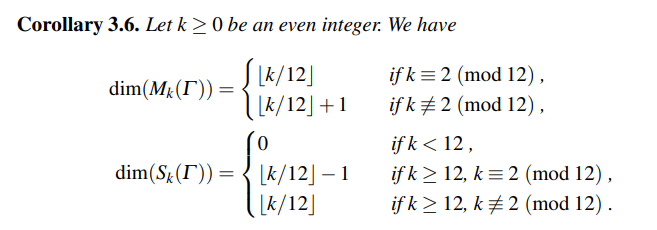
看来modular form是很小的空间。weight k比较小的时候，基本上只有一个modular form，那就是Eisenstein series。

比如weight k < 12，只有Eisenstein series：E₄,E₆,E₈,E₁₀。而Eisenstein series傅里叶系数首项都不是0，所以都不是cusp form。也就是没有cusp form。

weight k >= 12的时候，cusp form的dimension等于modular form的dimension -1。也就是只有一个不是cusp form的modular form，那就只能是Eisenstein series。

k继续往上走的时候，cusp form继续增加，而不是cusp form的modular form还是只有Eisenstein series一个。

[TheMatrix]

[TheMatrix]

Eisenstein series通常用G_2k表示。而E_2k是去掉ζ factor之后的量。

去掉ζ，再去掉和Bernoulli有关的系数，Eisenstein傅里叶系数基本上是σ。

这是一个数论函数。也就是整数到整数的函数。

σ(n)就是n的全部因子的和。
σ₃(n)是n的全部因子的立方和。
....


难怪modular form和数论有关，这完全就是数论啊！

而且它除了数论也基本上没别的了。因为Eisenstein series是唯一的一个不是cusp的modular form。

Cusp form的维度在增加。但应该也都是和数论有关的。

[TheMatrix]

[TheMatrix]

我前面说the space of modular form是一个algebra，这是错的。因为不同weight的modular form是不能相加的。

这里的M_*不是the space of modular form。而是the direct sum of the space of weight-k modular form。所以不是元素直接相加，而是direct sum相加。加出来不再是一个函数了。

[TheMatrix]

我前面说the space of modular form是一个algebra，这是错的。因为不同weight的modular form是不能相加的。

这里的M_*不是the space of modular form。而是the direct sum of the space of weight-k modular form。所以不是元素直接相加，而是direct sum相加。加出来不再是一个函数了。

direct sum也可以看成是一个函数，就是直接相加的函数。但这个函数就不再是modular form了。

也就是要扩大到H上的解析函数的空间上看了。也就是M_*是这个空间的一部分。

[TheMatrix]

据说这个是用Riemann-Roch定理证明的。好像也可以不用。据说比较简单。

Riemann-Roch需要理解一下。

[TheMatrix]

也就是说M_*这个函数空间，是由G₄和G₆生成的。也就是G₄和G₆的polynomial。而其中的齐次项为modular form。

S_*是cusp form space的direct sum。它是一个subalgebra。而它还是一个ideal。而且是principal ideal。它的generator是Δ。

Δ=c(G₄³-G₆²)

这都不是很trivial。

[TheMatrix]

也就是说M_*这个函数空间，是由G₄和G₆生成的。也就是G₄和G₆的polynomial。而其中的齐次项为modular form。

S_*是cusp form space的direct sum。它是一个subalgebra。而它还是一个ideal。而且是principal ideal。它的generator是Δ。

Δ=c(G₄³-G₆²)

这都不是很trivial。

Δ的傅里叶系数是τ(n)：



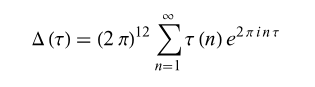
τ(n)的前几个数是：
1, -24, 252, -1472, 4830, -6048, -16744, 84480, -113643, -115920, 534612, -370944, -577738, 401856, 1217160, 987136, -6905934, 2727432, 10661420, -7109760, -4219488, -12830688, 18643272, 21288960, -25499225, 13865712, -73279080, 24647168

Δ是Hecke operator的eigenform，也就是eigenvector。

也就是Δ和T_nΔ的傅里叶系数相同 - 提出一个常数之后。

[TheMatrix]

Δ的傅里叶系数是τ(n)：



τ(n)的前几个数是：
1, -24, 252, -1472, 4830, -6048, -16744, 84480, -113643, -115920, 534612, -370944, -577738, 401856, 1217160, 987136, -6905934, 2727432, 10661420, -7109760, -4219488, -12830688, 18643272, 21288960, -25499225, 13865712, -73279080, 24647168

Δ是Hecke operator的eigenform，也就是eigenvector。

也就是Δ和T_nΔ的傅里叶系数相同 - 提出一个常数之后。

Hecke operator T_p 当 p 为素数时，对傅里叶系数的变换比较简单：

f的傅里叶系数为a(n)，那么T_pf的傅里叶系数b(n)
= a(np) 如果 n 不能整除 p
= a(np) + p^k-1 a(n/p) 如果n能整除p

比如p=5，k=12 （Δ的weight）
n=1，那么b(1)=a(5)
n=2，那么b(2)=a(10)
n=3，那么b(3)=a(15)
n=4，那么b(4)=a(20)
n=5，那么b(5)=a(20)+5¹¹ a(1)
n=6，那么b(6)=a(30)
n=7，那么b(7)=a(35)
n=8，那么b(8)=a(40)
n=9，那么b(9)=a(45)
n=10，那么b(10)=a(50)+5¹¹ a(2)
....

b(n)/a(n)就是T₅的eigenvalue。

这个规律确实成立。

而且还可以T₂，T₃，...

这个规律也对Δ的傅里叶系数有很强的限制。肯定是可以递推的。

[TheMatrix]

Hecke operator T_p 当 p 为素数时，对傅里叶系数的变换比较简单：

f的傅里叶系数为a(n)，那么T_pf的傅里叶系数b(n)
= a(np) 如果 n 不能整除 p
= a(np) + p^k-1 a(n/p) 如果n能整除p

比如p=5，k=12 （Δ的weight）
n=1，那么b(1)=a(5)
n=2，那么b(2)=a(10)
n=3，那么b(3)=a(15)
n=4，那么b(4)=a(20)
n=5，那么b(5)=a(20)+5¹¹ a(1)
n=6，那么b(6)=a(30)
n=7，那么b(7)=a(35)
n=8，那么b(8)=a(40)
n=9，那么b(9)=a(45)
n=10，那么b(10)=a(50)+5¹¹ a(2)
....

b(n)/a(n)就是T₅的eigenvalue。

这个规律确实成立。

而且还可以T₂，T₃，...

这个规律也对Δ的傅里叶系数有很强的限制。肯定是可以递推的。

傅里叶系数是整数，这本身就很神奇！

一般来讲，傅里叶的两边，规律很难沟通。

f作为函数的规律，和傅里叶变换后(a₀,a₁,a₂,...)数列的规律。这两边很难同时有规律。

这就是傅里叶的一大主题。

[TheMatrix]

Δ的傅里叶系数是τ(n)：



τ(n)的前几个数是：
1, -24, 252, -1472, 4830, -6048, -16744, 84480, -113643, -115920, 534612, -370944, -577738, 401856, 1217160, 987136, -6905934, 2727432, 10661420, -7109760, -4219488, -12830688, 18643272, 21288960, -25499225, 13865712, -73279080, 24647168

Δ是Hecke operator的eigenform，也就是eigenvector。

也就是Δ和T_nΔ的傅里叶系数相同 - 提出一个常数之后。

我们为什么知道Δ是Hecke operator的eigenform？

因为Δ等于c(E₄³-E₆²)，是一个weight-12 cusp form。而weight-12 cusp form space根据公式只有一维。所以Δ其实是唯一的weight-12 cusp form。所以它必须是Hecke operator的eigenform。

[TheMatrix]

Hecke operator T_p 当 p 为素数时，对傅里叶系数的变换比较简单：

f的傅里叶系数为a(n)，那么T_pf的傅里叶系数b(n)
= a(np) 如果 n 不能整除 p
= a(np) + p^k-1 a(n/p) 如果n能整除p

比如p=5，k=12 （Δ的weight）
n=1，那么b(1)=a(5)
n=2，那么b(2)=a(10)
n=3，那么b(3)=a(15)
n=4，那么b(4)=a(20)
n=5，那么b(5)=a(20)+5¹¹ a(1)
n=6，那么b(6)=a(30)
n=7，那么b(7)=a(35)
n=8，那么b(8)=a(40)
n=9，那么b(9)=a(45)
n=10，那么b(10)=a(50)+5¹¹ a(2)
....

b(n)/a(n)就是T₅的eigenvalue。

这个规律确实成立。

而且还可以T₂，T₃，...

这个规律也对Δ的傅里叶系数有很强的限制。肯定是可以递推的。

假设知道Δ的傅里叶系数第一项和第p项，a(1)和a(p)，p为素数。

用Hecke operator T_p作用在Δ上，假设其傅里叶系数为b(n)。

那么，
b(1) = a(p)，而λ=b(1)/a(1)=a(p)/a(1)就是 T_p 的eigenvalue。
b(p) = λa(p) = a(p²)+p¹¹a(1)，可以推出a(p²)。
b(p²) = λa(p²) = a(p³)+p¹¹a(p)，可以推出a(p³)。
....

这样就能推出所有a(pⁿ)傅里叶系数。

所以还是要知道Δ在所有素数位置的傅里叶系数。

[FoxMe]

现在研究数论问题，需要modular/automorphic form

[TheMatrix]

据说这个是用Riemann-Roch定理证明的。好像也可以不用。据说比较简单。

Riemann-Roch需要理解一下。

没用Riemann-Roch。用的是这个定理。这个定理用了对 f'/f 的积分。据说比较简单：



感觉不是很简单。

[TheMatrix]

没用Riemann-Roch。用的是这个定理。这个定理用了对 f'/f 的积分。据说比较简单：



感觉不是很简单。

没有证明。然后就说很容易推出下面这两个 - 感觉也不是很容易：

[TheMatrix]

没用Riemann-Roch。用的是这个定理。这个定理用了对 f'/f 的积分。据说比较简单：



感觉不是很简单。

求和要make sense要求f在fundamental domain里只有有限个零点。这是对的。

应该要用留数定理。再去复习一下。